AHA!基于决策的黑盒模型的自适应历史驱动攻击
Aha! Adaptive History-driven Attack for Decision-based Black-box Models

ABSTRACT

基于决策的黑盒攻击指的是只使用受害者模型的前1个标签来制作对抗示例。一种常见的做法是从一个大的扰动开始，然后用一个确定的方向和一个随机的方向迭代地减少它，同时保持它的对抗性。从每个查询中获得的有限信息和低效的方向采样阻碍了攻击效率，使得在有限的查询数量中很难获得足够小的扰动。为了解决这一问题，我们提出了一种新的攻击方法，称为自适应历史驱动攻击(AHA)，它从所有历史查询中收集信息作为当前采样的先验。此外，为了平衡确定性方向和随机方向，我们根据实际减幅与预期减幅的比值动态调整系数。
这样的策略提高了优化过程中查询的成功率，使对抗性示例沿着决策边界快速移动。我们的方法还可以与降维等子空间优化相结合，进一步提高效率。在ImageNet和CelebA数据集上的大量实验表明，在相同的查询次数下，我们的方法获得的扰动幅度平均至少降低24.3%。最后，我们通过对流行的防御方法和MEGVII face++提供的一个真实系统进行评估，证明了我们的方法的实用潜力。

1. INTRODUCTION

随着深度神经网络(DNNs)的快速发展和主导性能，它已成功应用于许多领域，如智能音箱中的语音助手、云上的图像识别api和汽车自动驾驶等。尽管人们花了很多精力来解释dnn[1,18,19,43]，但dnn还远远不能完全可控，并且已被证明易受精心设计的不可感知扰动的影响，例如对抗性扰动[41]，这对dnn在安全场景中的应用构成了威胁。
因此，人们提出了许多方法来评估dnn在不同设置下的鲁棒性[13,4,21]。在所有的设置中，黑箱设置是最实用但最具挑战性的，因为只有相应的输出是可用的。一些攻击方法[29,38,37]在白盒模型上制作对抗实例，并将其转移到受害者模型。这些基于传输的方法消耗的资源较少，但不能保证高的攻击成功率。有些对手会反复查询模型。根据输出形式的不同，基于查询的黑盒攻击方法又可进一步分为基于分数的攻击和基于决策的攻击。前者的输出通常是连续的浮点数(如类概率)，能够快速响应输入的变化，从而引导微扰的逐级生成。基于决策的攻击设置更具挑战性，其中对手只能获取结果，不管输入是否属于与目标样本相同的类。这样的设置通常与目标攻击相关，目标攻击的目标是创建一个分类为目标的对抗示例。
最经典的基于决策的攻击是Boundary attack[2]，它从一个对敌的例子开始，沿着两个方向搜索:直接朝着源图像的源方向减少摄动，以及从正态分布中随机采样的球面方向进行探索。然而，该方法主要依赖随机抽样，没有有效利用先验查询的信息，导致查询数量巨大。人们提出了许多方法来改进它。偏置边界攻击[3]引入三种偏置来提高方向采样效率。进化攻击[10]减少了解决方案空间，并通过(1+1)- cmae优化的成功查询对局部几何进行建模。然而，这些方法没有充分利用所有查询的所有信息，仍然需要大量的查询来减少扰动的量级。此外，两个方向的取舍也有很大的影响。我们认为，减小扰动的方向系数越大，查询越边界而失败的次数就越多，而探索方向系数越大，查询次数就越多。现有的方法根据查询是否对抗性来调整相应的系数。这样的二元值给出了一个粗糙的指导，从而使系数调整不灵活。
在本文中，为了在更少的查询下获得更小的扰动，我们提出了自适应历史驱动攻击(AHA)，它利用所有查询的信息和自适应系数调整策略。在边界攻击之后，AHA从一个大的扰动开始，然后以一个确定的方向(即源方向)和一个随机的方向迭代地减小扰动。我们不是从随机方向的标准正态分布中随机抽样，而是从历史查询中收集信息，并将其作为当前抽样的先验。该方法简单有效，不增加额外的计算成本。为了在源方向和历史查询驱动方向之间取得平衡，考虑到系数调整的目的是尽可能减小扰动的大小，我们根据扰动大小的实际减少量与期望减少量的比值动态调整系数。这种策略减少了陷入决策边界的机会。此外，该优化方法与现有的降维等子空间方法是正交的。这些方法可以集成以进一步提高性能。我们在各种模型上进行了大量的实验，包括一个现实世界的在线系统，以证明所提出的AHA的效率。我们的贡献总结如下:

• 本文提出了一种简单而有效的基于决策的攻击方法，即自适应历史驱动攻击(AHA)，该方法利用成功和失败的历史查询信息作为当前采样的先验，无需进行复杂的优化和增加额外的计算成本。
• 为了在优化过程中平衡两个方向，我们设计了一种新的动态调整系数的策略。该系数不是根据优化成功的频率来调整，而是根据与预期值相比实际减少的程度来调整，这增加了找到有效查询的可能性。
• 最后，我们在自然图像和人脸模型上评估AHA。与相同查询次数的最先进方法相比，AHA产生的扰动更小。此外，AHA在现实系统(即MEGVII
  face++的人脸验证API)上的有效性也得到了验证，其扰动比基线小24.9%。

2.相关工作

略

3. 提出的方法

在整篇论文中，我们专注于在基于决策的目标黑盒攻击设置下减少有限查询内的扰动幅度。基于边界攻击，我们使用历史查询执行随机漫步优化，如第3.2节所述。两个搜索方向的系数对于更多地向源输入移动或更多地从历史中学习起着重要的作用。为了平衡它们，在3.3节中提出了一种新的自适应调整策略。可以借助3.4节中的子空间优化进一步改进优化方法。在本节的其余部分中，我们将首先介绍初步知识，然后对我们提出的方法进行全面描述。

3.1 预处理

假设我们有一个源输入样本x_s，一个目标样本x_t，一个基于深度神经网络的函数f(x1, x2): X × X →Y来判断两个输入样本是否属于同一类，其中X = [0,1]^d是d维图像的空间，Y ={0,1}(1表示两个输入共享同一类)。基于决策的目标攻击的目的是在保持f(x’, xt) = 1的情况下，寻找一个尽可能接近源输入xs的对抗示例x’。我们的目标函数为:

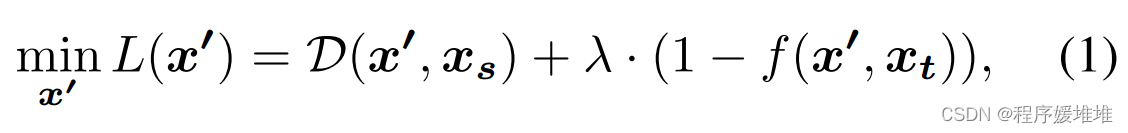
其中λ是一个非常大的数字，以确保当对抗目标不满足时L(x’)足够大，D(·，·)是距离函数。本文选取L2范数作为距离函数，即D(x’, xs) = ||x’−x_s||₂。

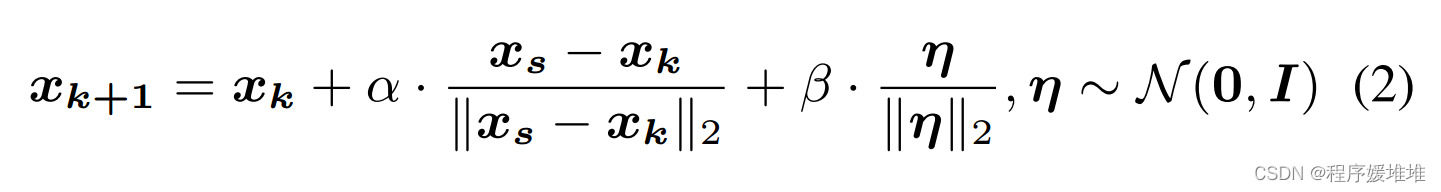
其中x_k为第k步的对抗例子，x_s为源输入，(x_s−x_k)和η分别为源方向和球方向。α和β是相应的系数。更新值可以进一步乘以当前样本与原始样本之间的距离，迭代地减小更新值，从而获得更好的收敛性:

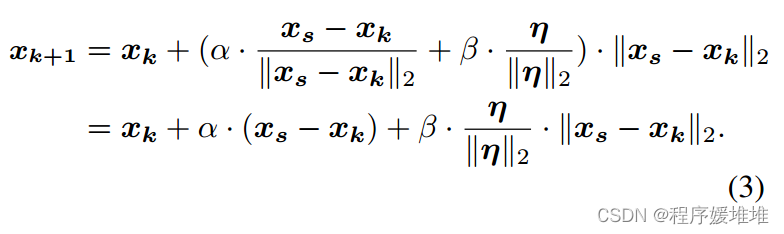
在这里，如果xk+1仍然是对抗性的，则称为成功的查询，否则称为失败的查询。
请注意，在之前的一些工作中，只有当L(x_k+1)小于或等于L(x_k)时，才会接受x_k+1，这是随机漫步优化中的常见做法。为了避免陷入局部最优，我们只拒绝不合格的样本。如果x_k+1被拒绝，那么为了便于表示，我们设x_k+1 = x_k。

3.2 基于历史先验的优化

仔细检查公式（3），唯一的不确定性在于随机方向，这极大地影响了优化方法的效率。以前的方法也在这方面做了努力。关键问题是如何使随机方向的采样更有效。已有研究证明，深度神经网络的决策边界在数据样本[12]附近具有相当小的曲率，这表明可以用超平面局部逼近对抗样例附近的决策边界[25,30]。由于边界是平坦的，我们可以自信地假设当前的随机方向与上一次迭代中的一个或更早的迭代在某种程度上是一致的。此外，之前也有一些研究表明，历史信息对当前采样是有帮助的[10,21,24,32]。但是，我们认为现有的利用历史先验的方法复杂且不彻底。例如，进化攻击[10]只利用成功的查询，而CAB[32]只利用失败的查询，而BanditsTD[21]利用所有查询，但不能很好地区分成功和失败的查询。
平坦的边界和缺乏充分利用历史信息促使我们使用更简单但更有效的方法来引导随机方向。如[2,10]所示，我们将历史先验视为自定义高斯分布。虽然分布的方差可以自然地模拟每个像素的重要性，但由于方差是独立的，不能很好地引导方向，因此修改方差也会引入不稳定性。我们关注的不是方差，而是分布的均值，并在其中嵌入成功和失败的历史查询信息。对于成功的查询x_k+1，其中f(x_k+1, x_t) = 1，如上所述，如果它们共享相似的方向，由于决策边界是平坦的，下一个方向将以高概率成功。而对于失败的查询，如[32]中所述，它还包含有关决策边界的信息，因为失败的查询穿过了该边界。与[32]类似，考虑其相反方向。特别地，我们用均值μ表示:

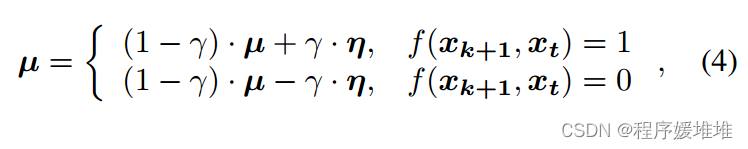
其中γ∈(0,1)是一个系数，用于控制忘记旧信息的速度，因为决策边界的几何属性将随着对抗示例的移动而变化。由于该方向是由历史查询驱动的，因此我们将其命名为历史驱动的方向。

3.4 系数自适应调整

另一个重要的问题是如何在来源方向和历史驱动方向之间取得平衡。较大的源方向系数α有助于快速减小扰动的大小，但它会增加到达决策边界的概率，从而导致查询失败。相反，较小的α会使优化方法更容易探索决策边界，但会减慢接近源输入的进度并增加查询次数。因此，需要一种自适应的调整策略。
以前的方法也注意到了这个问题，并为此付出了努力。边界攻击法在正交方向上选取更多的点来测试成功率，如果成功率较低，则减小系数，如果成功率接近50%或更高，则增大系数。偏向边界攻击在开始时使用较大的系数，并在失败查询数量增加时减小系数。当查询成功时，将重置系数。作为一种进化策略，进化方法利用了进化策略中超参数控制的传统方法，称为1/5成功规则[31]，通过乘以exp(P_success−1/5)来更新系数，其中P_success表示过去几次迭代的成功率。请注意，现有的方法都是基于成功率的，每个查询只能提供粗略的二进制反馈(即成功与否)。
考虑到系数调整的目的是尽可能地减小扰动的大小，这促使我们考虑如何减小扰动的大小。因此，我们不考虑成功率，而是根据实际降幅与预期降幅之比来调整系数α。实际降幅可直接计算，用两者距离之差为:

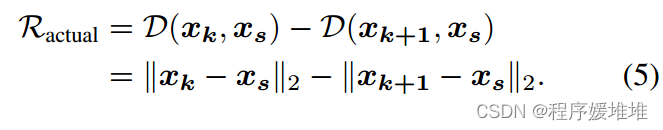
对于期望约简，我们将更新部分在源方向上的投影长度视为期望约简:

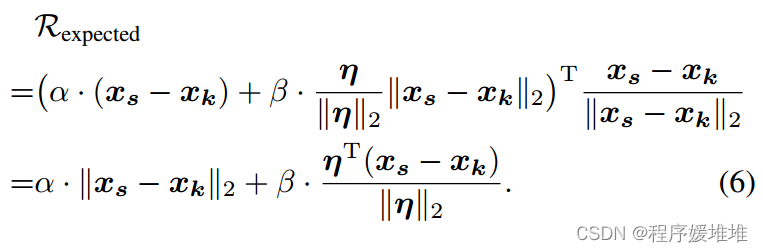
根据R_actual的值，有三种情况。当R_actual = 0时，我们知道发生了一个失败的查询，我们应该通过减少α来进行更多的探索。当R_actual > 0时，我们正在向源样本移动，现在0 < R_actual≤R_expected。因此R_actual/R_expected越大，表示源方向越重要，相应的系数α也就越大。当R_actual < 0时，优化方法很有可能陷入局部最优，应该远离源样本进行逃避。在这种情况下，R_actual≤R_expected < 0。对于属于[0,1]的值，我们计算的比率为R_expected/R_actual。同样，对于小比例，我们更倾向于选择小α，以帮助摆脱局部最优，而对于大比例，我们更倾向于选择大α，以防止优化方法不断远离源样本。综上所述，我们将R_actual与R_expected的比值统一为:

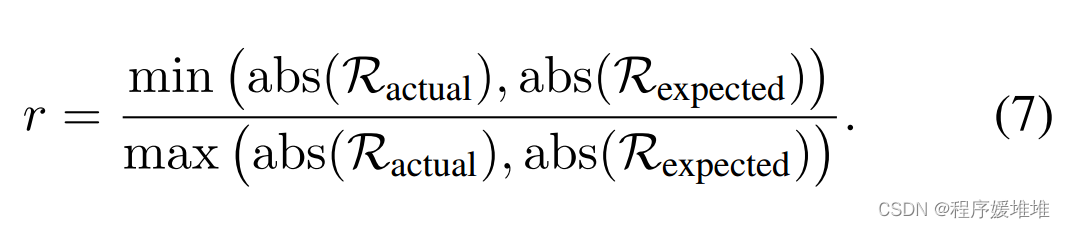
注意，比值r∈[0,1]，当r较大时增大系数α，反之减小系数α。对于失败的查询，x_k+1 = x_k, R_actual和比值r等于0。因此，我们可以发现，当r被映射为符号®时，基于成功率的方法只是我们方法的一个特殊情况。注意，太小的α可能导致永远的探索。因此，当α小于阈值时，我们重置α的值。最后，我们将系数α更新为:

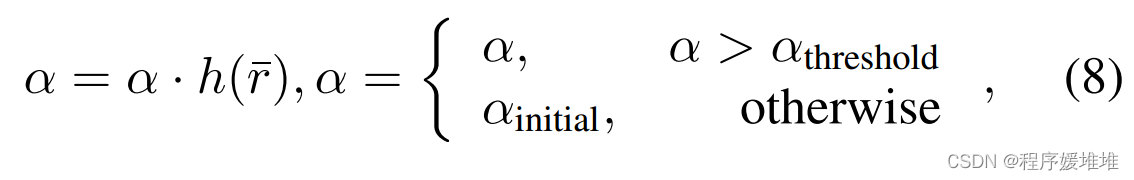
其中r¯是比值r在过去几次迭代中的平均值，h(·):[0,1]→R⁺是将比值映射到合适值的函数，α_threshold是防止α过小的值，α_initial是α的初始值。h(·)单调递增，取0 < h (0) < 1, h(1) > 1。本文实验选取h(·)为h(¯r) =(¯r + 0.8)²。

3.4 子空间抽样

大的解空间是黑盒攻击最主要的问题，人们提出了降维[21,10,23]和低频约束[3,24]等方法来减小解空间，这些方法确实加快了攻击过程。这些子空间优化方法与我们的方法是正交的，可以集成以进一步提高性能。考虑到双线性插值降维比其他方法更简单快捷，我们在低维空间对方向η进行采样，然后用双线性插值将其提升到原始输入空间。在[23]之后，低空间的维度将是原始空间的1/16。
我们将上述三部分相结合的方法称为自适应历史驱动攻击(AHA)，详细内容见alg1。