公钥加密模型

 

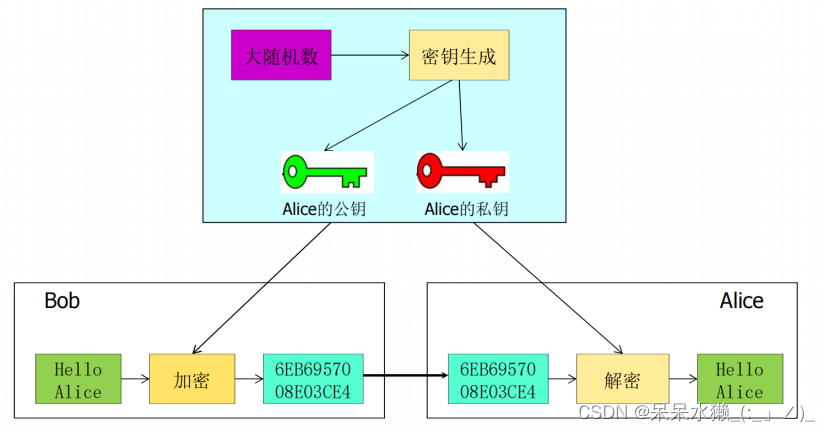
Ø 密钥生成过程：接收消息的端系统（如图中的接收者Alice）产生一对密钥(PKA ,SKA ), PKA 是公开钥（用于加密）， SKA 是秘密密钥（用于解密）.

Ø 加密过程：Bob想向Alice发送消息m，则获取Alice的公开密钥PKA ，加密得密文c = EPKA [m], 其中E是加密算法.

Ø 解密过程： Alice收到密文c后，用自己的秘密钥SKA 解密，表示为m = DSKA [c]，其中D是解密算法.

单向陷门函数

定义:一个定义在（X,Y）空间上的单向陷门函数(One-way Trapdoor functions, OTF )包含3个“有效”算法 (G, F, F -1)

n G(⋅): 随机算法，输出对(pk,sk)

n F(pk,⋅):确定算法，定义X->Y的运算

n F -1(sk,⋅): F(pk,⋅)的逆函数，定义Y->X的运算

对于任意生成的一对密钥G →(pk,sk),单向陷门函数满足：

x∈X: F-1(sk, F(pk, x) ) = x

定义: (G, F, F-1) 是一个安全的的OTF当对于所有有效的算法A:

AdvOW [A,F] = Pr[ A[F(pk, x)]=x] < 可忽略

RSA单向陷门函数及其应用

1） 密钥的产生

① 选两个安全的大素数p和q。

② 计算n=p×q，φ(n)=(p-1)(q-1),其中φ(n)是n的欧拉函数值。

③ 选一整数e，满足1<e<φ(n)，且gcd(φ(n),e)=1。

④ 计算d，满足d·e≡1 mod φ(n),即d是e在模φ(n)下的乘法逆元。因e与φ(n)互素，故它的乘法逆元存在且唯一。

⑤ {e,n}为公开密钥,{d,n}为秘密密钥。

2） 加密

加密时首先将明文分组，使得每个分组m值小于n，即分组长度小于log2 n。然后对每个明文分组m，作加密运算：c≡me mod n

3） 解密

对每个密文分组的解密运算：m≡cd mod n

4）正确性

证明： 若m与n互素，由加密过程知c≡me mod n，所以

cd mod n≡med mod n≡mkφ(n)+1 mod n

由Euler定理知mφ(n)≡1 mod n,

所以 mkφ(n)≡1 mod n,

进而 mkφ(n)+1≡m mod n，

即 cd mod n≡m.

 

6）安全性

整数分解问题：已知n是两个大素数的乘积，求n的素分解;

如果RSA加密算法的模数n被成功地分解为p×q，则获得φ(n)=(p-1)(q-1)，从而攻击者能够从公钥e解出私钥d，即d≡e -1 mod φ(n)，完全破译

 

RSA单向陷门函数及其应用

RSA的共模攻击：

若系统中用户共用一个模数n ，而拥有不同的e和d;

若存在同一明文（设为m）分别用不同的公钥（e1和e2）加密，

c1 = me1 mod n ；c2 = me2 mod n

设攻击者截获n、e1、e2、c1和c2， gcd(e1,e2)=1，则他可以恢复m 。

算法：因为e1和e2互质，故用Euclidean算法能找到r 和s，满足：

r * e1 + s * e2 = 1则

(c1)r * (c2)s = (me1 ) r * (me2 ) s mod n= m r * e1 + s * e2 mod n = m mod n