⭐️前言⭐️
本文主要总结一些常见的二叉树题目,希望读者能够通过这篇文章,来对二叉树有一个更深一步的了解。
🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁
🍉博主将持续更新学习记录收获,友友们有任何问题可以在评论区留言
🍉博客中涉及源码及博主日常练习代码均已上传GitHub

📍内容导读📍
- 🍅递归实现遍历
- 🍅非递归实现遍历
- 🍅层序遍历
- 🍅祖先节点
- 🍅序列化和反序列化
- 🍅求二叉树某个节点的后继节点
- 🍅折纸问题
- 🍅判断二叉树是不是完全二叉树
- 🍅总结
🍅递归实现遍历
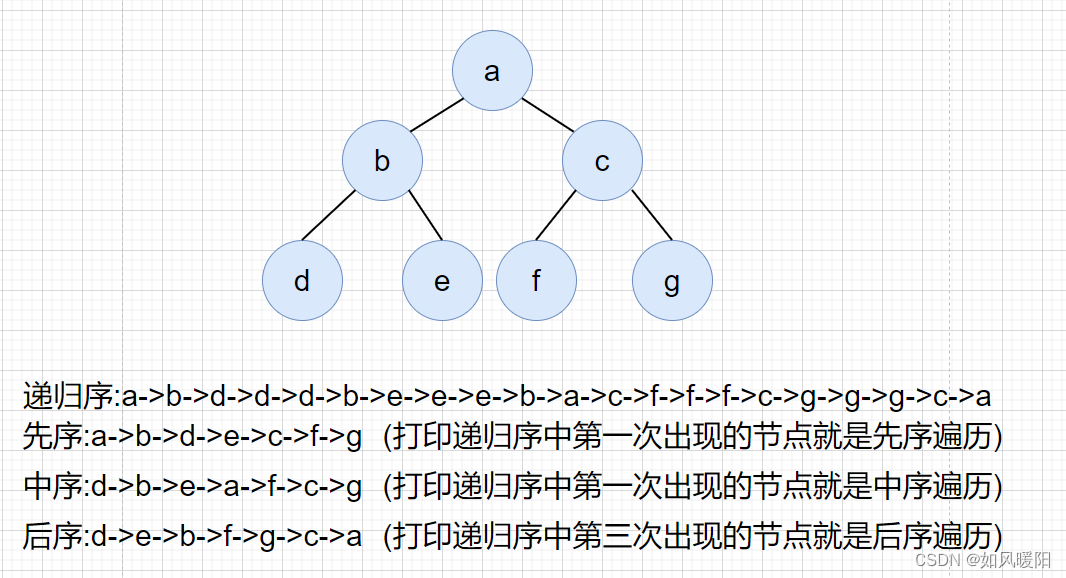
1)理解递归序(每个节点到达三次)
2)先序、中序和后序都可以在递归序的基础上加工出来
3)第一次到达一个节点就打印是先序、第二次打印即中序、第三次即后序
144. 二叉树的前序遍历
class Solution {
List<Integer> res=new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
if(root==null) {
return new ArrayList<>();
}
res.add(root.val);
preorderTraversal(root.left);
preorderTraversal(root.right);
return res;
}
}
145. 二叉树的后序遍历
class Solution {
List<Integer> res=new ArrayList<>();
public List<Integer> postorderTraversal(TreeNode root) {
if(root==null) {
return new ArrayList<>();
}
postorderTraversal(root.left);
postorderTraversal(root.right);
res.add(root.val);
return res;
}
}
94. 二叉树的中序遍历
class Solution {
List<Integer> res=new ArrayList<>();
public List<Integer> inorderTraversal(TreeNode root) {
if(root==null) {
return new ArrayList<>();
}
inorderTraversal(root.left);
res.add(root.val);
inorderTraversal(root.right);
return res;
}
}
🍅非递归实现遍历
借助栈,来通过系统栈改为stack栈,将递归改为非递归。
前序:
先入栈的后出栈,所以先入右子树,再入左子树,那么弹出顺序就是先左子树,再右子树,就符合前序根左右的顺序。
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res=new ArrayList<>();
if(root==null) {
return res;
}
Stack<TreeNode> stack=new Stack<>();
stack.push(root);
while(!stack.isEmpty()) {
TreeNode cur=stack.pop();
res.add(cur.val);
if(cur.right!=null) stack.push(cur.right);
if(cur.left!=null) stack.push(cur.left);
}
return res;
}
}
中序:
递归左子树到最底层,再依次往上回溯记录。
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res=new ArrayList<>();
if(root==null) return res;
Stack<TreeNode> stack=new Stack<>();
TreeNode cur=root;
while(cur!=null||!stack.isEmpty()) {
if(cur!=null) {
stack.push(cur);
cur=cur.left;
}else {
cur=stack.pop();
res.add(cur.val);
cur=cur.right;
}
}
return res;
}
}
后序:
前序遍历的调整,加入根节点后,先入左子树,再入右子树,那么弹出顺序就是根右左,将结果逆序即为后序遍历结果。
class Solution {
List<Integer> res=new ArrayList<>();
public List<Integer> postorderTraversal(TreeNode root) {
if(root==null) return new ArrayList<>();
Stack<TreeNode> stack=new Stack<>();
stack.push(root);
while(!stack.isEmpty()) {
TreeNode cur=stack.pop();
res.add(cur.val);
if(cur.left!=null) stack.push(cur.left);
if(cur.right!=null) stack.push(cur.right);
}
Collections.reverse(res);
return res;
}
}
🍅层序遍历
https://leetcode.cn/problems/binary-tree-level-order-traversal/description/
二叉树的按层遍历借助队列来实现
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res=new ArrayList<>();
if(root==null) return res;
Queue<TreeNode> queue=new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
int size=queue.size();
List<Integer> row=new ArrayList<>();
while(size-->0) {
TreeNode cur=queue.poll();
row.add(cur.val);
if(cur.left!=null) queue.offer(cur.left);
if(cur.right!=null) queue.offer(cur.right);
}
res.add(row);
}
return res;
}
}
429. N 叉树的层序遍历
class Solution {
public List<List<Integer>> levelOrder(Node root) {
List<List<Integer>> res=new ArrayList<>();
if(root==null) return res;
Queue<Node> queue=new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
int size=queue.size();
List<Integer> row=new ArrayList<>();
while(size-->0) {
Node cur=queue.poll();
row.add(cur.val);
List<Node> children=cur.children;
for(Node child:children) {
if(child!=null) queue.offer(child);
}
}
res.add(row);
}
return res;
}
}
🍅祖先节点
二叉树节点x的所有祖先节点
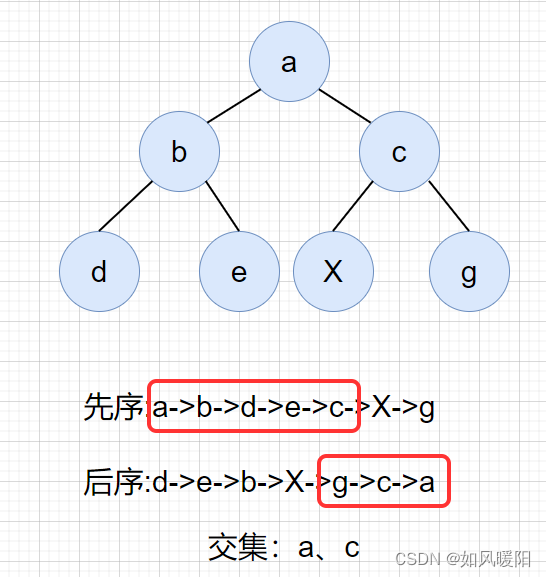
证明:
1、证明祖先节点前序X左,后序X右:
因为先序遍历是先遍历根节点,再去遍历左右子树,所以所有的祖先节点一定出现在节点X以左;同理,后序遍历最后遍历的根节点,所以所有的祖先节点一定出现在X以右。
2、证明交集即为祖先节点:
针对节点X,二叉树上的所有节点可以分为四类,祖先节点、左兄节点、右兄节点和孩子节点。
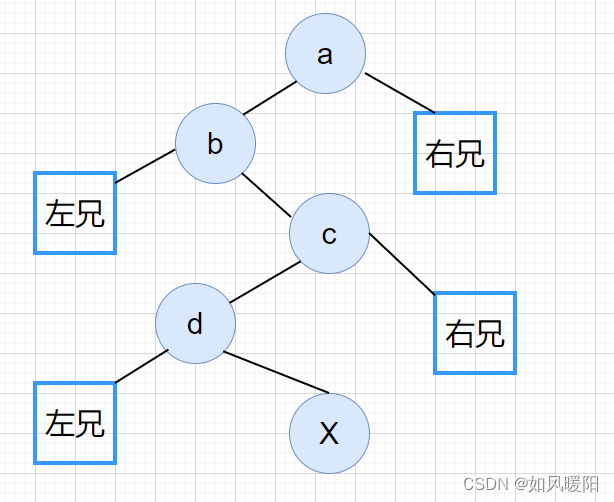
在先序遍历中,X节点的左边部分不可能包含孩子节点和右兄节点;
在后序遍历中,X节点的右边部分不可能包含左兄节点;
所以两者的交集即为仅祖先节点。
🍅序列化和反序列化
297. 二叉树的序列化与反序列化
序列化不过就是把结构化的数据打平,本质是在考察二叉树的遍历方式。
public class Codec {
String SEP=",";
String NULL="#";
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
StringBuffer sb=new StringBuffer();
serialize(root,sb);
return sb.toString();
}
void serialize(TreeNode root,StringBuffer sb) {
if(root==null) {
sb.append(NULL).append(SEP);
return;
}
sb.append(root.val).append(SEP);
serialize(root.left,sb);
serialize(root.right,sb);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
LinkedList<String> nodes=new LinkedList<>();
for(String s:data.split(SEP)) {
nodes.addLast(s);
}
return deserialize(nodes);
}
TreeNode deserialize(LinkedList<String> nodes) {
if(nodes.isEmpty()) return null;
String first=nodes.removeFirst();
if(first.equals(NULL)) return null;
TreeNode root=new TreeNode(Integer.parseInt(first));
root.left=deserialize(nodes);
root.right=deserialize(nodes);
return root;
}
}
🍅求二叉树某个节点的后继节点
题目:
二叉树结构如下定义:
Class Node {
V value;
Node left;
Node right;
Node parent;
}
给你二叉树中的某个节点,返回该节点的后继节点
题解思路:
后继节点的定义为:中序遍历结果中,该节点紧挨的后一个节点即为其后继节点。
因为节点的定义中有parent指针,所以可以通过先得到中序遍历结果,再去寻找某节点的后继节点,但是这种方式时间复杂度太高。
可以根据中序遍历的特性,直接去找到其后继节点。
如果该节点有右子树,那么其右子树的最左节点即为其后继节点;否则,其后继节点,是该节点为左树的最左节点的根节点。
代码实现:
public class NextNode {
public static class Node {
public int value;
public Node left;
public Node right;
public Node parent;
public Node(int value) {
this.value = value;
}
}
public static Node getNextNode(Node node) {
if(node==null) {
return node;
}
if(node.right!=null) return getLeftMost(node.right);
else { // 无右子树
Node parent=node.parent;
while (parent!=null&&parent.right==node) { // 当前节点是其父亲节点的右孩子
node=parent;
parent=node.parent;
}
// 如果因为parent为null而跳出,说明没有后继节点,该节点即为最右节点。
return parent;
}
}
public static Node getLeftMost(Node node) {
if(node==null) {
return node;
}
while (node.left!=null) {
node=node.left;
}
return node;
}
}
🍅折纸问题
题目:
请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开
此时折痕是凹下去的,即折痕突起的方向指向纸条的背面
如果从纸条的下边向上方连续对折2次,压出折痕后展开
此时有三条折痕,从上到下依次是下折痕、下折痕和上折痕。
给定一个输入参数N,代表纸条都从下边向上方连续对折N次
请从上到下打印所有折痕的方向。
N=1时,打印: down
N=2时,打印: down down up
题解思路:
该题目可以先通过折纸来去发现规律,其实折痕的信息就是一棵二叉树的中序遍历结果,该二叉树的特点如下:
1、根节点为down
2、所有左子树的根节点为down
3、所有右子树的根节点为up
遍历该二叉树,并记录其中序遍历结果即为所求。
纸条对折三次,折痕信息如下所示
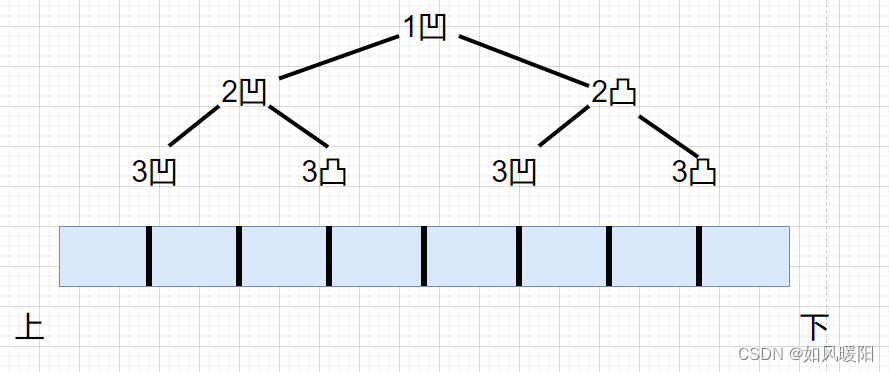
代码实现:
public class PaperFolding {
public static void printAllFolds(int N) {
process(1,N,true);
}
public static void process(int i,int N,boolean fold) {
if(i>N) {
return;
}
process(i+1,N,true);
System.out.print(fold?"down ":"up ");
process(i+1,N,false);
}
public static void main(String[] args) {
int N=3;
printAllFolds(N);
}
}
🍅判断二叉树是不是完全二叉树
题解思路:
与相同深度的满二叉树的节点编号一一对应的二叉树就是完全二叉树。
判断是否是完全二叉树可以通过以下两个条件来判断:
1、任意节点如果有右子树而没左子树,则不是完全二叉树。
2、如果遇到左右节点不全的节点,则层序遍历的后序节点必须是叶子节点,否则则不是完全二叉树。
代码实现:
public class IsCBT {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int value) {
this.value = value;
}
}
public static boolean isCBT(Node head) {
if(head==null) {
return true; // 如果为空树默认是完全二叉树
}
Queue<Node> queue=new LinkedList<>();
// 是否遇到过左右孩子不全的节点
boolean leaf=false;
Node left=null;
Node right=null;
queue.offer(head);
while (!queue.isEmpty()) {
head=queue.poll();
left=head.left;
right=head.right;
if((leaf&&(left!=null||right!=null))||(left==null&&right!=null)) return false;
if(left!=null) queue.offer(left);
if(right!=null) queue.offer(right);
if(left==null||right==null) leaf=true;
}
return true;
}
}
🍅总结
遇到二叉树的题目的通用思考过程是:是否可以通过遍历一遍二叉树得到答案?如果不能的话,是否可以定义一个递归函数,通过子问题的答案推导出原问题的答案?如果题目需要子树信息,使用后序遍历(即在后序位置上搞事情)
⭐️最后的话⭐️
总结不易,希望uu们不要吝啬你们的👍哟(^U^)ノ~YO!!如有问题,欢迎评论区批评指正😁







![[Golang] 爬虫实战-获取动态页面数据-获取校招信息](https://img-blog.csdnimg.cn/ed1783558dfa434ab6e44ae52069de24.png)