Embedding Entire Graphs

一、图嵌入向量基本概念

与Node Embeddings不同，Graph Embeddings是对整个图或子图进行编码而忽略其中的节点。应用场景包括异常检测或分子有毒检测。

二、对Node Embeddings求和或求和后平均

如图，首先对图/子图中的节点进行图嵌入向量表示（$z_u$），之后将嵌入向量求和（或对求和向量再平均）得到图/子图的嵌入向量。

注意：该方法虽然很简单，但是效果很好。

三、创建超节点

如图，在原图的基础上对图/子图增加一个超节点，该超节点与图/子图的所有节点均建立连接。之后利用Node Embeddings的方法求得该节点的嵌入向量，该嵌入向量就是图/子图的嵌入向量。

四、匿名随机游走

1、匿名随机游走方法：

匿名随机游走，只记忆节点出现的时间而不关心具体的节点。

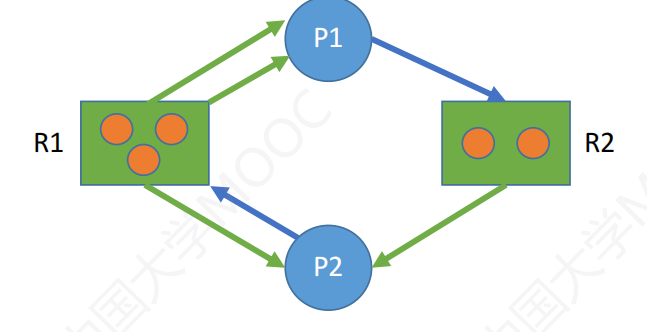
如图，在A、B、C、D、E和F节点组成的子图中：

第一次游走的节点次序为：A、B、C、B、C。A是第一个访问的节点标记为1，B是第二个访问的节点标记为2，C是第三个访问的节点标记为3，除此之外没有其他节点。此时，匿名随机游走路径为：1、2、3、2、3；

第二次游走的节点次序为：C、D、B、D、B。C是第一个访问的节点标记为1，D是第二个访问的节点标记为2，B是第三个访问的节点标记为3，除此之外没有其他节点。此时，匿名随机游走路径为：1、2、3、2、3；

从两次行走中可以看出，虽然两次行走的路径不同，但是其匿名行走路径是相同的。只记忆节点出现的时间而不关心具体的节点。

从图中可以看出，对于不同长度的匿名随机游走序列，其行走路径数量呈指数级爆炸增长。

其中，长度为3的路径次数计算如图：

2、使用匿名随机游走进行图嵌入编码

对于图/子图，进行固定长度的匿名随机游走，并记录每个行走序列的次数（或出现概率），将其记录为向量，该向量即为图的嵌入向量。如图：

随机游走的长度$l$是一个超参数，对于选定的$l$，应该对图/子图采样多少次是一个值得思考的问题，如图：

为了保证采样的健壮性，使采样的分布误差保持在$[\epsilon ,\delta ]$之间，对于选定长度$l$，计算得到随机游走序列的个数为$\eta $（查表或自己计算），得到采样次数$m$为：
$$m=\lceil \frac{2}{{\epsilon }^2}\left(log\left(2^{\eta }-2\right)-log(\delta )\right)\rceil$$
例如：对于长度$l$的随意游走序列，游走序列$\eta$有877种，定义分布误差为$[\epsilon =0.1,\delta =0.01]$，计算得到$m$为122500次。

五、Learn Walk Embeddings

该方法与匿名随机游走的区别是：匿名随机游走只产生一个嵌入向量来计算不同游走序列的次数（概率）而本方法对每种匿名游走序列单独嵌入编码，同时加上一个图/子图的嵌入向量。

其中，图/子图的嵌入向量为$z_G$，匿名随机游走序列嵌入向量 Z = { z i : 1... η } Z=\{z_i:1...\eta\} Z={zi​:1...η}。$\eta$为固定游走长度后的游走序列总个数。

具体步骤为：

1. 建立一个上下文管理器，$N_R(u)$记录以$u$为游走起点的游走路径，总数为$T$个。
2. 上下文自监督：对于前$\Delta$次已经出现的游走序列，预测第$\Delta +1$次出现的序列（类似于NLP中transformer-decoder的算法）。优化函数如上图。

上下文自监督的具体步骤为：

首先将前$\Delta$次出现的游走序列向量 { z t − Δ , . . . z t − 1 } \{ \mathbb{z}_{t-\Delta},...\mathbb{z}_{t-1} \} {zt−Δ​,...zt−1​}求和并取平均，再与全图嵌入向量$z_G$堆叠。之后通过线性变化和softmax计算第$\Delta +1$次出现的游走序列。重复以上过程反复更新所有$z$向量。注意采用负样本来优化计算。

六、总结

图片截选自——斯坦福CS224W: Machine Learning with Graphs