7.1 算法解释

动态规划 解决有很多重叠子问题 的情况的最优解时有效，它将问题重新组合成子问题。为了防止多次解决子问题，它们的结果都逐渐被计算并保存，从简单的问题直到整个问题都被解决。因此，动态规划保存递归时的结果，不会在解决同样问题的时候浪费时间。

动态规划只能应用于有最优子结构的问题，最优子结构指的是局部最优解能决定全局最优解（对有些问题这个要求并不能完全满足，因此有时需要引入一定的近似）。

解决动态规划问题的关键是找到状态转移方程，可以通过计算和存储子问题的解来求解最终问题。

同时，也可以对动态规划进行空间压缩，起到节省空间消耗的效果。

在一些情况下，动态规划可以看作是带有状态记录的优先搜索，如果一个子问题在优先搜索时已经计算过一次，可以把它的结果存储下来，之后遍历到该子问题的时候可以直接返回存储的结果。动态规划是自下而上的，即先解决子问题，再解决父问题；而带有状态记录的优先搜索是自上而下的，即从父问题搜索到子问题，若重复搜索到同一个子问题则进行状态记录，防止重复计算。如果题目需求的是最终状态，那么使用动态搜索比较方便；如果题目需要输出所有的路径，那么使用带有状态记录的优先搜索比较方便。

7.2 基本动态规划：一维

70. 爬楼梯（简单）

思路及代码： 70. 爬楼梯

198.打家劫舍（中等）

思路及代码： 198.打家劫舍

413. 等差数列划分（中等）

思路及代码： 413. 等差数列划分

7.3 基本动态规划：二维

64. 最小路径和（中等）

思路及代码： 64. 最小路径和

542. 01 矩阵（中等）

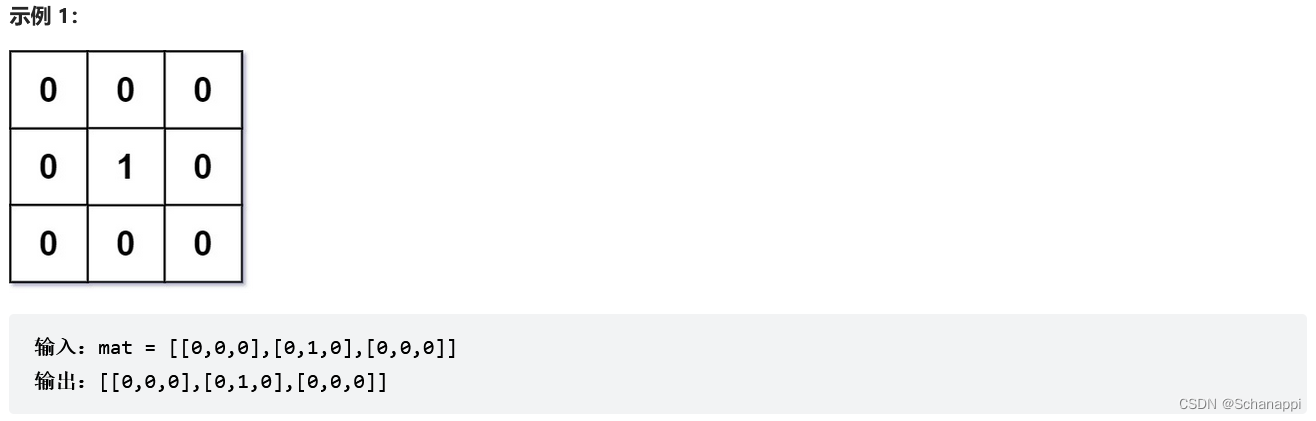
思路及代码： 542. 01 矩阵

221.最大正方形（中等）

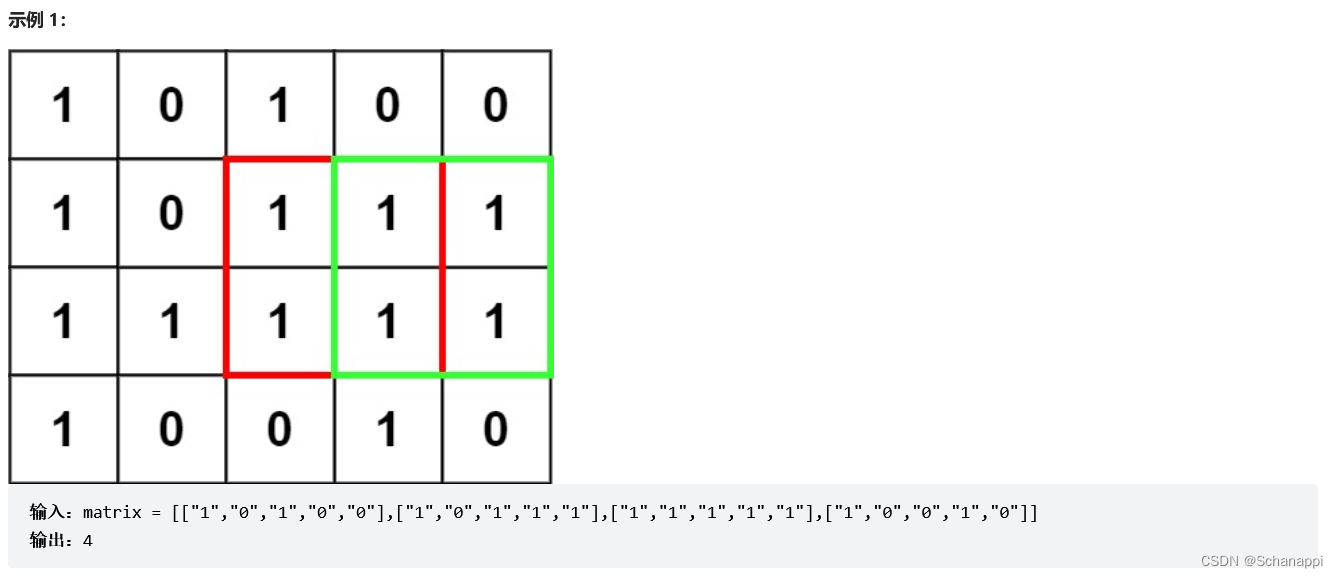
思路及代码： 221.最大正方形

7.4 分割类型题

279. 完全平方数（中等）

思路及代码： 279. 完全平方数

91. 解码方法（中等）

思路及代码： 91. 解码方法

139. 单词拆分（中等）

思路及代码： 139. 单词拆分

7.5 子序列问题

300. 最长递增子序列（中等）

思路及代码： 300. 最长递增子序列

1143. 最长公共子序列（中等）

思路及代码： 1143. 最长公共子序列

7.6 背包问题

背包问题是一种组合优化的 NP 完全问题：有 N 个物品和容量为 W 的背包，每个物品都有自己的体积 w 和价值 v ，求拿哪些物品可以使背包所装下物品的总价值最大。

如果限定每种物品只能选择 0 个或 1 个，则此问题称为 0-1背包问题；如果不限定每种物品的数量，则称为无边界背包问题或完全背包问题。

1. 使用动态规划解决背包问题，以 0-1 背包问题为例，定义二维数组 dp存储最大价值，其中 dp[i][j] 表示前 i 件物品体积不超过 j 的情况下能达到的最大价值。在遍历到第 i 件物品时，在当前背包总容量为 j 的情况下，如果我们不将物品 i 放入背包，那么 dp[i][j] = d[i-1][j] ，即前 i 个物品的最大价值等于只取前 i-1 个物品时的最大价值；如果将物品 i 放入，假设第 i 件物品体积为 w ，价值为 v ，那么得到 dp[i][j] = dp[i-1][j-w] + v 。我们只需要在遍历过程中对两种情况取最大值即可，总时间复杂度和空间复杂度都为 O（NW）。

       int knapsack(vector<int> weights, vector<int> values, int N, int W){
           vector<vector<int>> dp(N+1, vector<int>(W+1, 0));
           for(int i=1; i<=N; ++i){
               int w = weights[i-1], v = values[i-1];
               for(int j=1; j<=W; ++j){
                   if(j >= w){
                       // 当前背包容量>=w
                       dp[i][j] = max(dp[i-1][j], dp[i-1][j-w] + v);
                   }
                   else{
                       dp[i][j] = dp[i-1][j];
                   }
               }
           }
           return dp[N][W];
       }
   

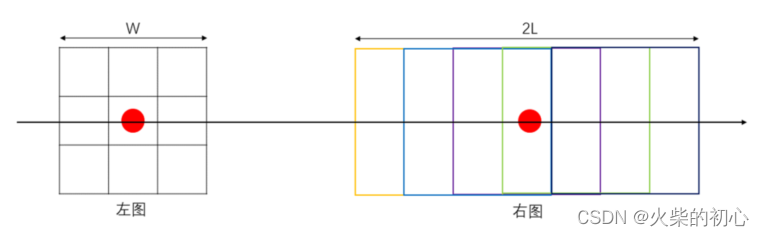
2. 可以进一步对 0-1背包进行空间优化， 将空间复杂度降为 O（W）。如图，假设目前考虑物品 i = 2， 它的体积 w = 2， 价值 v = 3；对于背包容量 j，我们可以得到 dp[2][j] = max(dp[1][j], dp[1][j-2] + 3) 。不难发现，永远只依赖于上一排 i = 1 的信息，之前算过的其他物品都不需要再使用。因此我们可以去掉 dp 矩阵的第一个维度，在考虑物品 i 时，变成 dp[j] = max(dp[j], dp[j-w] + v) 。需要注意，在遍历每一行的时候都需要逆向遍历 ，这样才能调用上一行物品 i-1 时 dp[j-w] 的值 ；如果按照从左到右的正序遍历，则 dp[j-w] 的值在遍历到 j 之前就已经被更新成物品 i 的值了。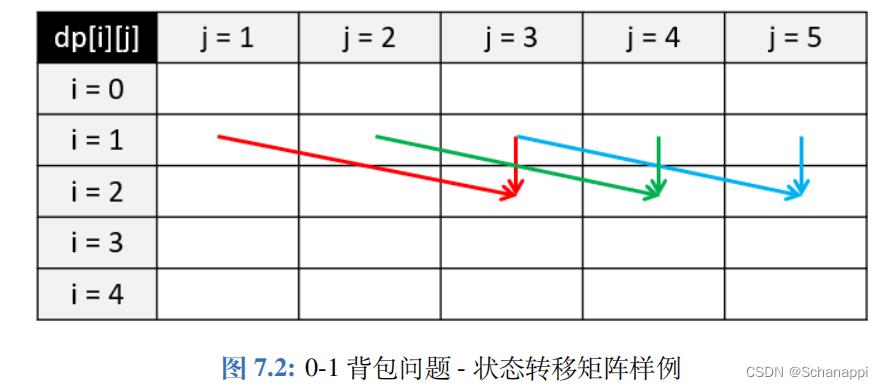

   

       int knapsack(vector<int> weights, vector<int> values, int N, int W){
           vector<int> dp(W+1, 0);
           for(int i=1; i<=N; ++i){
               int w = weights[i-1], v = values[i-1];
               for(int j=W; j>=w; --j){
                   dp[j] = max(dp[j], dp[j-w] + v);
               }
           }
           return dp[W];
       }
   

3. 在完全背包问题中，一个物品可以拿多次。如图所示，假设我们遍历到物品 i=2 时，且其体积为 w=2， 价值为 v=3；对于背包容量 j=5，最多只能装下两个该物品。那么状态转移方程就变成 dp[2][5] = max(dp[1][5], dp[1][3] + 3, dp[1][1] + 6) ，如果采用这种方法，假设背包容量无穷大，而物品大小无穷小，那么比较次数也会趋近于无穷大，远远超过 O（NW） 的比较次数。

   

   怎么解决这个问题呢？不难发现，在 dp[2][3] 的时候，我们其实已经考虑了 dp[1][3] 和 dp[2][1] 的情况，而 dp[2][1] 也已经考虑了 dp[1][1] 的情况。因此，如下图所示，对于拿多个物品的情况，只需要考虑 dp[2][3] 即可，即 dp[2][5] = max(dp[1][5], dp[2][3] +3) 。这样，我们就得到了完全背包问题的状态转移方程：dp[i][j] = max(dp[i-1][j], dp[i][j-w] + v) ，和 0-1背包问题不同的是，第二个 i-1 替换成 i 。

   

       int knapsack(vector<int> weights, vector<int> values, int N, int W){
           vector<vector<int>> dp(N+1, vector<int>(W+1, 0));
           for(int i=1; i<=N; ++i){
               int w = weights[i-1], v = values[i-1];
               for(int j=1; j<=W; +j){
                   if(j>=w)    dp[i][j] = max(dp[i-1][j], dp[i][j-w] + v);
                   else dp[i][j] = dp[i-1][j];
               }
           }
           return dp[N][W];
       }
   

   同样地，可以利用 空间压缩将时间复杂度降低为 O（W）。需要注意，遍历的时候需要 正向遍历 ，因为我们需要利用当前物品在 第 j-w 列的信息。

       int knapsack(vector<int> weights, vector<int> values, int N, int W){
           vector<int> dp(W+1, 0);
           for(int i=1; i<=N; ++i){
               int w = weights[i-1], v = values[i-1];
               for(int j=w; j<=W; +j){
                   if(j>=w)    dp[j] = max(dp[j], dp[j-w] + v);
                   else dp[j] = dp[j];
               }
           }
           return dp[W];
       }
   

4. 在思考空间压缩前，先画出状态转移方程，方便思考如何进行空间压缩。此外，有一个简单的口诀：「0-1背包对物品的迭代放在外面，里面的体积或价值逆向遍历；完全背包对物品的迭代放在里层，外层的体积或价值正向遍历」。

416. 分割等和子集（中等）

思路及代码： 分割等和子集

474. 一和零（中等）

思路及代码： 一和零

322. 零钱兑换（中等）

思路及代码：零钱兑换

7.7 字符串编辑

72. 编辑距离（困难）

思路及代码： 编辑距离

650. 只有两个键的键盘（中等）

思路及代码： 只有两个键的键盘

10. 正则表达式匹配（困难）

思路及代码： 正则表达式匹配

7.8 股票交易

股票交易类问题通常使用动态规划解决，对于稍微复杂的股票交易类问题，比如需要冷却时间或交易费用，则可以通过动态规划实现的状态机解决。

121. 买卖股票的最佳时机（简单）

思路及代码：买卖股票的最佳时机

188. 买卖股票的最佳时机 IV（困难）

思路及代码：188. 买卖股票的最佳时机 IV

309.最佳买卖股票时机含冷冻期（中等）

思路及代码： 309.最佳买卖股票时机含冷冻期

7.9 练习

213. 打家劫舍 II（中等）

思路及代码： 213. 打家劫舍 II

53. 最大子数组和（中等）

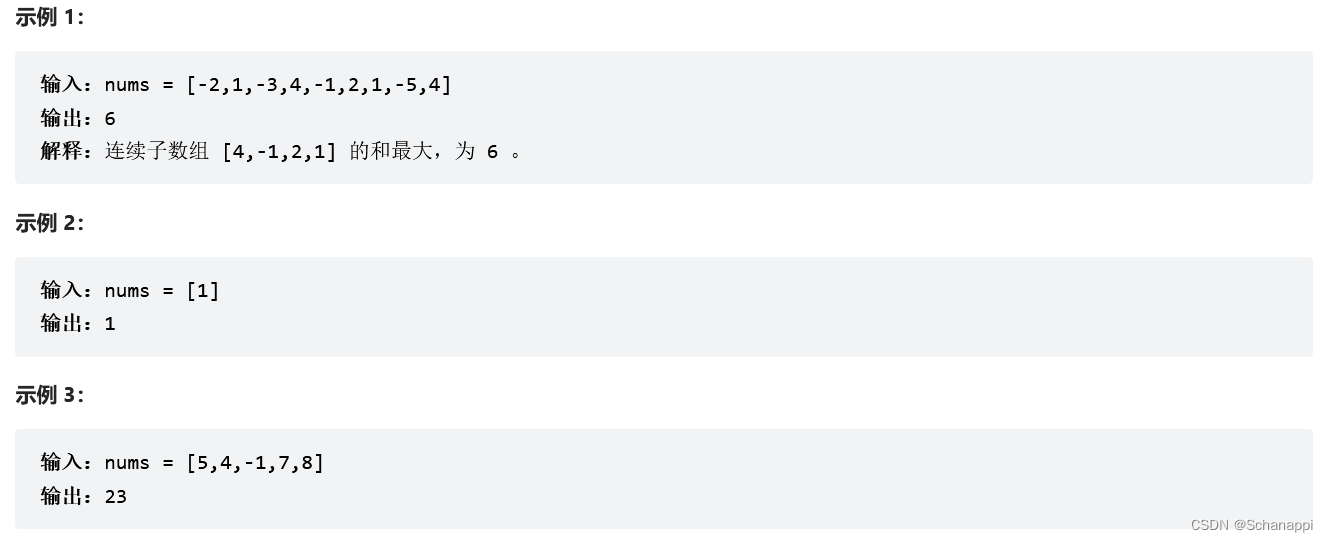
思路及代码：53. 最大子数组和

343. 整数拆分（中等）

思路及代码： 343. 整数拆分

583. 两个字符串的删除操作（中等）

思路及代码： 583. 两个字符串的删除操作

646. 最长数对链（中等）

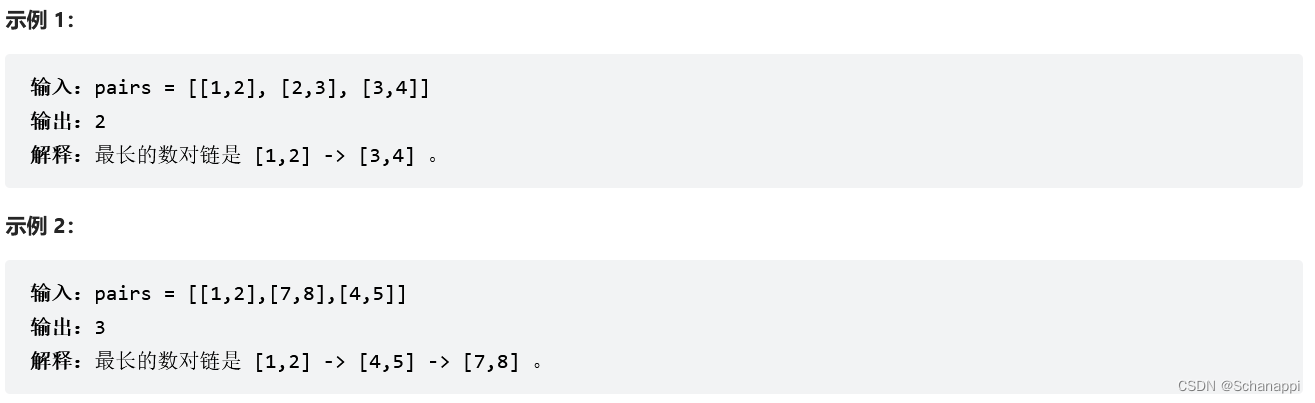
思路及代码： 646. 最长数对链

376. 摆动序列（中等）

思路及代码： 376.摆动序列

494. 目标和（中等）

思路及代码： 494. 目标和

714. 买卖股票的最佳时机含手续费（中等）

思路及代码： 714. 买卖股票的最佳时机含手续费

总结

1. 其实做下来，发现动态规划的思考过程都是一样的，分为四个步骤：

   • 状态定义；
   • 确定状态转移方程；
   • 初始化的考虑；
   • 确定最终的返回结果。

2. 题目分类：

   • 「基本动态规划：一维、二维」：都比较简单，当前状态一般只需要考虑上一个状态，基本上很容易进行空间压缩；

   • 「分割类型题」：需要确定分隔位置，因此状态转移方程比较复杂，有时候需要考虑每一种情况；

   • 「子序列问题」：子序列不要求连续，但如果是子数组或子字符串必须连续。对于子序列问题，有两种动态规划方法：

     • 第一种动态规划方法：定义 dp 数组，其中 dp[i] 表示以 i 结尾的子序列的性质。在处理好每个位置后，统计一遍各个位置的结果即可得到题目要求的结果。
     • 第二种动态规划方法：「定义一个 dp 数组，其中 dp[i]表示到位置 i 为止的子序列性质，并不是必须以 i 结尾」，此时 dp 数组的最后一位即为题目所求，不需要对每个位置进行统计。

   • 「背包问题」：背包问题又分为 0-1 背包问题 和 完全背包问题，一般定义二维数组 dp 存储最大价值，其中 dp[i][j] 表示前 i 件物品体积不超过 j 的情况下能达到的最大价值 。

     对于背包问题，空间压缩比较复杂。在思考空间压缩前，先画出状态转移方程，方便思考如何进行空间压缩。此外，有一个简单的口诀：「0-1背包对物品的迭代放在外面，里面的体积或价值逆向遍历；完全背包对物品的迭代放在里层，外层的体积或价值正向遍历」。

   • 「字符串编辑问题」：这类问题一般会对两个字符进行比较，因此定义 dp[i][j] 表示第一个字符串到 i ，第二个字符串到 j 的性质。然后思考 str[i] 和 str[j] 之间的关系，可能需要对每种情况进行分析。

   • 「股票交易问题」：这类问题如果建立状态机就很容易得出答案。一般分为 持有 和 不持有 股票两种情况进行讨论，定义 buy 和 sell 两个一维数组，分别表示买入（持有）和卖出（不持有）股票时候的最大收益。由于状态一般只和前一天的状态有关系，所以也很容易就进行空间压缩。对于初始化需要仔细考虑。