LeetCode---回溯算法中的子集问题

news2024/11/17 21:45:11

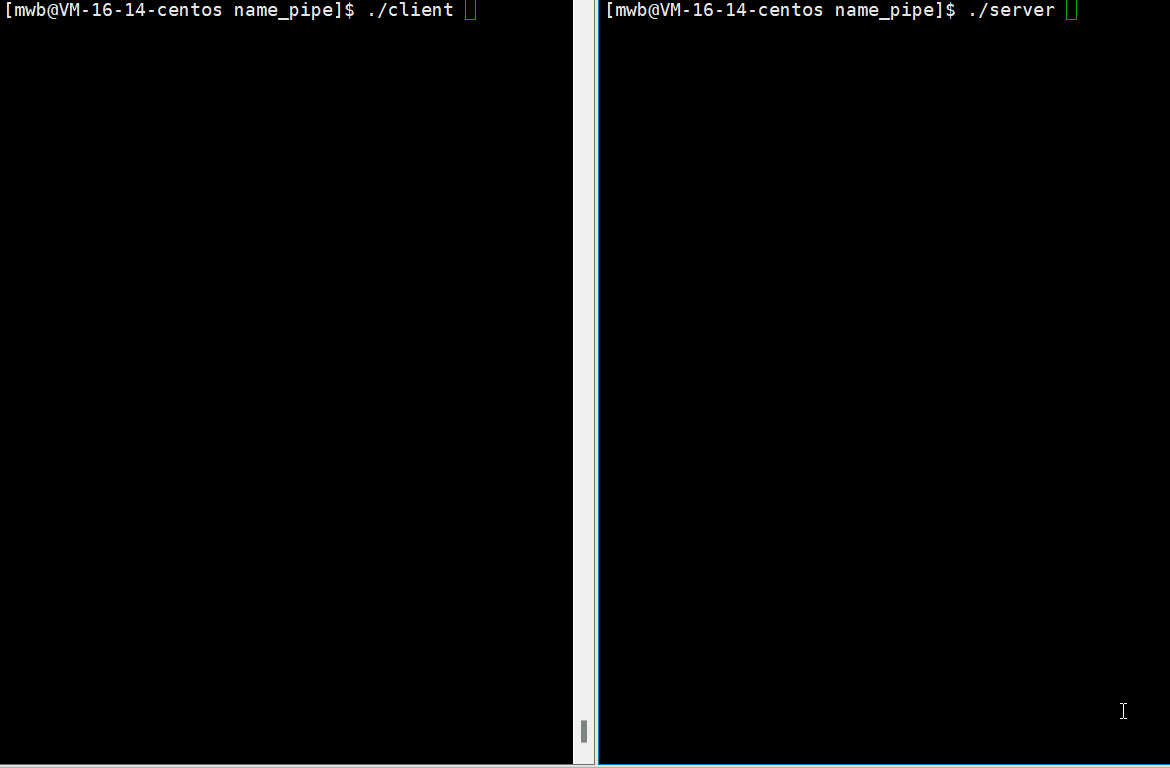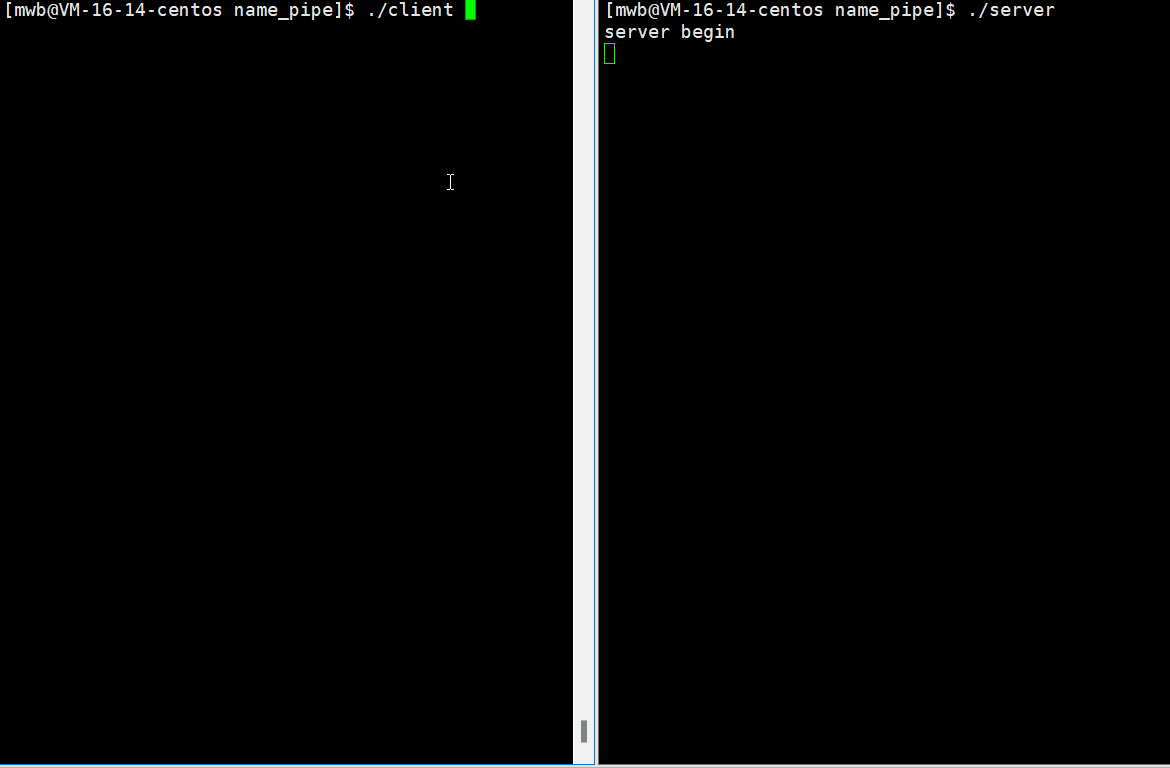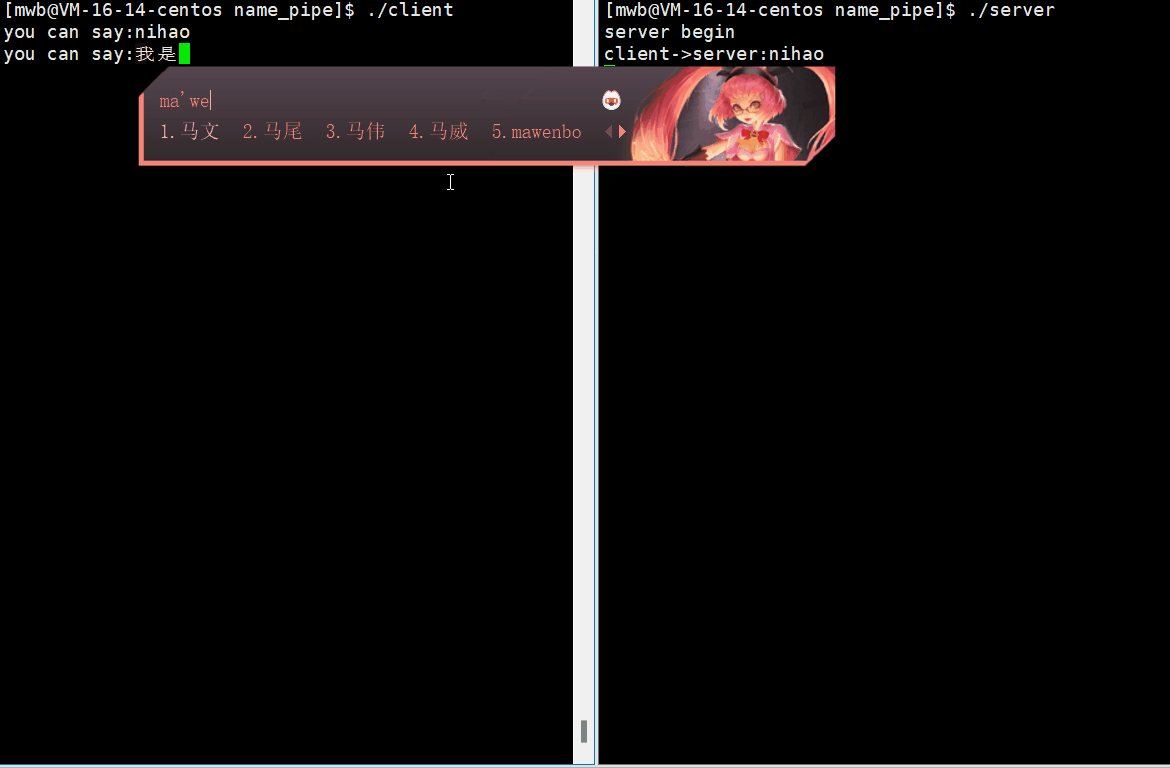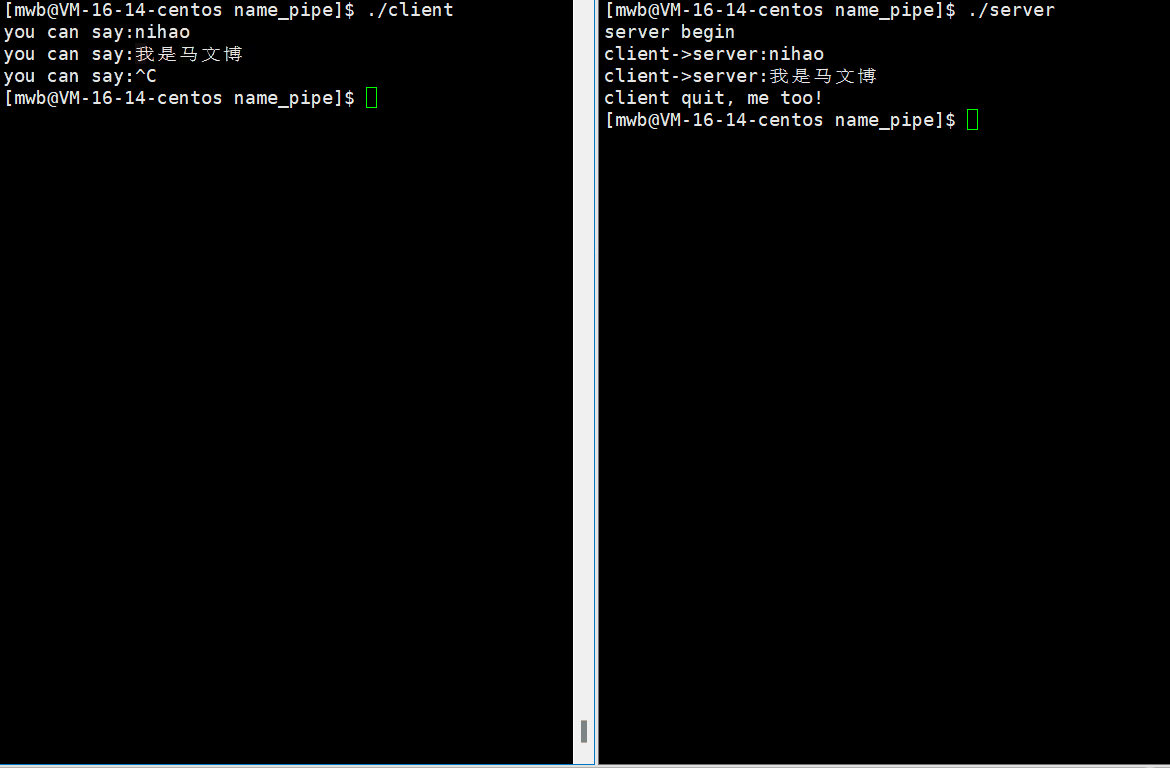
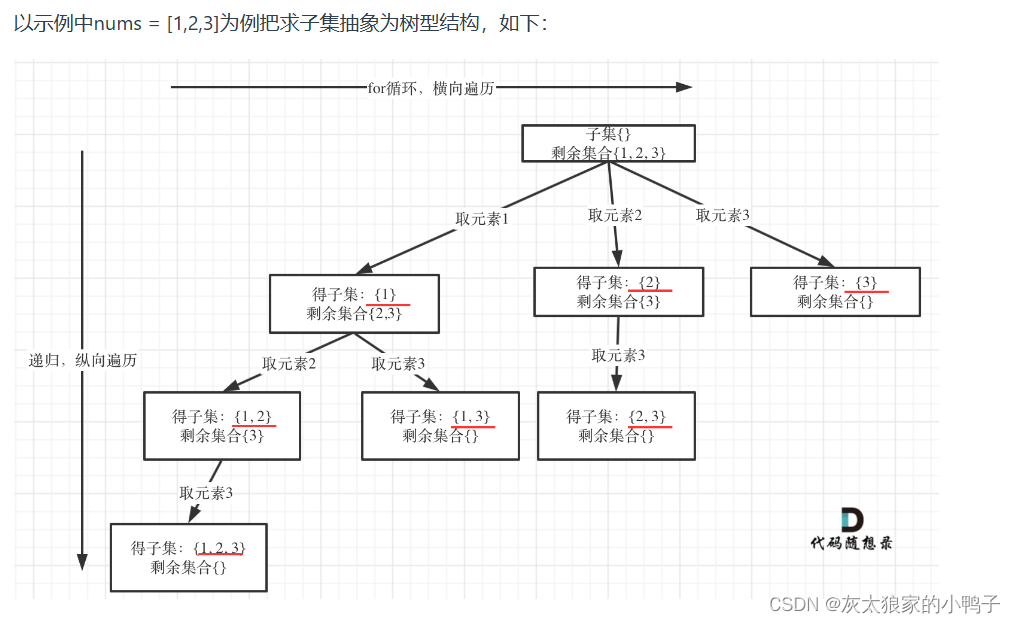
78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

回溯算法模板：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }
 
    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

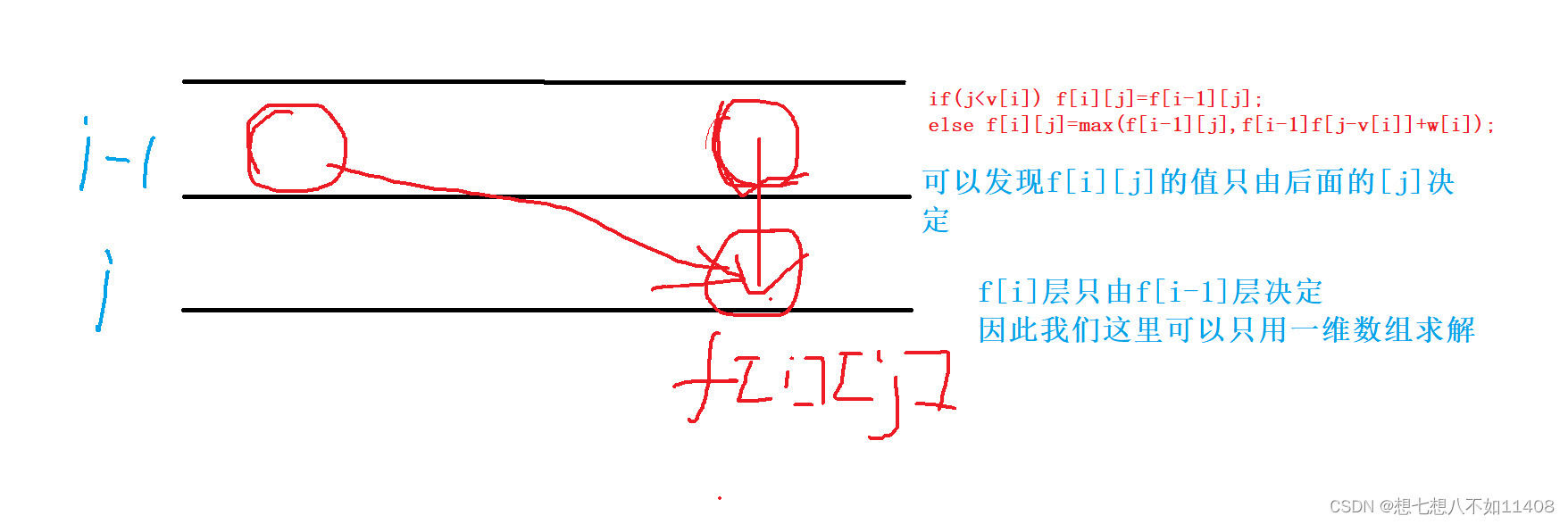
本题解析：因为子集（1，2）和子集（2，1)是一样的子集，所以需要startIndex来区分；在排列问题中startIndex是从0开始。子集问题是取树的每个节点，而在分割问题和组合问题中，是取数的叶子节点。

List<List<Integer>> res=new ArrayList<>();
    List<Integer> set=new ArrayList<>();
    public List<List<Integer>> subsets(int[] nums){
        backTracking(nums,0);
        return res;
    }

    /**
     * 子集问题是要求取到树的每个节点：
     * @param nums
     * @param startIndex
     */
    public void  backTracking(int[] nums,int startIndex){
        //子集问题是将树的每个节点都加入到set中；
        res.add(new ArrayList<>(set));
        //回溯终止条件：
        if (startIndex>=nums.length){
            return;
        }

        //单层回溯：
        for (int i= startIndex ;i<nums.length;i++){
            set.add(nums[i]);
            //递归
            backTracking(nums,i+1);
            //回溯：
            set.remove(set.size()-1);
        }
        
    }

90. 子集 II

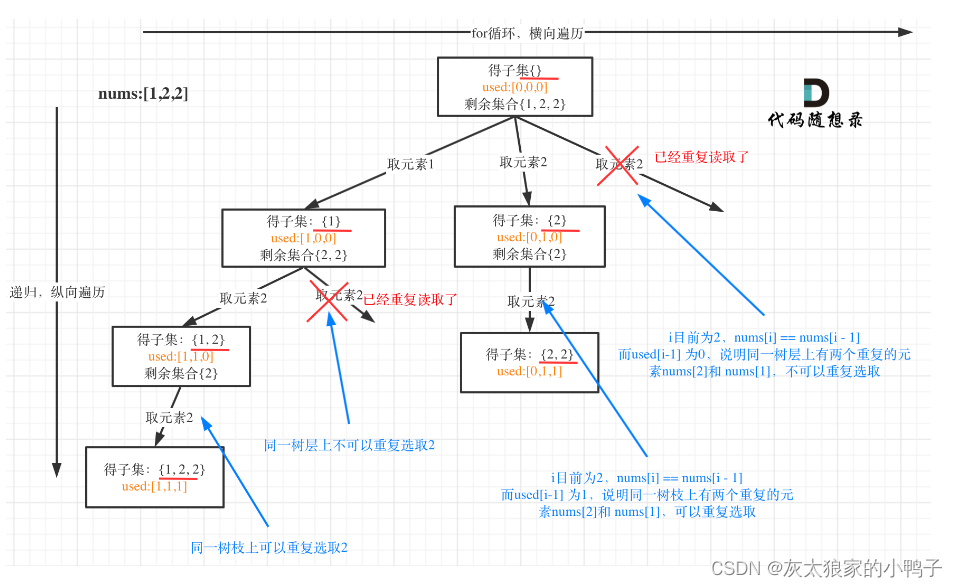
解析：这道题就是子集的问题上加入了去重的逻辑。对同一树层进行去重，树枝不去重。used[i-1] =false 是同一树层使用过了；used[i-1] =true是同一树枝上使用过了。

其次，对于去重问题，重要的需要提前对数组进行排序的操作。

/**
     * 就是在子集的基础上加了去重的逻辑：
     * 对同一树层进行去重的逻辑：
     * @param nums
     * @return
     */
    List<List<Integer>> res=new ArrayList<>();
    List<Integer> set=new ArrayList<>();
    boolean [] used;
    public List<List<Integer>> subsetsWithDup(int [] nums){
        //去重问题先给nums排序：
        Arrays.sort(nums);
        used=new boolean[nums.length];//默认都为false

        if (nums.length == 0 || nums == null){
            res.add(new ArrayList<>(set));
            return  res;
        }
        backTracking(nums,0);
        return res;
    }
    public void backTracking(int [] nums, int startIndex){
        res.add(new ArrayList<>(set));
        //回溯终止条件：
        if (startIndex>=nums.length){
            return;
        }

        //单层回溯：
        for (int i=startIndex;i<nums.length;i++){
            //used[i-1] =True 是同一树枝用过的数；
            //used[i-1] =false 是同一层用过的数；
            if (i>0 && nums[i] == nums[i-1] && used[i-1] ==false){
                continue;
            }
            set.add(nums[i]);
            used[i]=true;
            backTracking(nums,i+1);//递归
            set.remove(set.size()-1);//回溯
            used[i]=false;
        }

    }

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/496843.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！