【DP】学习之背包问题

news2024/9/27 21:25:36

01背包

2. 01背包问题 - AcWing题库

记忆化搜索

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,m;
int v[N],w[N]; 
int res;
int mem[N][N];
int dfs(int x,int spv)
{
	if(mem[x][spv]) return mem[x][spv];
	if(x>n) return mem[x][spv]=0;
	if(spv>=v[x])
	{
		return mem[x][spv]=max(dfs(x+1,spv),dfs(x+1,spv-v[x])+w[x]);
	}else return mem[x][spv]=dfs(x+1,spv);
}
signed main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
	res=dfs(1,m);
	cout<<res;
	return 0;
}

 这里补个图，DFS是自顶向下推的

dp的递推是从下往上

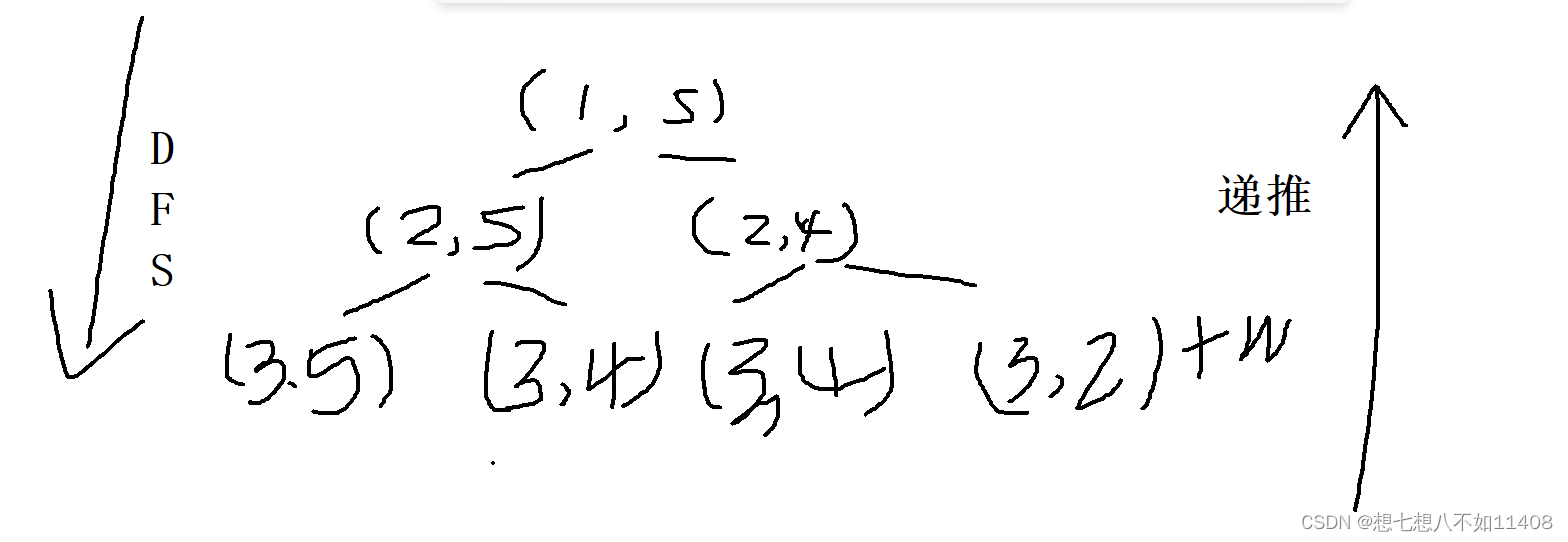 倒序递推

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,m;
int v[N],w[N]; 
int res;
int mem[N][N];
int f[N][N];
int dfs(int x,int spv)
{
	if(mem[x][spv]) return mem[x][spv];
	if(x>n) return mem[x][spv]=0;
	if(spv>=v[x])
	{
		return mem[x][spv]=max(dfs(x+1,spv),dfs(x+1,spv-v[x])+w[x]);
	}else return mem[x][spv]=dfs(x+1,spv);
}
signed main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
//	res=dfs(1,m);
//	cout<<res;
	
//	倒序递推f[i][j]
//	从第i个物品开始，选总体积<=j的物品的总价值的最大值 
	for(int i=n;i>=1;i--)
	{
		for(int j=0;j<=m;j++)
		{
			if(j<v[i]) f[i][j]=f[i+1][j];
			else f[i][j]=max(f[i+1][j],f[i+1][j-v[i]]+w[i]);
		}
	} 
	cout<<f[1][m];
	return 0;
}

正序递推

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,m;
int v[N],w[N]; 
int res;
int mem[N][N];
int f[N][N];
int dfs(int x,int spv)
{
	if(mem[x][spv]) return mem[x][spv];
	if(x<1) return mem[x][spv]=0;
	if(spv>=v[x])
	{
		return mem[x][spv]=max(dfs(x-1,spv),dfs(x-1,spv-v[x])+w[x]);
	}else return mem[x][spv]=dfs(x-1,spv);
}
signed main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
//	res=dfs(n,m);
//	cout<<res;
	
//	正序递推f[i][j]
//	从前i个物品中选，选总体积<=j的物品的总价值的最大值 
	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<=m;j++)
		{
			if(j<v[i]) f[i][j]=f[i-1][j];
			else f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]);
		}
	} 
	cout<<f[n][m];
	return 0;
}

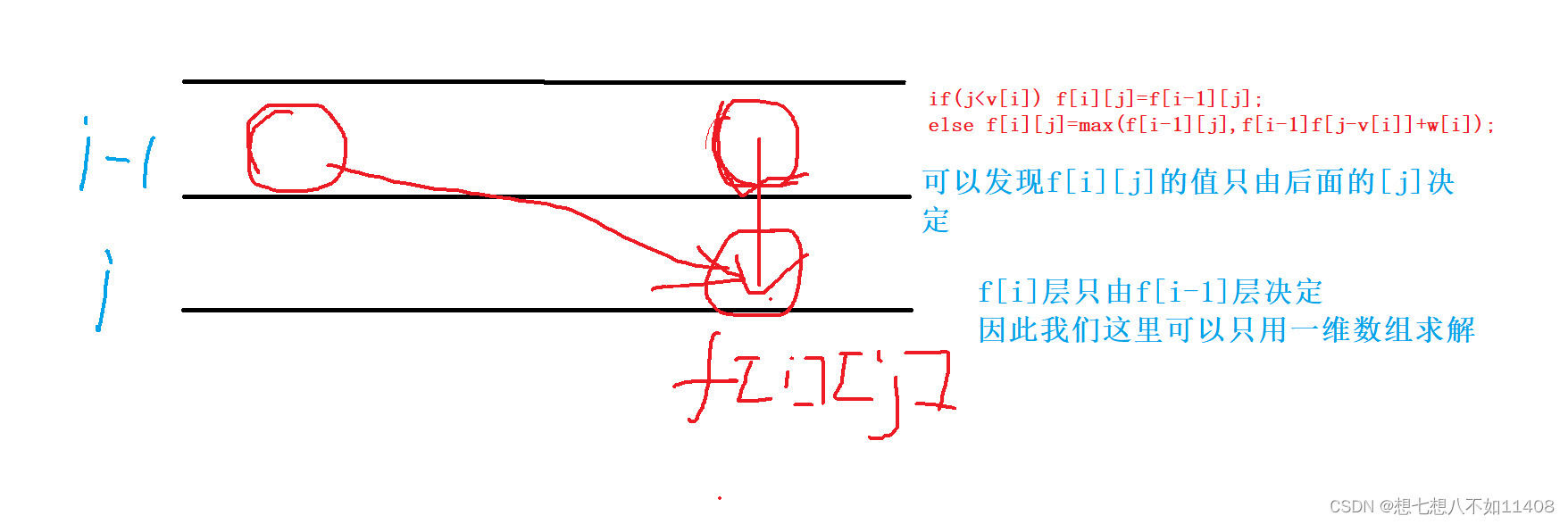
空间优化递推

用一维数组代替二维数组 

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,m;
int v[N],w[N]; 
int res;

int f[N],g[N];
signed main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];

	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<=m;j++)
		{
			if(j<v[i]) g[j]=f[j];
			else g[j]=max(f[j],f[j-v[i]]+w[i]);
		}
		memcpy(f,g,sizeof(f));
	} 
	cout<<f[m];
	return 0;
}

进一步优化

这里m从m走到0，的原因是只让每个物品最多拿一次。

如果正序枚举体积，就会让物品被拿多次，从而违反规则，

但完全背包不用考虑这个问题，因为它本身就能拿多次~

所以完全背包优化到一维可以正序枚举。

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,m;
int v[N],w[N]; 
int res;

int f[N];
signed main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];

	for(int i=1;i<=n;i++)
	{
		for(int j=m;j>=0;j--)
		{
            //if(j<v[i])  f[j]=f[j];//可以省略
			if(j>=v[i]) f[j]=max(f[j],f[j-v[i]]+w[i]);
		}
	} 
	cout<<f[m];
	return 0;
}

二维费用背包问题(本质是01背包）

8. 二维费用的背包问题 - AcWing题库

记忆化搜索

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,cap,we;
int v[N],m[N],w[N];
int mem[N][110][110];
int dfs(int x,int spv,int spm)
{
    if(mem[x][spv][spm]) return mem[x][spv][spm];
    
    if(x>n) return 0;
    if(spv>=v[x]&&spm>=m[x]) return mem[x][spv][spm]=max(dfs(x+1,spv,spm),dfs(x+1,spv-v[x],spm-m[x])+w[x]);
    else return mem[x][spv][spm]=dfs(x+1,spv,spm);
}
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n>>cap>>we;
    for(int i=1;i<=n;i++) cin>>v[i]>>m[i]>>w[i];
    int res=dfs(1,cap,we);
    cout<<res;
    return 0;
}

倒序递推

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,cap,we;
int v[N],m[N],w[N];
int mem[N][110][110];
int f[N][110][110];
int dfs(int x,int spv,int spm)
{
    if(mem[x][spv][spm]) return mem[x][spv][spm];
    
    if(x>n) return 0;
    if(spv>=v[x]&&spm>=m[x]) return mem[x][spv][spm]=max(dfs(x+1,spv,spm),dfs(x+1,spv-v[x],spm-m[x])+w[x]);
    else return mem[x][spv][spm]=dfs(x+1,spv,spm);
}
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n>>cap>>we;
    for(int i=1;i<=n;i++) cin>>v[i]>>m[i]>>w[i];
    // int res=dfs(1,cap,we);
    // cout<<res;
    for(int i=n;i>=1;i--)
    {
        for(int j=0;j<=cap;j++)
        {
            for(int k=0;k<=we;k++)
            {
                if(j<v[i]||k<m[i])
                {
                    f[i][j][k]=f[i+1][j][k];
                }
                else f[i][j][k]=max(f[i+1][j][k],f[i+1][j-v[i]][k-m[i]]+w[i]);
            }
        }
    }
    cout<<f[1][cap][we];
    return 0;
}

正序+二维优化

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,cap,we;
int v[N],m[N],w[N];
int mem[N][110][110];
int f[110][110];
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n>>cap>>we;
    for(int i=1;i<=n;i++) cin>>v[i]>>m[i]>>w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=cap;j>=v[i];j--)
        {
            for(int k=we;k>=m[i];k--)
            {
               f[j][k]=max(f[j][k],f[j-v[i]][k-m[i]]+w[i]);
            }
        }
    }
    cout<<f[cap][we];
    return 0;
}

完全背包

3. 完全背包问题 - AcWing题库

记忆化搜索

完全背包   和      01背包唯一不同就在于如果当前这个物品可以装入，在下一次选择中x不用+1（因为物品是无限多的，还可以再次选择）

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;

int n,m;
int v[N],w[N];
int mem[N][N];
int dfs(int x,int spv)
{
    if(mem[x][spv]) return mem[x][spv];
    if(x>n) return 0;
    if(spv<v[x])  return mem[x][spv]=dfs(x+1,spv);
    else return mem[x][spv]=max(dfs(x+1,spv),dfs(x,spv-v[x])+w[x]);
}
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    int res=dfs(1,m);
    cout<<res;
    return 0;
}

正序递推 

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;

int n,m;
int v[N],w[N];
int f[N][N];

int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            if(j<v[i]) f[i][j]=f[i-1][j];
            else f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i]);
        }
    }
    cout<<f[n][m];
    return 0;
}

优化成一维数组 

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;

int n,m;
int v[N],w[N];
int f[N];

int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=v[i];j<=m;j++)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]) ;
        }
    }
    cout<<f[m];
    return 0;
}

01   背包优化到一维      ：逆序枚举体积

完全背包优化到一维      ：正序枚举体积

习题

云剪贴板 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

NASA的食物计划（二维费用背包问题）

P1507 NASA的食物计划 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

记忆化搜索

#include<bits/stdc++.h>
using namespace std;
const int N=60;
int hh,tt,n;
int h[N],t[N],k[N];
int mem[55][410][510];
int dfs(int x,int sph,int spt)
{
	if(x>n) return 0;
	if(mem[x][sph][spt]) return mem[x][sph][spt];
	if(sph>=h[x]&&spt>=t[x])
	{
		return mem[x][sph][spt]=
		max(dfs(x+1,sph,spt),dfs(x+1,sph-h[x],spt-t[x])+k[x]);
	}else return mem[x][sph][spt]=dfs[x+1][sph][spt];
}
signed main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>hh>>tt>>n;
	for(int i=1;i<=n;i++) cin>>h[i]>>t[i]>>k[i];
	int res=dfs(1,hh,tt);
	cout<<res;

	return 0;
}

优化后的二维数组递推

#include<bits/stdc++.h>
using namespace std;
const int N=60;
int hh,tt,n;
int h[N],t[N],k[N];
int f[410][510];
signed main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>hh>>tt>>n;
	for(int i=1;i<=n;i++) cin>>h[i]>>t[i]>>k[i];
	for(int i=1;i<=n;i++)
	{
		for(int j=hh;j>=h[i];j--)
		{
			for(int l=tt;l>=t[i];l--)
			{
				f[j][l]=max(f[j][l],f[j-h[i]][l-t[i]]+k[i]);
			}
		}
	}
	cout<<f[hh][tt];
	return 0;
}

01背包求体积恰好为M的方案数

278. 数字组合 - AcWing题库

记忆化搜索

 Time Limit Exceeded   

要优化成递推

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int n,m;
int a[N];
int mem[N][10010];
int dfs(int x,int spm)
{
	if(spm==0) return 1;
	if(x>n) return 0;
	if(mem[x][spm]) return mem[x][spm];
	if(spm>=a[x]) return mem[x][spm]=dfs(x+1,spm-a[x])+dfs(x+1,spm);
	else return mem[x][spm]=dfs(x+1,spm);
}
signed main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i];
	int res=dfs(1,m);
	cout<<res;
	return 0;
}

一维数组递推

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int n,m;
int a[N];
int f[10010];//记录方案数 
signed main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i];
	
    f[0]=1;
	for(int i=1;i<=n;i++)
	{
		for(int j=m;j>=a[i];j--)
		{
			f[j]=f[j-a[i]]+f[j];
		}
	}
	cout<<f[m]; 
	return 0;
}

完全背包求体积恰好为M的方案数

OpenJudge - 6049:买书

记忆化搜索

这个就能ac了

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int n;
int mon[5]={0,10,20,50,100};
int mem[N][N];
int dfs(int x,int spn)
{
	if(spn==0) return 1;
	if(x>4) return 0;
	if(mem[x][spn]) return mem[x][spn];
	if(spn>=mon[x]) return mem[x][spn]=dfs(x+1,spn)+dfs(x,spn-mon[x]);
	else return mem[x][spn]=dfs(x+1,spn);
}
signed main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n;
	if(n==0)
	{
		cout<<"0";
		return 0;
	}
	int res=dfs(1,n);
	cout<<res;
	return 0;
}

优化一下

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int n;
int mon[5]={0,10,20,50,100};
int f[N];

signed main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n;
	if(n==0)
	{
		cout<<"0";
		return 0;
	}
	f[0]=1;
	for(int i=1;i<=4;i++)
	{
		for(int j=mon[i];j<=n;j++)
		{
			f[j]=f[j]+f[j-mon[i]];
		}
	}
	cout<<f[n];
	return 0;
}

背包问题求具体方案

12. 背包问题求具体方案 - AcWing题库

采药

P1048 [NOIP2005 普及组] 采药 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

疯狂的采药

P1616 疯狂的采药 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

5倍经验日

P1802 5 倍经验日 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

宠物小精灵之收服

OpenJudge - 4978:宠物小精灵之收服

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/496840.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

国内免费使用gpt-4-如何接入ChatGPT4

国内免费使用gpt-4-如何接入ChatGPT4

如何用上gpt-4 GPT-4尚未正式发布和公开&#xff0c;因此我们无法提供对GPT-4的具体使用方法。但是&#xff0c;可以从GPT-4的前一代——GPT-3的使用经验和GPT-4的预期功能来看&#xff0c;建议如下&#xff1a; 了解GPT-4的语言处理能力和适用场景&#xff1a;GPT-4预计将进一…
阅读更多...
项目实现读写分离操作（mysql）

项目实现读写分离操作（mysql）

读写分离 1.问题说明 2.读写分离 Master&#xff08;主库&#xff09;----(数据同步)—> Slave&#xff08;从库&#xff09; Mysql主从复制 mysql主从复制 介绍 mysql主从复制是一个异步的复制过程&#xff0c;底层是基于mysql数据库自带的二进制日志功能。就是一台或多台…
阅读更多...
【C语言】数组讲解

【C语言】数组讲解

【C语言】数组讲解 1.一维数组的创建和初始化1.1一维数组的创建1.2一维数组的初始化1.3一维数组的使用1.4一维数组在内存中的存储 2.二维数组的创建和初始化2.1二维数组的创建2.2二维数组的初始化2.3二维数组的使用2.4一维数组在内存中的存储 3.数组越界4.数组作为函数参数4.1冒…
阅读更多...
Mysql第四章 分库分表，读写分离，主从架构

Mysql第四章 分库分表，读写分离，主从架构

这里写自定义目录标题 一 分库分表1 为什么要分库分表2 分库分表的几种方式2.1 垂直拆分2.1.1 表的垂直拆分2.1.2库的垂直拆分2.1.2 垂直拆分的特点 2.2 水平拆分2.2.1 表的水平拆分2.2.2 库的水平拆分2.2.3 水平拆分的特点 3 分库分表的技术选型3.1 JDBC直连层3.2 proxy代理层…
阅读更多...
RocketMQ安装以及源码启动

RocketMQ安装以及源码启动

RocketMQ是一款消息中间件&#xff0c;在我们项目中主要是使用它来进行异步处理业务以及进行解耦&#xff0c;当然还可以用它实现其他业务需求比如流削峰等等&#xff0c;它提供的功能特别多&#xff0c;比如延迟消费、定时消费、消息重试、顺序消费等等。它的整体设计是追求简…
阅读更多...
基于Session实现短信验证码登录流程

基于Session实现短信验证码登录流程

文章目录 1 发送短信验证码与登录2 登录拦截功能3 隐藏用户敏感信息4 问题: 多台Tomcat的session共享问题 分析一下流程 发送验证码&#xff1a; 用户在提交手机号后&#xff0c;会校验手机号是否合法&#xff0c;如果不合法&#xff0c;则要求用户重新输入手机号 如果手机号…
阅读更多...
Django后端-短信验证码登录

Django后端-短信验证码登录

前端我使用的是vben-admin&#xff08;悄悄说一下&#xff0c;好难用。。&#xff09;&#xff0c;对原生的登录页进行了修改。 本文主要讲一下后端实现。 参考文档&#xff1a; djangocelery使用阿里云短信服务异步发送注册验证码_小泽十一章的博客-CSDN博客 django-实现登录…
阅读更多...
单链表OJ题：LeetCode--203.移除链表元素

单链表OJ题：LeetCode--203.移除链表元素

朋友们、伙计们&#xff0c;我们又见面了&#xff0c;今天给大家带来的是LeetCode中203题&#xff1a;移除链表元素 数据结构&#xff1a;数据结构专栏 作 者&#xff1a;stackY、 C 语 言 &#xff1a;C语言专栏 LeetCode--203.移除链表元素&#xff1a;https://leetco…
阅读更多...
攻防世界-web-simple js

攻防世界-web-simple js

题目描述&#xff1a;小宁发现了一个网页&#xff0c;但却一直输不对密码。(Flag格式为 Cyberpeace{xxxxxxxxx} ) 打开链接&#xff1a; 然后我们会发现不管我们输入什么密码&#xff0c;发现是都是这样的报错 1. 先用bp抓包看看&#xff0c;可以抓到这样的一串js脚本 看不懂…
阅读更多...
SVM（基于李航统计学习方法，包含SMO）

SVM（基于李航统计学习方法，包含SMO）

文章目录 线性可分SVM和硬间隔最大化函数间隔和几何间隔间隔最大化支持向量 学习的对偶算法 线性SVM和软间隔最大化支持向量 非线性SVM和核函数SMO算法求解二次规划选择变量第一个变量第二个变量 计算 b b b 和 E i E_i Ei​ 线性可分SVM和硬间隔最大化 函数间隔和几何间隔 …
阅读更多...
C++11多线程：std::thread创建线程和std::async创建异步任务的区别，std::async创建异步任务后没有被推迟执行。

C++11多线程：std::thread创建线程和std::async创建异步任务的区别，std::async创建异步任务后没有被推迟执行。

系列文章目录 文章目录 系列文章目录前言一、thread和async的区别1.1 新线程和异步任务1.2 std::async和std::thread最明显的不同&#xff0c;就是async有时候并不创建新线程。1.3 std::async和std::thread的区别1.4 std::async不确定性问题的解决 二、使用方法2.1 std::async创…
阅读更多...
js基础内容

js基础内容

第一种,几乎完全不用 <a href"#" onclick"alert(百度一下)">百度一下</a>第二种,写在script内 <body><a class"baidu" href"#">百度一下</a><script>var baiduAEldocument.querySelector("…
阅读更多...
ChatGPT-5即将发布，上千名人士却紧急叫停

ChatGPT-5即将发布，上千名人士却紧急叫停

ChatGPT4还没有好好体验&#xff0c;比GPT4强大1000倍的ChatGPT5又即将发布&#xff01;届时将彻底改变人工智能领域&#xff0c;并改变我们现有的世界 【ChatGPT 5简介】 OpenAI计划在2023年12月发布其最新且最强大的人工智能模型——ChatGPT 5。该模型具备人工通用智能的能力…
阅读更多...
中文大模型安全性哪家强？清华团队新发布

中文大模型安全性哪家强？清华团队新发布

当前大型语言模型的火爆程度我们不用再进行赘述了&#xff0c;伴随着百度文心一言打响国内商业大模型第一枪&#xff0c;华为盘古&#xff0c;阿里通义千问&#xff0c;智谱ChatGLM,科大讯飞星火等国内公司纷纷开始布局。 另一方面由于众所周知的政策原因&#xff0c;和如火如荼…
阅读更多...
Threejs进阶之十三：CSS3DRenderer与Tween.js实现粒子小球按规律变化

Threejs进阶之十三：CSS3DRenderer与Tween.js实现粒子小球按规律变化

今天我们使用CSS3DRendererTween.js实现Threejs官方示例中的粒子小球按规律变化的效果&#xff0c;先看下最终实现的效果 先来分析下&#xff0c;这个页面的动画效果是由512个小球组合起来的四种不同变化&#xff0c;分别是曲面、立方体、随机和圆球四种变化&#xff1b;下面我…
阅读更多...
Linux——进程间通信(管道)

Linux——进程间通信(管道)

目录 进程通信的目的 管道 见见猪跑(举个例子) 文件描述符fd与管道的关系(深度理解管道) 什么是管道&#xff1f; 匿名管道 pipe函数概述 父子进程通信时与文件描述符的关系图(理解pipe函数的关键) pipe函数的使用 管道读写规则 管道的大小 自测 使用man 7 pipe查看 …
阅读更多...
Unity Timeline使用

Unity Timeline使用

Unity Timeline使用 1.创建Timeline&#xff1a;打开面板Window->Sequencing->Timeline (1.1)选择一个要添加 Timeline 的物体&#xff0c;我创建一个物体就叫 Timeline(可以随意命名)&#xff0c;选择Timeline&#xff0c;然后在面板上显示 Create 按钮&#xff0c;如…
阅读更多...
Arduino_STM32 之Arduino IDE开发配置

Arduino_STM32 之Arduino IDE开发配置

前言 由于选了物联网作为选修课&#xff0c;老师喜欢使用Arduino进行编程&#xff0c;但是也要教我们使用STM32。于是他就让我们使用Arduino IDE开发STM32&#xff08;用Keil 不好吗&#xff1f;&#xff1f;&#xff1f;&#xff09;。 第一章 软件下载 安装Arduino IDE&…
阅读更多...
springboot请求响应

springboot请求响应

SpringBootWeb请求响应 前言 在上一次的课程中&#xff0c;我们开发了springbootweb的入门程序。 基于SpringBoot的方式开发一个web应用&#xff0c;浏览器发起请求 /hello 后 &#xff0c;给浏览器返回字符串 “Hello World ~”。 其实呢&#xff0c;是我们在浏览器发起请求…
阅读更多...
环形链表 力扣

环形链表 力扣

题目描述 题目要求 判断一个单链表是不是环形链表&#xff0c;是就返回true 不是就返回false 思路 要搞清楚环形链表长啥样环形链表有哪些特征 环形链表顾名思义就是在链表中有一个类似环形的结构&#xff0c; 它和普通单链表的区别就是 你用遍历普通单链表的法子遍历一个环…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023