1、最少城市数

【题目】

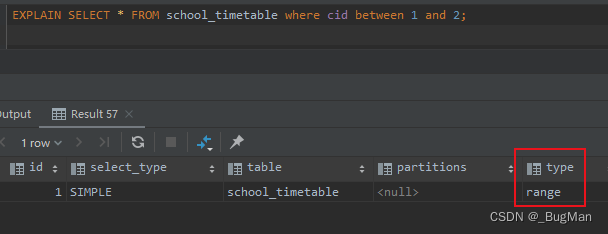
下图表示的是从城市A到城市H的交通图。从图中可以看出，从城市A到城市H要经过若干个城市。现要找出一条经过城市最少的一条路线。

【算法分析】

看到这图很容易想到用邻接距阵来表示，0表示能走，1表示不能走。如图。

首先想到的是用队列的思想。q数组是存储扩展结点的队列，q[i]记录经过的城市,b[i]记录前趋城市，这样就可以倒推出最短线路。具体过程如下：

（1）将城市A入队，队首为0、队尾为1。（2）将队首所指的城市所有可直通的城市入队（如果这个城市在队列中出现过就不入队，可用一布尔数组visited[i]来判断），将入队城市的前趋城市保存在b[i]中。然后将队首加1，得到新的队首城市。重复以上步骤，直到搜到城市H时，搜索结束。利用b[i]可倒推出最少城市线路。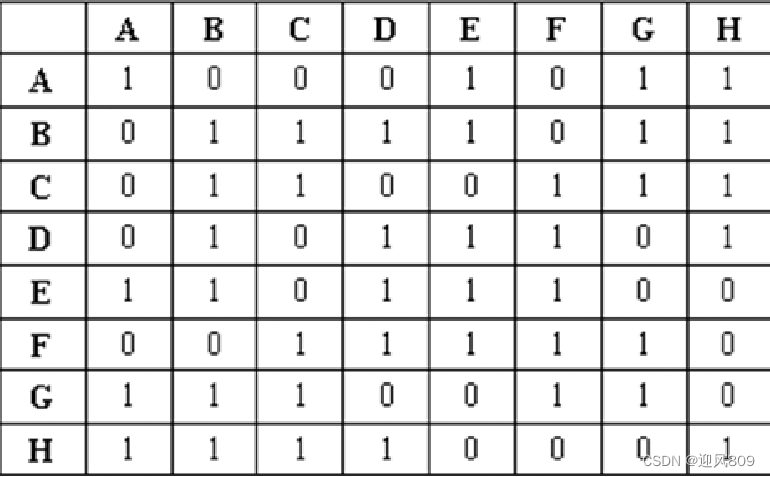

【运行代码】

#include <bits/stdc++.h>
using namespace std;
int Map[9][9]={{0,0,0,0,0,0,0,0,0},
                    {0,1,0,0,0,1,0,1,1},
                    {0,0,1,1,1,1,0,1,1},
                    {0,0,1,1,0,0,1,1,1},
                    {0,0,1,0,1,1,1,0,1},
                    {0,1,1,0,1,1,1,0,0},
                    {0,0,0,1,1,1,1,1,0},
                    {0,1,1,1,0,0,1,1,0},
                    {0,1,1,1,1,0,0,0,1}};

bool visited[10];
int q[100];
int b[100];
int main()
{
    int flag=0;
    int head=0,tail=0;
    q[++tail]=1;//初始化使A进队，A-H用1-8的数字表示
    visited[1]=1;
    //广搜！搜索队列！！
    while(head<=tail)
    {
        head++;
        cout<<"当前的q[head]="<<q[head]<<endl;;
        for(int j=1;j<=8;j++)
        if(Map[q[head]][j]==0&&visited[j]==0)
        {

            q[++tail]=j;
             cout<<"tail="<<tail<<","<<char(q[tail]+64)<<",";
            if(visited[tail]==0) b[tail]=head;//记录第j个城市的前驱是第i个城市,并且记录的是这个城市的第一个遇到的前驱
            visited[j]=1;
            cout<<"前驱是"<<char(head+64)<<endl;
            if(j==8)
            {
                flag=1;break;
            }
        }
        if(flag==1) break;
    }
    int i=8;
    int ans=1;
    cout<<char(q[i]+64);
    while(b[i]!=0)
    {
        i=b[i];
        ans++;
        cout<<"--"<<char(q[i]+64);

    }
    cout<<"\n总共经过"<<ans<<"个城市";

}