( “ 图 “ 之并查集 ) 684. 冗余连接 —

( “ 图 “ 之并查集 ) 684. 冗余连接 ——【Leetcode每日一题】

news2024/11/18 5:30:32

❓684. 冗余连接

难度：中等

树可以看成是一个连通且无环的无向图。

给定往一棵 n 个节点 (节点值 1～n ) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

示例 1：

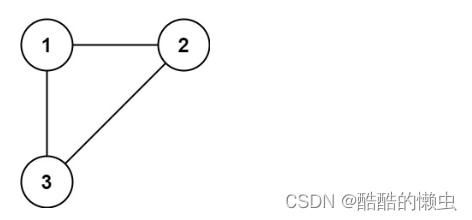
在这里插入图片描述

输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：

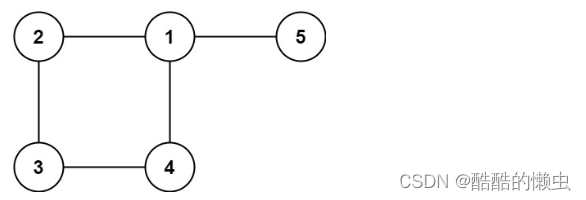
在这里插入图片描述

输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

提示:

n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <= edges.length
ai != bi
edges 中无重复元素
给定的图是连通的

💡思路：并查集

树是一个连通且无环的无向图，在树中多了一条附加的边之后就会出现环，因此附加的边即为导致环出现的边。

可以通过并查集寻找附加的边。并查集可以动态地连通两个点，并且可以非常快速地判断两个点是否连通。

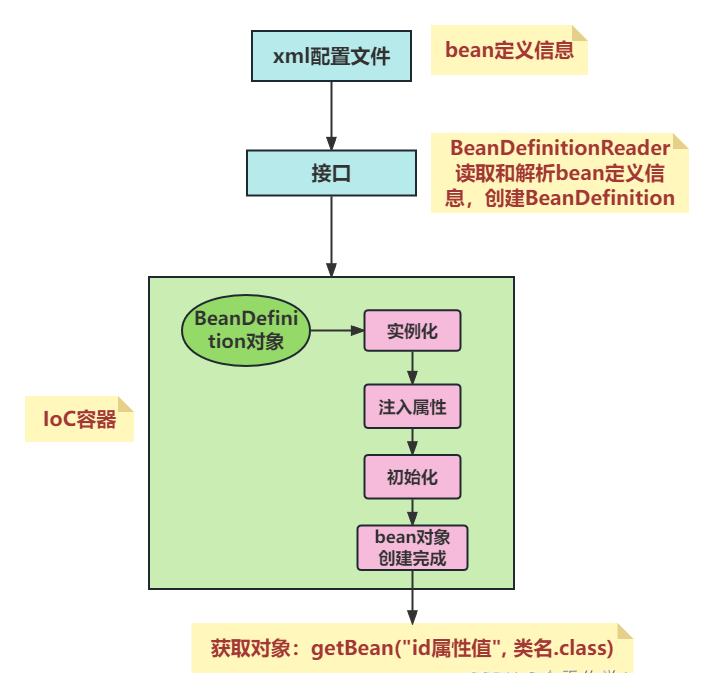
并查集的基本思想是维护一个森林，每个集合对应一棵树，树的根节点表示该集合的代表元素。初始时，每个元素都是一个单独的集合，对应一棵只包含自己的树。合并操作可以将两棵树合并为一棵树，查找操作可以找到某个元素所在的树的根节点。

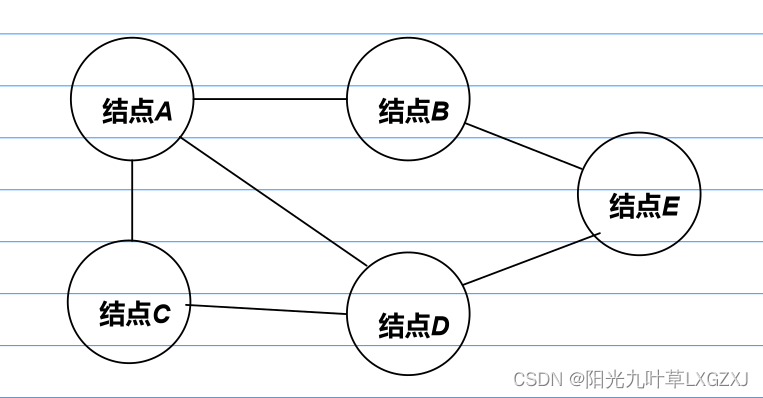
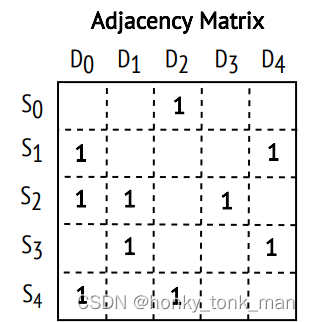
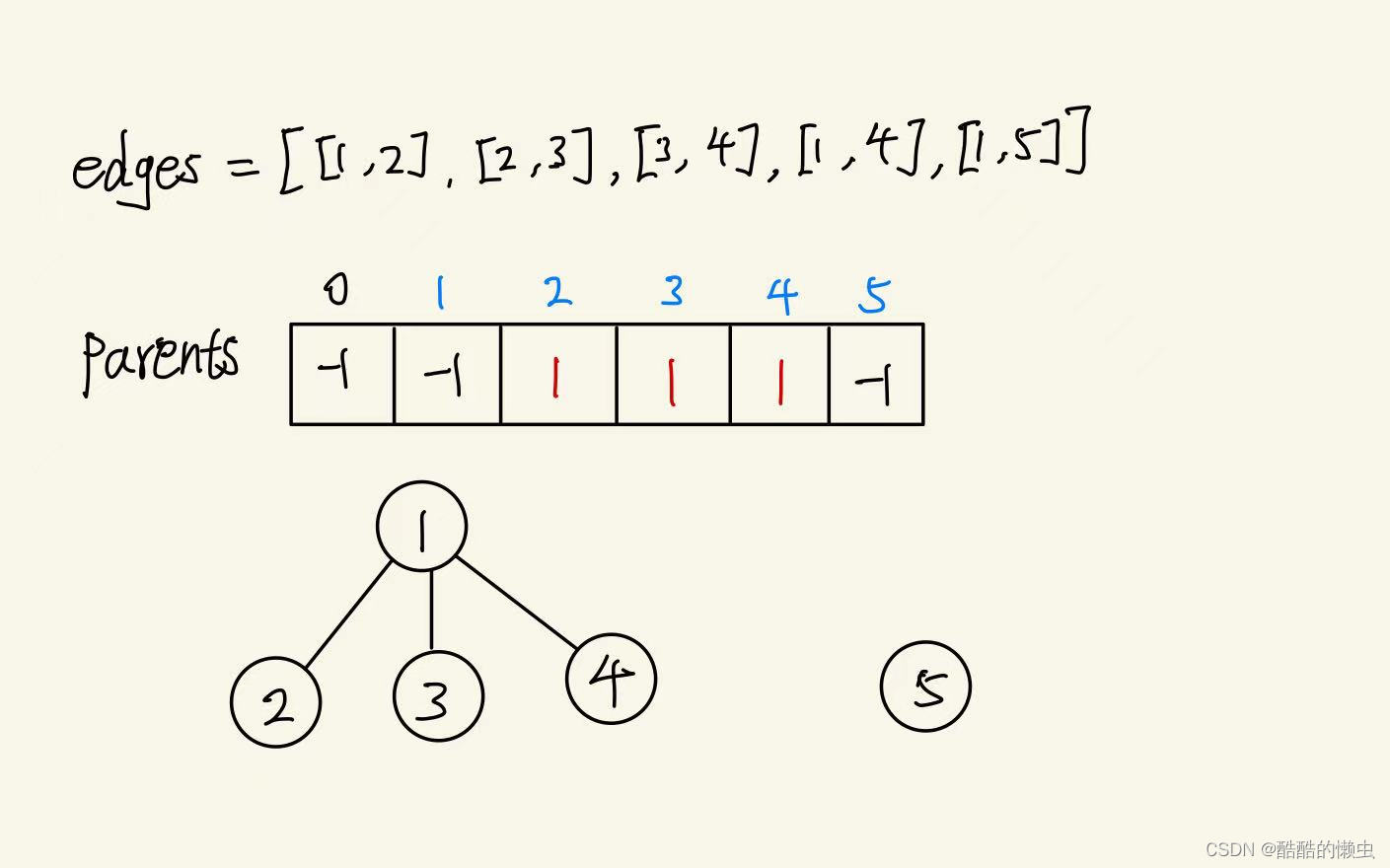
我们可以使用一个一位数组parents存储每个节点的根节点，即根节点的数组下标，以例2举例，如下图：

在这里插入图片描述

并查集最主要的是就是以下两种操作：

查找操作：查找某个元素所属的集合，即查找该元素所在数的根节点（祖先）。
合并操作：将两个集合合并为一个集合，祖先不同，则合并：
- 合并时可以通过路径压缩来优化时间复杂，就是如果两个根节点的深度不同，就让深度小的根节点的祖先等于深度较大的节点，从而使整颗树不会太深，查找祖先时间不会太长，平均时间为 $O (l o g n)$ 。

🍁代码：(Java、C++)

Java

class Solution {
    private int[] ans = new int[2];
    public int[] findRedundantConnection(int[][] edges) {
        int n = edges.length;
        int[] parents = new int[n + 1];//存储每个节点的父节点
        Arrays.fill(parents, -1);
        int[] heigh = new int[n + 1];//存储根节点的深度
        for(int[] edge: edges){//遍历所有的边
            if(!t_Union(edge[0], edge[1], parents, heigh)){
                break;
            }
        }
        return ans;
    }
    private int find_Root(int root, int[] parents){//查找到根节点（祖先）
        while(parents[root] != -1){
            root = parents[root];
        }
        return root;
    }
    private boolean t_Union(int x, int y, int[] parents, int[] heigh){//合并
        int x_root = find_Root(x, parents);//如果根节点相同，则存在环，合并失败
        int y_root = find_Root(y, parents);
        if(x_root == y_root){
            ans[0] = x;
            ans[1] = y;
            return false;
        }else if(heigh[x_root] > heigh[y_root]){//将深度小的合并到深度大的根节点上
            parents[y_root] = x_root;
        }else if(heigh[x_root] < heigh[y_root]){
            parents[x_root] = y_root;
        }else{
            parents[y_root] = x_root;
            heigh[x_root]++;
        }
        return true;
    }
}

C++

class Solution {
public:
    vector<int> ans;
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        int n = edges.size();
        vector<int> parents(n + 1, -1);//存储每个节点的父节点
        vector<int> heigh(n + 1, 0);//存储根节点的深度
        for(auto edge : edges){//遍历所有的边
            if(!t_Union(edge[0], edge[1], parents, heigh)) break;
        }
        return ans;
    }
    int find_Root(int root, vector<int>& parents){//查找到根节点（祖先）
        while(parents[root] != -1){
            root = parents[root];
        }
        return root;
    }
    bool t_Union(int x, int y, vector<int>& parents, vector<int>& heigh){//合并
        int x_root = find_Root(x, parents);
        int y_root = find_Root(y, parents);
        if(x_root == y_root){//如果根节点相同，则存在环，合并失败
            ans.push_back(x);
            ans.push_back(y);
            return false;
        }else if(heigh[x_root] > heigh[y_root]){//将深度小的合并到深度大的根节点上
            parents[y_root] = x_root;
        }else if(heigh[x_root] < heigh[y_root]){
            parents[x_root] = y_root;
        }else{
            parents[y_root] = x_root;
            heigh[x_root]++;
        }
        return true;
    }
};

🚀 运行结果：

在这里插入图片描述

🕔 复杂度分析：

时间复杂度： $O (n l o g n)$ ，其中 n 是图中的节点个数，需要遍历图中的 n 条边，对于每条边，需要对两个节点查找祖先，如果两个节点的祖先不同则需要进行合并，需要进行 2 次查找和最多 1 次合并。一共需要进行 2n 次查找和最多 n 次合并，因此总时间复杂度是 $O (2 n l o g n)$ = $O (n l o g n)$ 。
空间复杂度： $O (n)$ ，其中 n 是图中的节点个数，使用数组 parents 记录每个节点的祖先。