k近邻法（k-nearest neighbor, k-NN)是一种基本分类与回归方法（下面只写分类的）

knn的输入为实例的特征向量，对应于特征空间的店；
输出为实例的类别。
knn假设给定的训练数据集，其中的实力类别已定，分类时，对新的实例，根据其k个最近邻的训练实例的类别，通过多数表决等方式进行预测。

算法

输入：训练数据集
T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯   , ( x N , y N ) } T = \left\{\left(\mathbf{x}_1,y_1\right), \left(\mathbf{x}_2,y_2\right), \cdots, \left(\mathbf{x}_N,y_N\right)\right\} T={(x1​,y1​),(x2​,y2​),⋯,(xN​,yN​)}
其中 x i ∈ X ⊆ R n , y i ∈ Y = { c 1 , c s , ⋯   , c K } \mathbf{x}_i\in \mathcal{X} \subseteq \mathbb{R}^n, y_i \in \mathcal{Y}=\left\{c_1, c_s, \cdots,c_K\right\} xi​∈X⊆Rn,yi​∈Y={c1​,cs​,⋯,cK​},这里大写的$K$表示类别，和knn的$k$没有关系
输出：实例$\mathbf{x}$所属的类$y$
(1)根据给定的距离度量，在训练集$T$中找出与$\mathbf{x}$最近的$k$个店，涵盖这$k$个点的$\mathbf{x}$的领域记作$N_k\left(\mathbf{x}\right)$
(2)在$N_k\left(\mathbf{x}\right)$中根据分类决策规则（如多数表决）决定$\mathbf{x}$的类别$y$
$$y=\arg \underset{c_j}{\max }\sum _{{\mathbf{x}}_i\in N_k\left(\mathbf{x}\right)}I\left(y_i=c_j\right),i=1,2,c\dots ,N;j=1,2,\cdots ,K$$
其中$I$是指示函数，$y_i=c_j$时为$1$，其他时候为$0$

kd树

由于线性扫描比较耗时，所以用kd树

构造

输入：$k$维空间数据集 T = { x 1 , ⋯   , x N } T=\left\{\mathbf{x}_1, \cdots, \mathbf{x}_N\right\} T={x1​,⋯,xN​}(注意这里的这个k和knn的k没有关系)
其中${\mathbf{x}}_i={\left({\mathbf{x}}_i^{\left(1\right)},\cdots ,{\mathbf{x}}_i^{\left(k\right)}\right)}^T$
输出：kd树
（1）开始：构造根节点，根节点对应于包含$T$的$k$维空间的超矩形区域
选择${\mathbf{x}}^{\left(1\right)}$为坐标轴，以$T$中所有的实例的${\mathbf{x}}^{(1)}$坐标的中位数为切分点，将根节点对应的超矩形区域切分为两个子区域。

由根节点生成深度为1的左、右子节点：左子节点对应坐标${\mathbf{x}}^{(1)}$小于切分点的子区域，右子节点对应于坐标${\mathbf{x}}^{(1)}$大于切分点的子区域

（2）重复：对深度为$j$的节点，选择${\mathbf{x}}^{\left(l\right)}$为切分的坐标轴，$l=j\left(\mathrm{mod}k\right)+1$,以该节点的区域中所有实例的${\mathbf{x}}^{(l)}$坐标的中位数为切分点，将该节点对应的超矩形区域切分为两个子区域。

由该节点生成深度为$j+1$的左、右子节点：左子节点对应坐标${\mathbf{x}}^{(l)}$小于切分点的子区域，右子节点对应于坐标${\mathbf{x}}^{(l)}$大于切分点的子区域

(3)直到两个子区域没有实例存在时停止，从而形成kd树的区域划分

补充：
找中位数，可以使用C++的nth_element，也就是快排里的partition

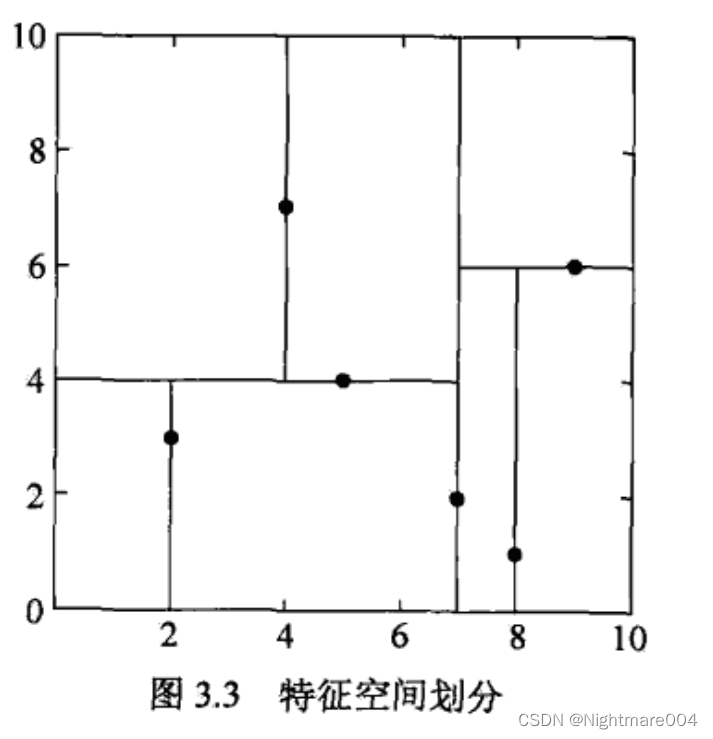
搜索

假设寻找$\mathbf{x}\in {\mathbb{R}}^k$的$k$个最近邻
(1)设$L$为一个有 $k$个空位的列表，用于保存已搜寻到的最近点。
(2)根据$\mathbf{x}$的坐标值和每个节点的切分向下搜索
(3)当达叶子节点时，如果$L$里不足$k$个点，则将当前节点的特征坐标加入$L$；如果$L$不为空并且当前节点的特征与$\mathbf{x}$的距离小于$L$里最长的距离，则用当前特征替换掉$L$中离$\mathbf{x}$最远的点。
(4)如果当前节点不是整棵树根节点，执行 (a)；反之，输出$L$，算法完成。
(a) 向上一层（当前节点的父节点）执行1和2。

1. 如果此时$L$里不足$k$个点，则将节点特征加入$L$；如果$L$中已满$k$个点，且当前节点与$\mathbf{x}$的距离小于$L$里最长的距离，则用节点特征替换掉$L$中离最远的点。
2. 计算$\mathbf{x}$和当前节点切分线的距离。如果该距离大于等于$L$中距离$\mathbf{x}$最远的距离并且$L$中已有$k$个点，则在切分线另一边不会有更近的点，执行 (4)；如果该距离小于$L$中最远的距离或者$L$中不足$k$个点，则切分线另一边可能有更近的点，因此在当前节点的另一个孩子中从 (2) 开始执行。

这里(4)-(a)-2说的切分线的距离，指：设根据第$l$个维度切分，那么计算$x^{(l)}$和切分线的距离
因此选的距离，应该是类似$L_p$这种，这样如果距离大于等于$L$中距离$\mathbf{x}$最远的距离并且$L$中已有$k$个点，另一个区域中的点${\mathbf{x}}_i$才能满足$d\left(\mathbf{x},{\mathbf{x}}_i\right)\ge \left|x^{(l)}-x_i^{(l)}\right|$，进而舍弃这些点

代码

#!/usr/bin/env python
# _*_ coding:utf-8 _*_
from collections import Counter

import numpy as np
import heapq

import matplotlib
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split


def distance(x, y):
    return np.sqrt(np.sum((x.squeeze() - y.squeeze()) ** 2))


class KDNode:
    def __init__(self, data=None, label=None, split_dim=None, split_val=None, left=None, right=None):
        self.data = data  # shape(n,)
        self.label = label  # shape(1,)
        self.split_dim = split_dim
        self.split_val = split_val
        self.left = left
        self.right = right


class KDTree:
    def __init__(self, k, distance):
        self.root = None
        self.k = k
        self.distance = distance

    def _build_tree(self, X, Y, l, r, depth):
        split_dim = depth % X.shape[1]
        if l + 1 == r:
            return KDNode(X[l], Y[l], split_dim, X[l, split_dim])
        elif l >= r:
            return None

        # mid = l + (r - l) // 2
        mid = (l + r - 1) // 2
        partition = l + np.argpartition(X[l:r, split_dim], mid - l)
        X[l:r] = X[partition]
        Y[l:r] = Y[partition]
        split_val = X[mid, split_dim]
        root = KDNode(X[mid], Y[mid], split_dim, split_val)
        root.left = self._build_tree(X, Y, l, mid, depth + 1)
        root.right = self._build_tree(X, Y, mid + 1, r, depth + 1)
        return root

    def build_tree(self, X, Y):
        self.root = self._build_tree(X, Y, 0, X.shape[0], 0)

    def _search(self, x, root: KDNode, ans: list, k: int):
        if not root:
            return
        elif root.left is None and root.right is None:
            dist = self.distance(root.data, x)
            if len(ans) < k:
                # the id(root) here is to prevent heapq comparing the data and the label, because it is not comparable
                heapq.heappush(ans, (-dist, id(root), root.data, root.label))
            elif len(ans) == k and -dist > ans[0][0]:  # dist1 < dist_max
                heapq.heapreplace(ans, (-dist, id(root), root.data, root.label))
            return
        split_dim = root.split_dim

        next_root, other_root = None, None
        if x[split_dim] < root.split_val:
            next_root = root.left
            other_root = root.right
        else:
            next_root = root.right
            other_root = root.left

        self._search(x, next_root, ans, k)

        dist = self.distance(root.data, x)
        if len(ans) < k:
            heapq.heappush(ans, (-dist, id(root), root.data, root.label))
        elif len(ans) == k and -dist > ans[0][0]:  # dist1 < dist_max
            heapq.heapreplace(ans, (-dist, id(root), root.data, root.label))
        if other_root is not None and np.abs(x[split_dim] - root.split_val) < -ans[0][0]:
            self._search(x, other_root, ans, k)

    def search(self, x):
        ans = []
        self._search(x.squeeze(), self.root, ans, self.k)
        # ans.sort(key=lambda cur: -cur[0])
        return [cur[2:] for cur in ans]


class KNN:
    def __init__(self, k, distance):
        self.kd_tree = KDTree(k, distance)

    def fit(self, X, Y):
        self.kd_tree.build_tree(X, Y)

    def predict_one(self, x):
        """

        :param x: x.shape=(n,)
        :return:
        """
        k_list = self.kd_tree.search(x)
        # print(k_list)
        cnt = Counter()
        for p, y in k_list:
            cnt.update({y: 1})
            # weighted by 1/ distance
            # cnt.update({y: 1.0 / distance(x, p)})
        return cnt.most_common(1)[0][0]

    def predict(self, X):
        return np.array([self.predict_one(x) for x in X], dtype=np.int64)


if __name__ == '__main__':
    # X = np.array([
    #     [6.27, 5.50],
    #     [1.24, -2.86],
    #     [17.05, -12.79],
    #     [-6.88, -5.40],
    #     [-2.96, -0.50],
    #     [7.75, -22.68],
    #     [10.80, -5.03],
    #     [-4.60, -10.55],
    #     [-4.96, 12.61],
    #     [1.75, 12.26],
    #     [15.31, -13.16],
    #     [7.83, 15.70],
    #     [14.63, -0.35]
    # ])
    # Y = np.random.randint(0, 2, X.shape[0])
    # print(X)
    # print(Y)
    # knn = KNN(3, distance)
    # knn.fit(X, Y)
    # print(knn.predict(np.array([[-1, -5], [-1, -5]])))

    iris = load_iris()
    X = iris.data[:, :2]  # (150,2)
    Y = iris.target  # (150,)
    X_train, X_test, y_train, y_test = train_test_split(X, Y, stratify=Y, random_state=42)

    n_neighbors = 5
    knn = KNN(5, distance)
    knn.fit(X_train, y_train)
    y_pred = knn.predict(X_test)
    print(y_pred)
    # 查看各项得分
    print("y_pred", y_pred)
    print("y_test", y_test)
    # print("score on train set", knn.score(X_train, y_train))
    # print("score on test set", knn.score(X_test, y_test))
    print("accuracy score", accuracy_score(y_test, y_pred))


    # 可视化
    # 自定义colormap
    def colormap():
        return matplotlib.colors.LinearSegmentedColormap.from_list('cmap', ['#FFC0CB', '#00BFFF', '#1E90FF'], 256)


    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    axes = [x_min, x_max, y_min, y_max]
    xp = np.linspace(axes[0], axes[1], 500)  # 均匀500的横坐标
    yp = np.linspace(axes[2], axes[3], 500)  # 均匀500个纵坐标
    xx, yy = np.meshgrid(xp, yp)  # 生成500X500网格点
    xy = np.c_[xx.ravel(), yy.ravel()]  # 按行拼接，规范成坐标点的格式
    y_pred = knn.predict(xy).reshape(xx.shape)  # 训练之后平铺

    # 可视化方法一
    # plt.figure(figsize=(15, 5), dpi=100)
    plt.contourf(xx, yy, y_pred, alpha=0.3, cmap=colormap())
    # 画三种类型的点
    p1 = plt.scatter(X[Y == 0, 0], X[Y == 0, 1], color='blue', marker='^')
    p2 = plt.scatter(X[Y == 1, 0], X[Y == 1, 1], color='green', marker='o')
    p3 = plt.scatter(X[Y == 2, 0], X[Y == 2, 1], color='red', marker='*')
    # 设置注释
    plt.legend([p1, p2, p3], iris['target_names'], loc='upper right', fontsize='large')
    # 设置标题
    plt.title(f"3-Class classification (k = {n_neighbors})", fontdict={'fontsize': 15})
    plt.show()

参考：
统计学习方法(李航)
https://zhuanlan.zhihu.com/p/23966698
https://bitbucket.org/StableSort/play/src/master/src/com/stablesort/kdtree/KDTree.java
https://zhuanlan.zhihu.com/p/343657182