数据结构与算法基础-学习-23-图之邻接矩阵与邻接表

news2024/11/18 6:01:02

目录

一、定义和术语

二、存储结构

1、邻接矩阵

1.1、邻接矩阵优点

1.2、邻接矩阵缺点

2、邻接表

3、邻接矩阵和邻接表的区别和用途

3.1、区别

3.2、用途

三、宏定义

四、结构体定义

1、邻接矩阵

2、邻接表

3、网数据类型（造测试数据）

五、函数定义

1、使用邻接矩阵创建无向网

2、使用邻接表创建无向网

3、销毁使用邻接矩阵创建的无向网

4、销毁使用邻接表创建的无向网

六、Linux环境编译测试

一、定义和术语

名词描述
图Graph = ( Vertex , Edge )
Vertex:顶点（数据元素）的有穷非空集合。
Edge:边的有穷集合。
无向图每条边都是无方向的。
有向图每条边都是有方向的。
完全图任意两个点都有一条边相连。
无向完全图：n个顶点，n * (n - 1) / 2条边。
有向完全图：n个顶点，n * (n - 1)条边。
稀疏图有很少的边或弧的图。
稠密图有较多的边或弧的图。
网边/弧带权的图。
邻接有边/弧相连的两个顶点之间的关系。
存在(vi, vj)，则称vi和vj互为邻接点。
存在<vi, vj>，则称vi邻接到vj，vj邻接到vi。
关联（依附）边/弧与顶点之间的关系。
存在(vi, vj) / <vi, vj>，则称该边/弧关联于vi和vj。
顶点的度

于该顶点相关联的边的数目，记作TD(v),在有向图中，顶点的度等于该顶点的入度于出度之和。
顶点v的入度是以v为终点的有向边的条数，记作ID(v)。

顶点v的出度是以v为始点的有向边的条数，记作OD(v)。

有向树当有向图中仅一个顶点的入度为0，其余顶点的入度为1.
路径接续的边构成的顶点序列。
路径长度路径上边或弧的数目/权值之和。
回路（环）第一个顶点和最后一个顶点相同路径。
简单路径除路径起点和终点可以相同外，其余顶点均不相同的路径。
简单回路（简单环）除路径起点和终点相同外，其余顶点均不相同的路径。
连通图（强连通图）在无（有）向图G = (V, {E})中，若对任何两个顶点v，u都存在从v到u的路径，则称G是连通图（强连通图）。
权与网图中边或弧所具有的相关数称为权。表明从一个顶点到另一个顶点的距离或耗费。
带权的图称为网。
子图设有两个图G = (V, {E})、G1 = (V1, {E1})，V1∈V，E1∈E，则称G1是G的子图。
连通分量（强连通分量）无向图G的极大连通子图称为G的连通分量。
极大连通子图该子图是G的连通子图，将G的任何不在该子图中的顶点加入，子图不再是连通。
强连通分量有向图G的极大强连通子图称为G的强连通分量。
极大强连通子图该子图是G的强连通子图，将G的任何不在该子图中的顶点加入，子图不再是强连通。
极小连通子图该子图是G的连通子图，在该子图中删除任何一条边，子图不再连通。。
生成树包含无向图G所有顶点的极小连通子图。
生成森林对非连通图，由各个连通分量的生成树的集合。

二、存储结构

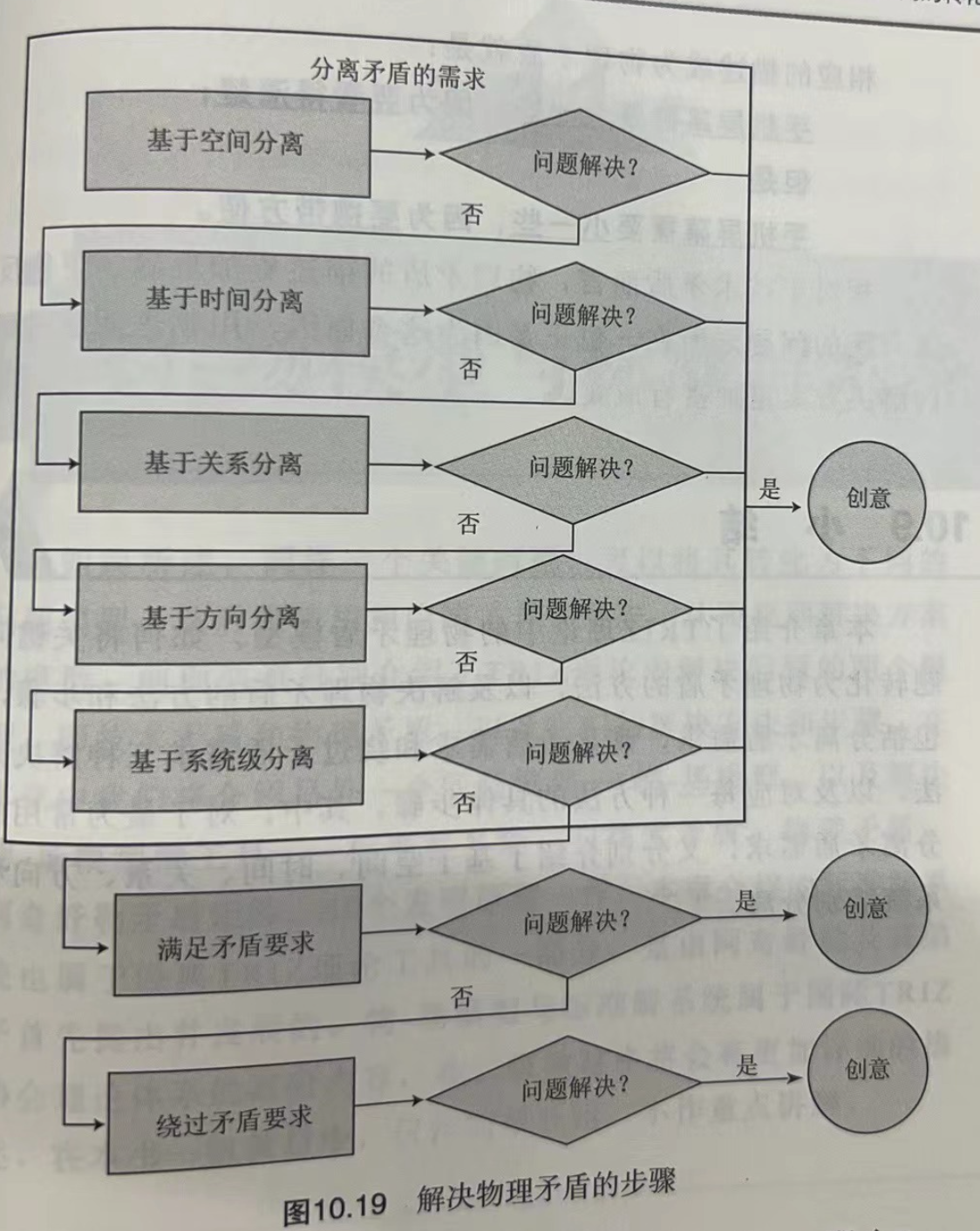
图的逻辑结构是多对多的，具体分类如下：

分类名描述
数组存储结构1、邻接矩阵。（本文介绍）
链式存储结构

1、邻接表。（本文介绍）

2、邻接多重表。

3、十字链表。

 这里以无向网为例，我们要画一个这样的。

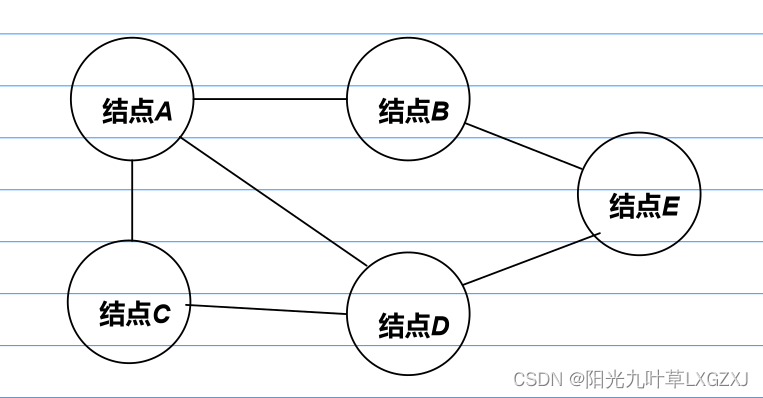
测试数据：

举例说明一下{0,3,10}，A->D且权值为10。

{'A','B','C','D','E'};
{{0,3,10},{0,1,20},{0,2,30},{2,3,10},{1,4,50},{3,4,20}};

1、邻接矩阵

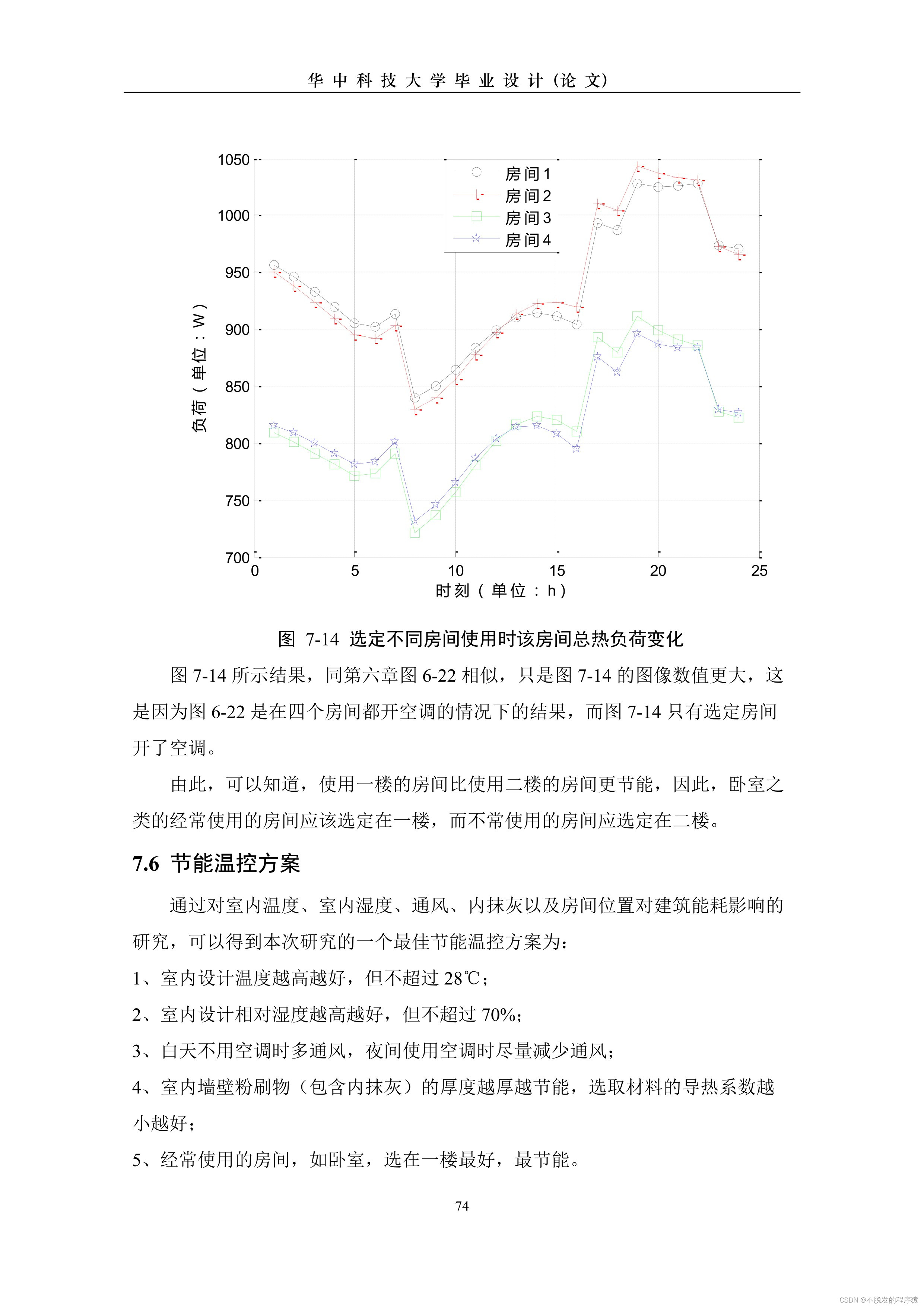
建立一个顶点表（记录各个顶点信息）和一个邻接矩阵（表示各个顶点之间关系）。

生成的邻接矩阵如下：

VertexArray    : [A ,B ,C ,D ,E ]
ArcArray       :
[32767 ,20    ,30    ,10    ,32767 ]
[20    ,32767 ,32767 ,32767 ,50    ]
[30    ,32767 ,32767 ,10    ,32767 ]
[10    ,32767 ,10    ,32767 ,20    ]
[32767 ,50    ,32767 ,20    ,32767 ]

[32767 ,20    ,30    ,10    ,32767 ]第一行表示：A->A不通，A->B通，A->C通，A->D通，A->E不通。

特性1：无向网的邻接矩阵是对称的。

特性2：顶点i的度等于第i行中非极大值（32767）的个数。

特别：完全网的邻接矩阵中，对角元素为32767，其余皆为非32767。

1.1、邻接矩阵优点

（1）直观好理解。

（2）容易判断两个顶点间是否存在边或弧。

（3）容易查找任意顶点的所有邻接点。

（4）方便计算任意顶点的度。

1.2、邻接矩阵缺点

（1）添加和删除顶点不方便。

（2）存储稀疏图时浪费空间。

（3）统计稀疏图一共有多少条边浪费时间。

2、邻接表

顶点：按编号顺序将顶点数据存储在一维数组中。

关联同一顶点的边（以顶点为尾的弧）：用线性链表存储。

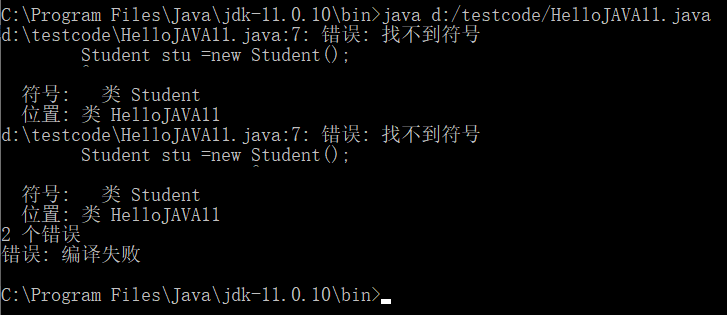
生成的邻接表如下：

A : [ (2, 30, 0x15ac8b0),(1, 20, 0x15ac870),(3, 10, (nil))]
B : [ (4, 50, 0x15ac8d0),(0, 20, (nil))]
C : [ (3, 10, 0x15ac910),(0, 30, (nil))]
D : [ (4, 20, 0x15ac950),(2, 10, 0x15ac890),(0, 10, (nil))]
E : [ (3, 20, 0x15ac990),(1, 50, (nil))]

A : [ (2, 30, 0x15ac8b0),(1, 20, 0x15ac870),(3, 10, (nil))]第一行表示：A->C通、权值30、下一个结点指针，A->B通、权值20、下一个结点指针，A->D通、权值10、下一个结点指针。

特性1：邻接表不唯一。

特性2：若无向网中有n个顶点、e条边，则其邻接表需要n个头结点和2e个表结点。存储稀疏图比较合适。

特性3：无向网中顶点Vi的度为第i个单链表中的结点数。

特性4：邻接表出度易找，入度难找。逆邻接表出度难找，入度易找。

3、邻接矩阵和邻接表的区别和用途

3.1、区别

（1）对于任一确定的无向网，邻接矩阵是唯一的（行列号与顶点编号一致），但邻接表不唯一。

（2）邻接矩阵的空间复杂度是O(n^2)，邻接表为O(n+e)。

3.2、用途

邻接矩阵多用于稠密图。

邻接表多用于稀疏图。

三、宏定义

#define MAX_INT_TYPE_NUM      32767 //网中代表无穷大，也代表顶点个数。
#define MAX_VERTEX_NUM        10000 //顶点数组中存放顶点的最大个数。
#define NET_DIRECTION_FLAG    0     //有向网的标志
#define NET_UNDIRECTION_FLAG  1     //无向网的标志

四、结构体定义

1、邻接矩阵

//邻接矩阵图
typedef struct AdjacencyMatrixGraph
{
    VertexType VertexArray[MAX_VERTEX_NUM];
    ArcType    ArcArray[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
    int        CurVertexNum; //顶点数组中当前的顶点数。
    int        CurArcNum;    //弧数组中当前的弧个数。
}AMGraph;

2、邻接表

//邻接表
typedef struct ArcNode
{
    VertexIndexType EndVertexIndex;
    WeightType      Weight;
    struct ArcNode* NextNodePtr;
}ArcNode;

typedef struct VertexNode
{
    VertexType Vertex;
    ArcNode*   FirstArcNodePtr;
}VertexNode;

typedef struct AdjacencyGragh
{
    VertexNode* Vertices;
    int         VertexNum;        //邻接表中的顶点数。
    int         ArcNum;           //邻接表中的弧个数。        
}AGraph;

3、网数据类型（造测试数据）

//网数据类型
typedef struct NetArcDataType
{
    VertexIndexType StartVertexIndex;//起始顶点。
    VertexIndexType EndVertexIndex;  //结束顶点。
    WeightType      Weight;          //权值。
}NetArcDataType;                     //数据为网的弧或边的信息。

// NetArcDataType  NetArcDataArray[MAX_VERTEX_NUM * (MAX_VERTEX_NUM - 1)]。
// 问题简记，如果MAX_VERTEX_NUM为1000时，在malloc NetDataType*类型内存时，会出现段错误。
typedef struct NetDataType
{
    VertexType*     VertexArray;
    NetArcDataType* NetArcDataArray;  //有向图完全图的边最多，顶点n,边最多为n*(n-1)。
    int             VertexNum;        //顶点数据数组中的顶点数。
    int             ArcNum;           //弧数据数组中的弧个数。
    int             DirectionFlag;    //无向图还是有向图的标志。
}NetDataType;                         //数据为网的信息。

五、函数定义

1、使用邻接矩阵创建无向网

Status CreateUndirectionNetUseAMGraph(AMGraph** AMG, NetDataType NDT)
{
    *AMG = (AMGraph*)MyMalloc(sizeof(AMGraph));    

    int i,j;

    (*AMG)->CurVertexNum = NDT.VertexNum;  //顶点数复制。
    (*AMG)->CurArcNum    = NDT.ArcNum * 2; //边数复制，由于无向图是双向的，所以需要乘2。
        
    //顶点数组复制。
    memcpy((*AMG)->VertexArray, NDT.VertexArray, sizeof(VertexType) * ((*AMG)->CurVertexNum));

    //初始化网中弧或边数组，统一初始化为无穷大，这里设置为int的最大值32767。
    for(i = 0; i < (*AMG)->CurVertexNum; i++)
    {
        for(j = 0; j < (*AMG)->CurVertexNum; j++)
        {   
            (*AMG)->ArcArray[i][j] = MAX_INT_TYPE_NUM;
        }
    }

    //把网数据中的弧或边数据填充到邻接矩阵图中。
    for(i = 0; i < NDT.ArcNum; i++)
    {
        (*AMG)->ArcArray[NDT.NetArcDataArray[i].StartVertexIndex][NDT.NetArcDataArray[i].EndVertexIndex] = NDT.NetArcDataArray[i].Weight;
        (*AMG)->ArcArray[NDT.NetArcDataArray[i].EndVertexIndex][NDT.NetArcDataArray[i].StartVertexIndex] = NDT.NetArcDataArray[i].Weight;
    }
    Log("Create Undirection Net Use AMGraph : OK\n",Info);
    return SuccessFlag;
}

2、使用邻接表创建无向网

Status CreateUndirectionNetUseAGraph(AGraph** AG, NetDataType NDT)
{
    (*AG) = (AGraph*)MyMalloc(sizeof(AGraph));

    (*AG)->VertexNum = NDT.VertexNum;
    (*AG)->ArcNum    = NDT.ArcNum * 2;

    //init adjacency graph
    (*AG)->Vertices = (VertexNode*)MyMalloc(sizeof(VertexNode) * (*AG)->VertexNum);
    int i;
    for(i = 0; i < (*AG)->VertexNum; i++)
    {
        (*AG)->Vertices[i].Vertex          = NDT.VertexArray[i];
        (*AG)->Vertices[i].FirstArcNodePtr = NULL;
    }

    //add arc to adjacency graph
    ArcNode* TmpArcNode  = NULL;
    for(i = 0; i < NDT.ArcNum; i++)
    {
        //printf("%d, %d, %d\n",NDT.NetArcDataArray[i].StartVertexIndex,NDT.NetArcDataArray[i].EndVertexIndex,NDT.NetArcDataArray[i].Weight);
        ArcNode* NewArcNode        = (ArcNode*)MyMalloc(sizeof(ArcNode));
        NewArcNode->EndVertexIndex = NDT.NetArcDataArray[i].EndVertexIndex;
        NewArcNode->Weight         = NDT.NetArcDataArray[i].Weight;
        NewArcNode->NextNodePtr    = NULL;

        TmpArcNode = (*AG)->Vertices[NDT.NetArcDataArray[i].StartVertexIndex].FirstArcNodePtr;
        if(TmpArcNode == NULL)//说明弧结点链表头部为空
        {
            (*AG)->Vertices[NDT.NetArcDataArray[i].StartVertexIndex].FirstArcNodePtr = NewArcNode;
        }
        else
        {
            NewArcNode->NextNodePtr                                                  = TmpArcNode;
            (*AG)->Vertices[NDT.NetArcDataArray[i].StartVertexIndex].FirstArcNodePtr = NewArcNode; //头插法,效率高。
        }

        ArcNode* NewArcNode1        = (ArcNode*)MyMalloc(sizeof(ArcNode));
        NewArcNode1->EndVertexIndex = NDT.NetArcDataArray[i].StartVertexIndex;
        NewArcNode1->Weight         = NDT.NetArcDataArray[i].Weight;
        NewArcNode1->NextNodePtr    = NULL;

        TmpArcNode = (*AG)->Vertices[NDT.NetArcDataArray[i].EndVertexIndex].FirstArcNodePtr;
        if(TmpArcNode == NULL)//说明弧结点链表头部为空
        {
            (*AG)->Vertices[NDT.NetArcDataArray[i].EndVertexIndex].FirstArcNodePtr = NewArcNode1;
        }
        else
        {
            NewArcNode1->NextNodePtr                                               = TmpArcNode;
            (*AG)->Vertices[NDT.NetArcDataArray[i].EndVertexIndex].FirstArcNodePtr = NewArcNode1;
        }
    }
    Log("Create Undirection Net Use AGraph  : OK\n",Info);
    return SuccessFlag;
}

3、销毁使用邻接矩阵创建的无向网

Status DestoryUndirectionNetUseAMGraph(AMGraph** AMG)
{
    JudgeAllNullPointer(AMG);
    JudgeAllNullPointer(*AMG);
    free(*AMG);
    *AMG = NULL;
    Log("Destory Undirection Net Use AMGraph: OK\n",Info);
    return SuccessFlag;
}

4、销毁使用邻接表创建的无向网

Status DestoryUndirectionNetUseAGraph(AGraph** AG)
{
    JudgeAllNullPointer(AG);
    JudgeAllNullPointer(*AG);

    ArcNode* TmpArcNode = NULL;
    ArcNode* CurArcNode = NULL;   

    //free All ArcNode
    int i;
    for(i = 0; i < (*AG)->VertexNum; i++)
    {
        (*AG)->Vertices[i].Vertex = '\0';
        TmpArcNode = (*AG)->Vertices[i].FirstArcNodePtr;
        CurArcNode = TmpArcNode;
        while(CurArcNode != NULL)
        {
            TmpArcNode = CurArcNode->NextNodePtr;
            free(CurArcNode);
            CurArcNode = TmpArcNode;
        }
    }
    
    //free VertexNode
    free((*AG)->Vertices);
    (*AG)->Vertices = NULL;

    //free AGraph
    (*AG)->VertexNum = 0;
    (*AG)->ArcNum    = 0;
    free(*AG);    
    *AG              = NULL;

    Log("Destory Undirection Net Use AGraph : OK\n",Info);
    return SuccessFlag;
}

六、Linux环境编译测试

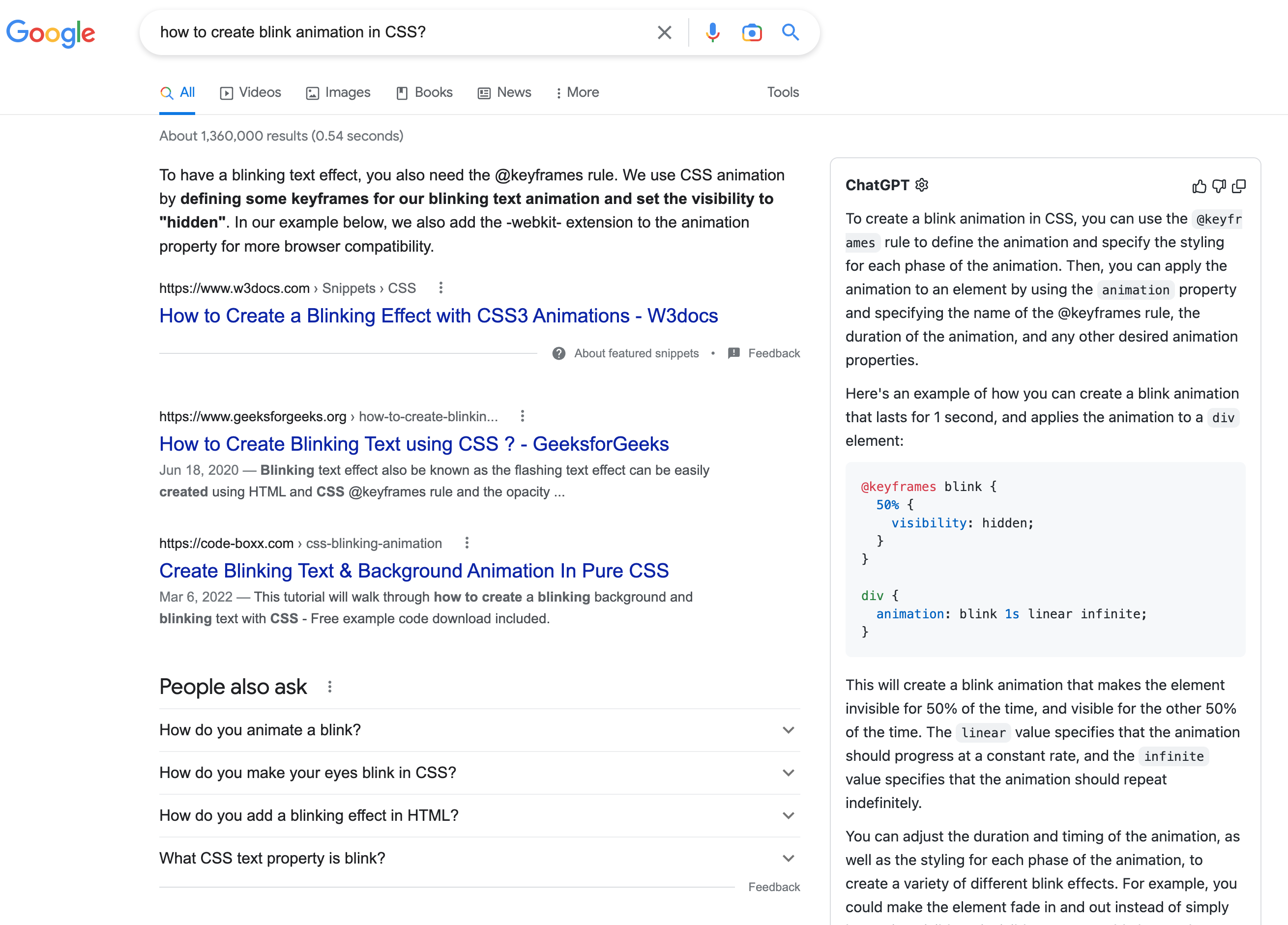
[gbase@czg2 Graph]$ make
gcc -Wall -Wextra -g ../Log/Log.c ../PublicFunction/PublicFunction.c ../PublicFunction/SqQueue/SqQueue.c Graph.c main.c -o TestGraph -I ../Log/ -I ../PublicFunction/ -I ../Select/ -I ../PublicFunction/SqQueue/

[gbase@czg2 Graph]$ ./TestGraph 
[2023-5]--[ Info  ]--Create Net Data                    : OK
[2023-5]--[ Info  ]--Create Undirection Net Use AMGraph : OK
[2023-5]--[ Debug ]--Printf AMGraph                     :
VertexArray    : [A ,B ,C ,D ,E ]
ArcArray       :
[32767 ,20    ,30    ,10    ,32767 ]
[20    ,32767 ,32767 ,32767 ,50    ]
[30    ,32767 ,32767 ,10    ,32767 ]
[10    ,32767 ,10    ,32767 ,20    ]
[32767 ,50    ,32767 ,20    ,32767 ]
CurVertexNum   : 5
CurArcNum      : 12
[2023-5]--[ Info  ]--Create Undirection Net Use AGraph  : OK
[2023-5]--[ Debug ]--Printf AGraph                      :
A : [ (2, 30, 0xe078b0),(1, 20, 0xe07870),(3, 10, (nil))]
B : [ (4, 50, 0xe078d0),(0, 20, (nil))]
C : [ (3, 10, 0xe07910),(0, 30, (nil))]
D : [ (4, 20, 0xe07950),(2, 10, 0xe07890),(0, 10, (nil))]
E : [ (3, 20, 0xe07990),(1, 50, (nil))]
VertexNum      : 5
ArcNum         : 12

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/496468.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何使用TRIZ理论来分析问题和解决问题？

如何使用TRIZ理论来分析问题和解决问题？

文章目录 TRIZ基础现代TRIZ步骤 TRIZ基础 现代TRIZ 经典的TRIZ方法对专利进行分析,认为专利分为两个部分,一部分是需要解决的问题,一部分是解决问题的解决方案.首先是问题的分析,确定是否是初始问题,比如工具功能分析/特性传递等工具. 步骤 问题识别 主要是识别出初始问题;…
阅读更多...
MATLAB实现建筑热平衡模型建立及节能温控方案

MATLAB实现建筑热平衡模型建立及节能温控方案

全球大约1/3的能源消耗于建筑。在能源紧张的今天&#xff0c;如何减少建筑的能源浪费是一个值得研究的课题。 本文在综合国内外建筑能耗模拟方法的基础上&#xff0c;采用热平衡法&#xff0c;针对一小型建筑建立了热特性仿真模型&#xff0c;选用武汉地区的气象数据&#xff…
阅读更多...
JAVA11新特性

JAVA11新特性

JAVA11新特性 概述 2018年9月26日,Oracle官方发布JAVA11.这是JAVA大版本周期变化后的第一个长期支持版本,非常值得关注.最新发布的JAVA11将带来ZGC HttpClient等重要特性,一共17个需要我们关注的JEP,参考文档http://openjdk.java.net/projects/jdk/11/ 181:基于嵌套的访问控制…
阅读更多...
云计算适合大专生学吗？

云计算适合大专生学吗？

云计算适合大专生学吗&#xff1f; 对于大专毕业生来说&#xff0c;云计算的确是一个不错的选择&#xff0c;因为云计算技术应用专业&#xff0c;主要就是专科院校在办学。不管你是计算机相关专业的&#xff0c;还是零基础想学习都是可以的&#xff1b;原因就在于云计算这门专业…
阅读更多...
七款非常好用的 ChatGPT 开源插件

七款非常好用的 ChatGPT 开源插件

推荐7款很好用的 ChatGPT 开源插件 1. ChatGPT ProBot 这是一个基于chatGPT实现的Github机器人&#xff0c;可以让chatGPT帮你审核代码、重构代码&#xff0c;还可以在Github页面上和它进行聊天&#xff0c;咨询问题。 仓库地址: github.com/oceanlvr/Ch… 2.chatgpt-api 这…
阅读更多...
如何在本地部署运行ChatGLMS-6B

如何在本地部署运行ChatGLMS-6B

在本篇技术博客中&#xff0c;将展示如何在本地获取运行代码和模型&#xff0c;并配置环境以及 Web GUI&#xff0c;最后通过 Gradio 的网页版 Demo 进行聊天。 官方介绍 ChatGLM-6B 是一个开源的、支持中英双语的对话语言模型&#xff0c;基于 General Language Model (GLM)…
阅读更多...
图应用替换算法

图应用替换算法

文章目录 LRUSHiPBeladys MIN replacement(T-OPT)图应用基本知识CSR和CSCT-OPT替换算法使用 P-OPTRereference MatrixModified Rereference Matrix LRU 过于简单不做具体介绍 SHiP SHiP全称Signature-base Hit Predctor算法&#xff0c;其主打的是基于Signature(签名)进行Pr…
阅读更多...
flutter学习之旅 -有状态的组件(StatefulWidget)

flutter学习之旅 -有状态的组件(StatefulWidget)

文章目录 StatefulWidget格式实现num增加finalfinal定义数组 我们重建一个项目 flutter create 项目名我们会看到 在Flutter中自定义组件其实就是一个类&#xff0c;这个类需要继承StatelessWidget/StatefulWidget StatelessWidget是无状态组件&#xff0c;状态不可改变的widg…
阅读更多...
点成分享丨细胞培养三步骤——复苏、传代、冻存

点成分享丨细胞培养三步骤——复苏、传代、冻存

细胞培养是指在体外模拟生物体内环境&#xff08;无菌、适宜温度、酸碱度和一定营养条件等&#xff09;&#xff0c;使之生存、生长、繁殖并维持主要结构和功能的一种方法。 细胞培养也叫细胞克隆技术&#xff0c;是细胞生物学研究方法中重要和常用技术&#xff0c;通过细胞培…
阅读更多...
k近邻法学习

k近邻法学习

k近邻法&#xff08;k-nearest neighbor, k-NN)是一种基本分类与回归方法&#xff08;下面只写分类的&#xff09; knn的输入为实例的特征向量&#xff0c;对应于特征空间的店&#xff1b; 输出为实例的类别。 knn假设给定的训练数据集&#xff0c;其中的实力类别已定&#xf…
阅读更多...
使用vscode进行python的单元测试，提高开发效率

使用vscode进行python的单元测试，提高开发效率

背景知识 单元测试在我们的开发过程中非常有必要&#xff0c;它可以验证实现的一个函数是否达到预期。以前在学校写代码时&#xff0c;都是怼一堆代码&#xff0c;然后直接运行&#xff0c;如果报错再一步步调试&#xff0c;这样大部分时间都浪费在调试工作上。工作后发现大家…
阅读更多...
【c/c++】curl编译（CMake方式）

【c/c++】curl编译（CMake方式）

一、curl下载 下载地址&#xff1a;curl - Download 进入下载页面&#xff0c;选择Old Releases。 二、CMake下载 这玩意居然有官网&#xff0c;刷新了我的认知&#xff0c;省事啊。 Download | CMake 三、CMake生成VS项目 1、点击【Browse Source ...】&#xff0c;先选择…
阅读更多...
蓝牙耳机哪个品牌最好？数码博主整理2023超高性价比蓝牙耳机推荐

蓝牙耳机哪个品牌最好？数码博主整理2023超高性价比蓝牙耳机推荐

近来收到很多私信不知道蓝牙耳机哪个品牌最好&#xff0c;希望我能进行一期蓝牙耳机推荐&#xff0c;考虑到大家的预算不高&#xff0c;我特意花费时间测评了当下主流品牌的热销平价蓝牙耳机&#xff0c;最终整理成了这份超高性价比蓝牙耳机推荐&#xff0c;感兴趣的朋友们可以…
阅读更多...
ASN.1-PKCS10

ASN.1-PKCS10

ASN1采用一个个的数据块来描述整个数据结构&#xff0c;每个数据块都有四个部分组成&#xff1a; 1、数据块数据类型标识&#xff08;一个字节&#xff09; 数据类型包括简单类型和结构类型。 简单类型是不能再分解类型&#xff0c;如整型(INTERGER)、比特串(BIT STRING)、字…
阅读更多...
【Unity】搭建Jenkins打包工作流，远程打热更、构建App

【Unity】搭建Jenkins打包工作流，远程打热更、构建App

Jenkins是团队协作项目打包常用的工作流&#xff0c;不多做介绍。 Jenkins的部署Unity打包环境还是非常简单的&#xff1a; 工作流程如下&#xff1a; 1. 在Jenkins中添加打包配置参数(如: 版本号, 目标平台等), 参数将以UI的形式显示在Jenkins Web界面以便打包前填写参数&a…
阅读更多...
机器人抓取检测——Dex-Net

机器人抓取检测——Dex-Net

如今&#xff0c;在各种期刊顶会都能看到平面抓取检测的论文&#xff0c;他们声称能应对多物体堆叠场景&#xff0c;然而实际效果都不尽人意&#xff0c;我认为主要原因有如下几点&#xff1a; 缺乏多物体堆叠场景的抓取数据集。现在最常用的Cornell Grasp Dataset, Jacquard数…
阅读更多...
政务网中使用内部华为云

政务网中使用内部华为云

项目按甲方要求&#xff0c;部署在政务网&#xff0c;各种需要在系统中播放的视频存放于内部华为云&#xff1b;然后&#xff0c;系统需要在互联网上访问。 经过一天捣鼓&#xff0c;终于搞定。过程中遇到了许多问题&#xff0c;有nginx代理的&#xff0c;docker域名解析的&am…
阅读更多...
FTP Entering Extended Passive Mode

FTP Entering Extended Passive Mode

目录 原因 两种方法解决，哪个行用哪种 方法一 方法二 原因 FTP的连接建立有两种模式PORT
阅读更多...
10个优秀设计网站盘点

10个优秀设计网站盘点

从平面广告设计、包装设计和标志设计到游戏特效&#xff0c;都与我们的生活息息相关。过去&#xff0c;设计师依靠一张图纸和一支笔&#xff0c;但进入数字时代后&#xff0c;设计工作从图纸转移到了电脑上。 各种设计网站和在线设计工具相继衍生&#xff0c;简化了工作步骤&a…
阅读更多...
Packet Tracer - 配置扩展 ACL - 场景 1

Packet Tracer - 配置扩展 ACL - 场景 1

Packet Tracer - 配置扩展 ACL - 场景 1 拓扑图 地址分配表 设备 接口 IP 地址 子网掩码 默认网关 R1 G0/0 172.22.34.65 255.255.255.224 不适用 G0/1 172.22.34.97 255.255.255.240 不适用 G0/2 172.22.34.1 255.255.255.192 不适用 服务器 NIC 172.22.…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023