LRU

过于简单不做具体介绍

SHiP

SHiP全称Signature-base Hit Predctor算法，其主打的是基于Signature(签名)进行Predicr,未来这个Signature对应的Cache是否会被hit
SHiP算法需要额外添加三个部分，扩展Cache line新增2个field分别为signature_m和outcome，还有一个是额外的SHCT表

• signature_m:用于定位这个cache line再SHCT表中的位子
• outcome:初始化为0，当cache line被重复引用后置为1，0代表从始至初都没有被重复引用过
• SHCT:全称Signature History Counter Table，这个表记载了一个signature的重复引用的情况，当一个被evicted出cache的cache line，并且没有被重复引用，那么SHCT就会减去对应cache line对应的entry，假如hit(不在Cache 中会被引入到Cache中，在Cache中不会变)，那么就增加SHCT对应的entry

算法对应的伪代码如下

if hit then  //假设我们cpu下发的LDST指令操作的对象从cache中找到
	Cache_line.outcome = true; //将cache line对应的outcome field设置为true代表被re-reference，也就是被重复引用
	Increment SHCT[signature_m]; //increase SHCT中对应的cache line
else //cache miss,也就是cpu下发的LDST指令操作的对象没有从cache中找到
	if evicted_cache_line.outcome != true;  //这里其实要遍历SHCT中所有被evict且只被hit一次的cache，将他们对应的SHCT表项减一
		Decrement SHCT[signature_m];
	cache_line.outcome = false; //这里其实是本次hit的cache line是第一次hit，初始化对应的outcome
	cache_line.signature_m = signature; //同上,不过这里是初始化signature也就是在SHCT中给这个cache line分配一个SHCT的entry
	if SHCT[signature] == 0 //这里就是predict了假设SHCT为0说明我们这个cache被重用的概率非常低
		predict distant refrence;
	else //说明这个cache line有一定的被重用的概率，根据概率不同结合其他的替换算法进行排序比如LRU
		predict internediate re-refrence;
end if

有了上述的代码我们就很容易明白SHiP是个是个流程,我们只需要结合其他的替换算法即可，比如LRU，根据我们predict的re-refrence更改LRU的chain

图应用对SHiP等predict类型的replacement算法非常的不友好，因为图的遍历无论是出度遍历还是入度遍历，其下一个层都是未知，没有规律可循，也许某个vertex目前是高re-reference，但是后面的层几乎不会用到,但是图应用非常非常的适合

Belady’s MIN replacement(T-OPT)

接着上面的讲首先,我们普通的cache替换算法不能满足图应用场景，因为在图应用下，我们深度优先遍历完全不知道下一层的情况，可能下一层(按照出度)有4个子节点，其中有的节点是上一次访问的节点，有的是新的节点等等情况，所以图应用情况下我们传统的替换算法比如LRU，比如SHiP很难做到有效的predict。

图应用基本知识

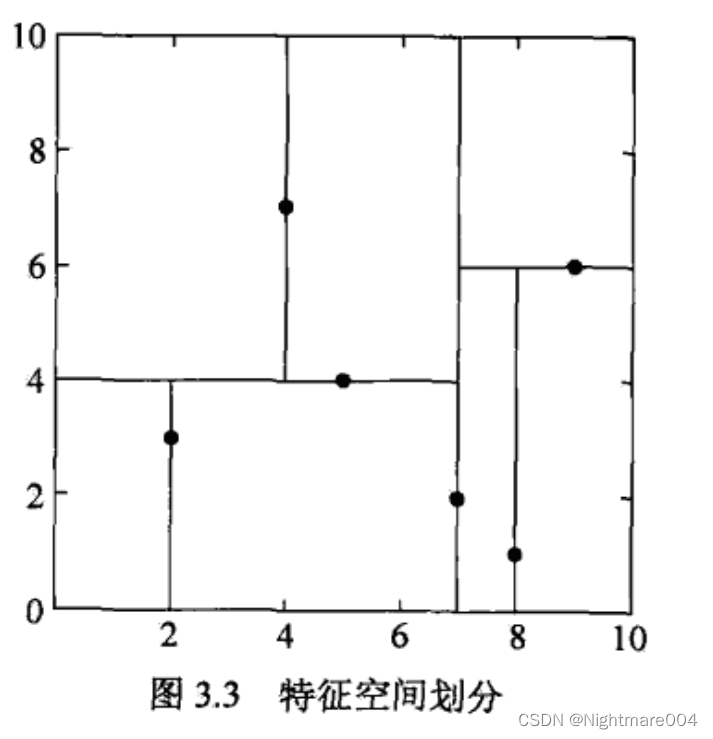
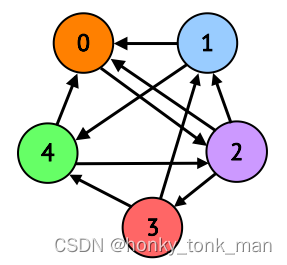
在我们要高效的为图应用开发缓存替换算法，知晓那个vertex下一次会被重用，我们先要了解图的结构，如下我们有一个图

上述的图是用markdown的mermaid画的，有些难看，也可以看下面这个图一样的内容

在计算机种如何表示存储他们呢？学过数据结构的图论我们知道用邻接矩阵(adjacency matrix)表示,如下图
$$\left[\begin{array}{ccccc}0& 0& 1& 0& 0\\ 1& 0& 0& 0& 1\\ 1& 1& 0& 1& 0\\ 0& 1& 0& 0& 1\\ 1& 0& 1& 0& 0\end{array}\right]$$
raw代表Src目的vertex，col代表Dst的Vertex，什么意思呢，从S0到D0也就是第0行第0列为0代表从vertex 0 到vertex0没有连接的线，从S0到D2为1(第0行，第2列)为1，说明从vertex 0到vertex2有连接的线，依此类推

换个形式矩阵如下

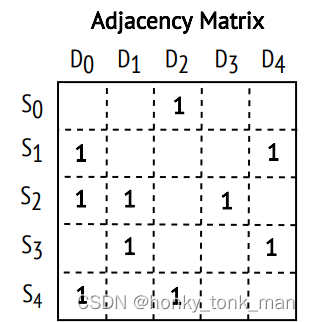
S0代表以0为起点进行遍历，S0->D0为0代表，S0到D0之间没有相连，S0->D2代表以0为起点到2(2为终点)有线相连

CSR和CSC

通过上一节我们知道图是如何在计算机存储，与此同时大家有没有想到过一个问题，假如我们的vertex(顶点)非常的多，不再是上一节描述的5个，而是十万个，那么我们为其创建的邻接矩阵大小为十万乘以十万,那么我们的邻接矩阵大小有10,000,000,000个元素，假设一个元素存储一个int大小的字符，再假设在普通的x86-64平台上int大小4个字节，为了存储这个图我们需要花费40,000,000,000字节大小，也就是40G大小的内存(这里用1M=1000Byte估算)，假设我们的顶点再多下去一个图占用的内存容量不敢想
通过观察上节图对应的邻接矩阵发现，其中大部分都是0，0代表2个vertex之间没有互连，我们能不能将其压缩，减少图在计算机中存储的空间?此时最广为流行的2种压缩方法，CSR和CSC诞生
CSR(Compressed Sparse Row)
从名字中可以看出是对行进行压缩，具体如何压缩还是上节的图为例子，CSR(CSC)分为2个部分，分别是OA(offset)数组和NA(number)数组,OA是一行一行遍历，从0开始一个1(代表顶点互联)才算一个,CSR的OA数组只记录每行第一个元素偏移量，且OA是NA数组中的偏移量，NA代表顶点，看例子

$$\left[\begin{array}{ccccc}0& 0& 1& 0& 0\\ 1& 0& 0& 0& 1\\ 1& 1& 0& 1& 0\\ 0& 1& 0& 0& 1\\ 1& 0& 1& 0& 0\end{array}\right]$$
我们进行CSR压缩后为2个数组

OA---> 0,1,3,6,8
NA--->2,0,4,0,1,3,1,4,0,2

首先OA中0代表第一个偏移量也就是第0行第2列的元素(第0行遍历开头的元素)
OA第二个元素是1代表第1行第0列的元素(第1行开头的元素，因为他也是矩阵中第2个元素，所以他的偏移量为1)
此时根据前2个偏移量我们可以定位邻接矩阵的第0行元素也就是2(记住OA是NA的偏移量0代表第0行起使，1带代表第一行的起使元素)，以此类推

Compressed Sparse Column
从名字中可以看出是对列进行压缩，我们后面的例子都会用到CSC，CSC是通过列为顺序进行遍历，还是上述的图，上述的邻接矩阵他的OA和NA如下图

OA ---> 0,3,5,7,8
NA ---> 1,2,4,2,3,0,4,2,1,3

OA第一个元素0和第二个元素3代表第一列的vertex1，2，4(0代表第0列的首偏移量，3代表第一列的首偏移量)

然后我们的图遍历算法就非常好解释，如下伪代码

for dst in G do
	for src in G.in_neighs(dst) do
		dstData[dst] += srcData[src]

先找到一个终点,然后不断地去遍历其入度，dstData和srcData内容相同都是顶点的集合

T-OPT替换算法使用

关于T-OPT和P-OPT的介绍来源于论文Balaji, Vignesh, et al. “P-opt: Practical optimal cache replacement for graph analytics.” 2021 IEEE International Symposium on High-Performance Computer Architecture (HPCA). IEEE, 2021.

T-OP算法的思想非常简单，在我们遍历的时候比如一列一列的遍历，先以D0为终点(顶点0为终点)，遍历其入度，也就是一列，在遍历到S0的时候会对S0这一行进行遍历，寻找下一次的reuse是什么时候(在什么vertex为终点的时候S0会被rereference)
还是相同的例子

CSC:
OA ---> 0,3,5,7,8
NA ---> 1,2,4,2,3,0,4,2,1,3

我们先是以D0为终点进行0的入度遍历，遍历第0列，遍历到S0的时候，我们会遍历上述的S0的这一行(如何实现根据CSR直接遍历)发现在顶点为2的时候，S0会被再次rereference，这个时候我们将这个消息记录下来，当Cache不够准备替换S0这个数的时候作为参考是否替换S0，然后以此类推

T-TOP非常的简单，但是有一个严重的问题，就是我们在进行横向遍历的时候(比如上述例子第一行横向遍历找到S0在什么时候会被rereference)，时间复杂度是O(n)，假设顶点非常非常的多，我们T-TOP算法的效率也会随之急剧下降，T-TOP的理想情况是将这种遍历带来的时间成本给抹掉，当然这不可能，所以为了解决这个隐患，人们又开发了一个叫做P-OPT的算法，P-OPT是T-OPT的改进

P-OPT

和上一节说的一样P-OPT是为了适应T-OPT在实际使用中为了预测vertex下一次什么时候被reuse，而遍历整个row，P-OPT采用了2种矩阵去解决此问题，分别是Rereference Matrix(RM)和Modified Rereference Matrix(MRM),其中MRM是RM的改进版本，因为在RM还是不够高效

Rereference Matrix

我们在使用P-OPT的时候会专门为图生成一个矩阵(Rereference Matrix或者Modified Rereference Matrix)，这个矩阵没有邻接矩阵大，我们首先介绍的版P-OPT V1使用的是Rereference Matrix，其具体如下，我们会先给邻接矩阵分为多个epoch,epoch可以看成分组,一个epoch由多个colum组成，还是上述的例子，图和邻接矩阵如下

我们将D0和D1放入epoch1，D2和D3放入epoch2，D4单独放入epoch3，然后我们生成Rereference Matrix，矩阵如下
$$\left[\begin{array}{c}S0\\ S1\\ S2\\ S3\\ S4\end{array}\right]\left[\begin{array}{ccc}1& 0& m\\ 0& 1& 0\\ 0& 0& m\\ 0& 1& 0\\ 0& 0& m\end{array}\right]$$

上述的矩阵可能画的有一些抽象，具体想表达的意思是S0这个源Vertex对应的是1,0,m，S1这个源Vertex对应的是0,1,0，然后Rereference Matrix的三个列分别对应epoch1，epoch2，epoch3，最值得注意的是每一个row都存于不同的cache line中

如上述的Rereference Matrix每一个colum都是一个epoch，其代表当前的epoch到下一次(下一个epoch)被reuse的距离，比如上述S0，在epoch1中(D0和D1)不会被reuse，并且他们会在epoch2(D2和D3中的D2)中被reuse，所以在Rereference Matrix中S0对应的row中，第一个元素应该是1代表下一个epoch才会被reuse(下次reuse的距离为1)，当我们loop到epoch2(D2和D3)的时候对应的元素(S0对应的row第二个元素)为0，代表这个epoch会被reuse，当我们loop到epoch3(D4)的时候S0对应的是m，代表本epoch内不会被reuse，且后续也不会被reuse

上述的Rereference Matrix大大的降低了我们P-OPT在进行predict的时候遍历的操作，但是Rereference Matrix有一个极其严重的问题，当我们的epoch大小越来越大(D0,D1…数量)，我们Rereference Matrix对应的元素为0代表在次epoch中会被reuse，但是我们不知道具体在哪里reuse，也有可能已经reuse了可以将对应的S0或者S1等等对应的vertex临时替换出去，但是在Rereference Matrix中并不会，换句话说我们的Rereference Matrix颗粒度还是过于大，所以有了更新的Rereference Matrix叫做Modified Rereference Matrix

Modified Rereference Matrix

还记得我们之前说Rereference Matrix的每一个row都缓存于每一个cache line中，在Modified Rereference Matrix(MRM)中每个元素由2个term组成分别是

• MSB(most significant bit)：1个bit用于记录当前的epoch是否会被reuse
• inter/intra epoch info：7bit，用于记录下次reuse到现epoch的距离

我们直接上具体的算法进行讲解，该算法用Rereference Matrix寻找下一个reference

1: procedure FINDNEXTREF(clineID,currDstID)
2: 	epochID ← currDstID/epochSize
3: 	currEntry ← rerefMatrix[clineID][epochID]
4: 	nextEntry ← rerefMatrix[clineID][epochID+1]
5: 	if currEntry[7] == 1 then
6: 		return currEntry[6 : 0]
7: 	else
8: 		lastSubEpoch ← currEntry[6 : 0]
9: 		epochStart ← epochID ∗ epochSize
10: 	epochOffset ← currDstID−epochStart
11: 	currSubEpoch ← epochOffset/subEpochSize
12: 	if currSubEpoch ≤ lastSubEpoch then
13: 		return 0
14: 	else
15: 		if nextEntry[7] == 1 then
16: 			return 1 + nextEntry[6:0]
17: 		else
18: 			return 1

首先有必要解释一下epochSize代表的是epoch内部D0,D1…之类colum的数量，rerefMatrix就是我们的Rereference Matrix一个二维数组，clineID就是我们的Cache Line ID，因为我们提到一个cache line存储一个row，在这里Rereference Matrix每一个元素分为MSB和inter/intra epoch info，一共占用8个bit，currEntry代表Rereference Matrix中的某个元素，然后我们分析代码
首先我们要确定当前所处的epoch的id，如图上所示第二行代码，currDstID就是我们的D0,D1…这类的ID，然后取出对应的当前Rereference Matrix元素，和下一次reuse的元素(分别4-5行代码)，然后判断当前的entry的MSB是否置为1，假如置为1那么代表当前的epoch没有reuse，那么直接返回下entry中的inter/intra epoch info告诉函数调用者什么时候会被reuse(第六行代码)，假如当前entry的MSB置为0说明当前的epoch会被reuse，此时我们要避免之前的情况发生，这里要判断当前epoch中是否已经reuse了还是没有reuse，在这里定义了一个subepoch的概念为的就是将颗粒度变细(个人觉得没有本质解决问题)，然后找出当前epoch中下一次reuse的subepoch和当前所在的subepoch进行比较，假如还没到或者正处于下一次reuse的subepoch就返回0代表最不可能被cache替换算法替换出去(代码12-13行),假如已经超过判断下一个matrix entry是否会reuse次vertex，如果不会reuse，那么就返回1+下一次什么时候会被reuse(15到16行，+1代表当前到下一个entry的路径)，如果下一次会被reuse(代码17行)就返回1优先级仅次于0

这个就是算法的全部解释