【机器学习】决策树如何实现回归

1. 介绍

在 https://blog.csdn.net/qq_51392112/article/details 中，我们详细介绍了决策树基本内容：如何实现、决策树的类型、公式计算等，内容更偏向于决策树的分类任务，而分类任务也是很好理解的，因为直观上来说，决策树本身就很适合分类任务。

• 但是决策树还可以实现回归任务，这一讲我们将要细讲。
• 与线性回归不同，回归树是将“空间”进行划分，每个空间则对应一个统一的预测值。

2. 回归树的构建方法

1）预测的标签值是根据该区域（空间）内的总样本数平均化得出的。

2）与线性回归类似，回归树也需要一个损失函数对回归的效果进行评估，这里采用平方残差和RSS进行评估：

• 其中，$y_i$ 是样本的真实值，$y_{R_j}$ 是第 $R_j$ 空间所有样本的预测值。
• 内层 ∑ 就是将该区域内所有的样本预测值和真实值的差值平方进行加和；
• 外层 ∑ 就是遍历所有划分出来的区域。

但是如果我们仔细想一下，如果采用这种方法来回归，这个计算量是惊人的，因为空间划分有太多的情况，为了处理这种问题，我们常使用一种方法对划分空间提出了简化要求！

• 这种方法称作“递归二分法”！

3. 递归二分法

什么是递归二分？顾名思义，树的每次分裂都以二叉树的形式分裂。当我们初步根据特征及其最佳划分点分裂出了2个子结点（即空间）RJ
​后，不断从当前位置，继续将该空间的样本再次划分成2份！

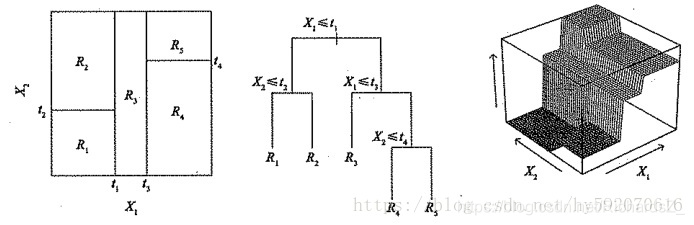
1）划分方案：

• 自顶向下，从所有样本开始，不断从当前位置，把样本切分到2个分支里
• 贪婪，每一次的划分，只考虑当下划分的最优，不回头考虑先前的划分

2）优化原则：

• 选择切分的维度x_j （即将数据的每一个特征）以及切分点s，使得再次划分后的回归树RSS结果最小
  

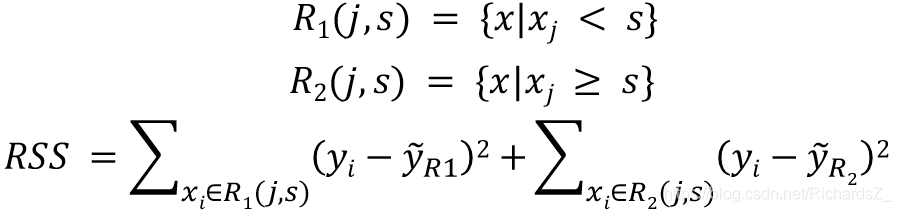
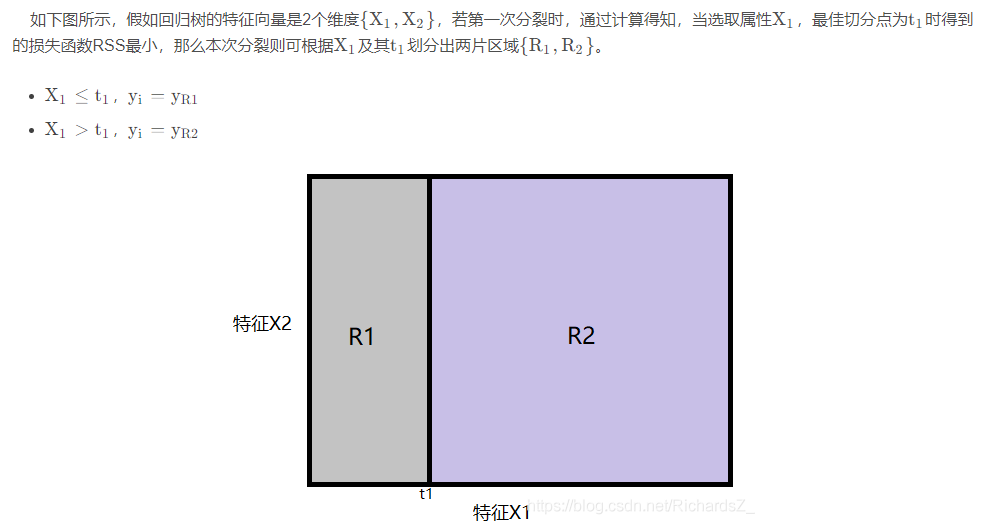
通俗来说，当我们初步划分出了两个空间后，接下来，将继续根据损失函数RSS开始选择维度，以及该维度下的切分点 t 再次将 子空间进行二分。

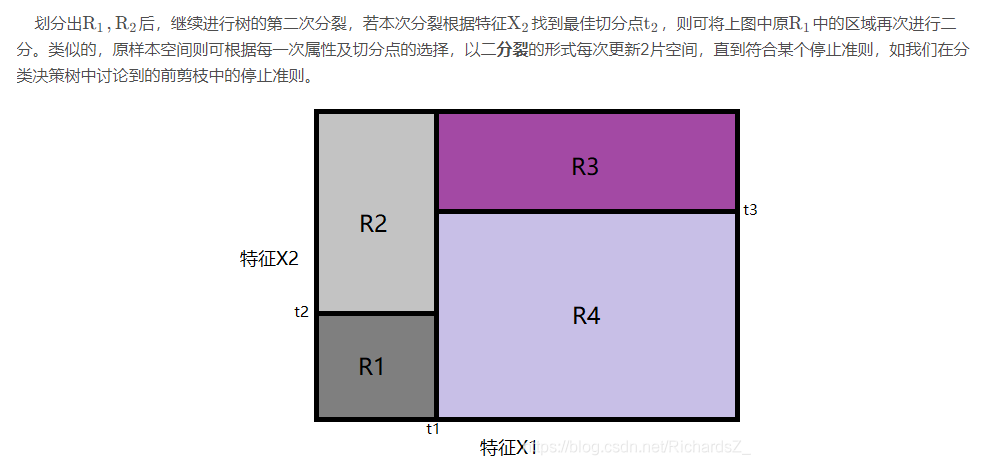
4. 回归树的剪枝

同样的，回归优化的过程同线性回归一样，在通过降低损失函数来优化模型的过程中，模型容易陷入“过拟合”的状态。同样需要引入“正则化项”作为惩罚。

• 与线性回归区别的是，由于回归树并不是数值模型，所以正则化项不可以引入如L2正则化项这种数值项，因此回归树里的正则化项与叶子结点相关：
  
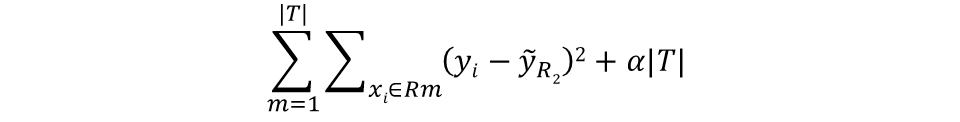
  这里的 ∣T∣示树T的结点数，当超参数α > 0时，树的结点越多，代表模型越复杂，树将为它的复杂性付出代价，所以使上式取到最小值的子树会变得更小。

5. 总结

回归决策树算法：

1. 利用递归二叉分裂在训练集中生成一棵大树，只有当终端结点包含的观测值个数低于某个最小值时才停止。
2. 对大树进行代价复杂性剪枝，得到一系列最优子树，子树是 α 的函数。
3. 利用K折交叉验诞选择 α 。具体做法是将训练集分为K折。
   • 对所有k = 1 , 2 , 3 , ⋯ K; 对训练集上所有不属于第k折的数据重复第(1)步~第(2)步得到与α对应的子树，并求出上述子树在第k折上的均方预测误差。
4. 每个α会有相应的K个均方预测误差，对这K个值求平均，选出使平均误差最小的α。
5. 找出选定的α在第(2)步中对应的子树。

参考

【1】https://blog.csdn.net/RichardsZ_/article/details/108903858