提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 1 算法原理
- 2 算法步骤
- 2.1 初始化种群
- 2.2 搜索猎物(全局搜索)
- 2.3 包围和围捕猎物(局部搜索)
- 2.4 从全局搜索转向局部搜索
- 3 算法流程图
- 4 matlab代码实现
- 运行F3测试案例
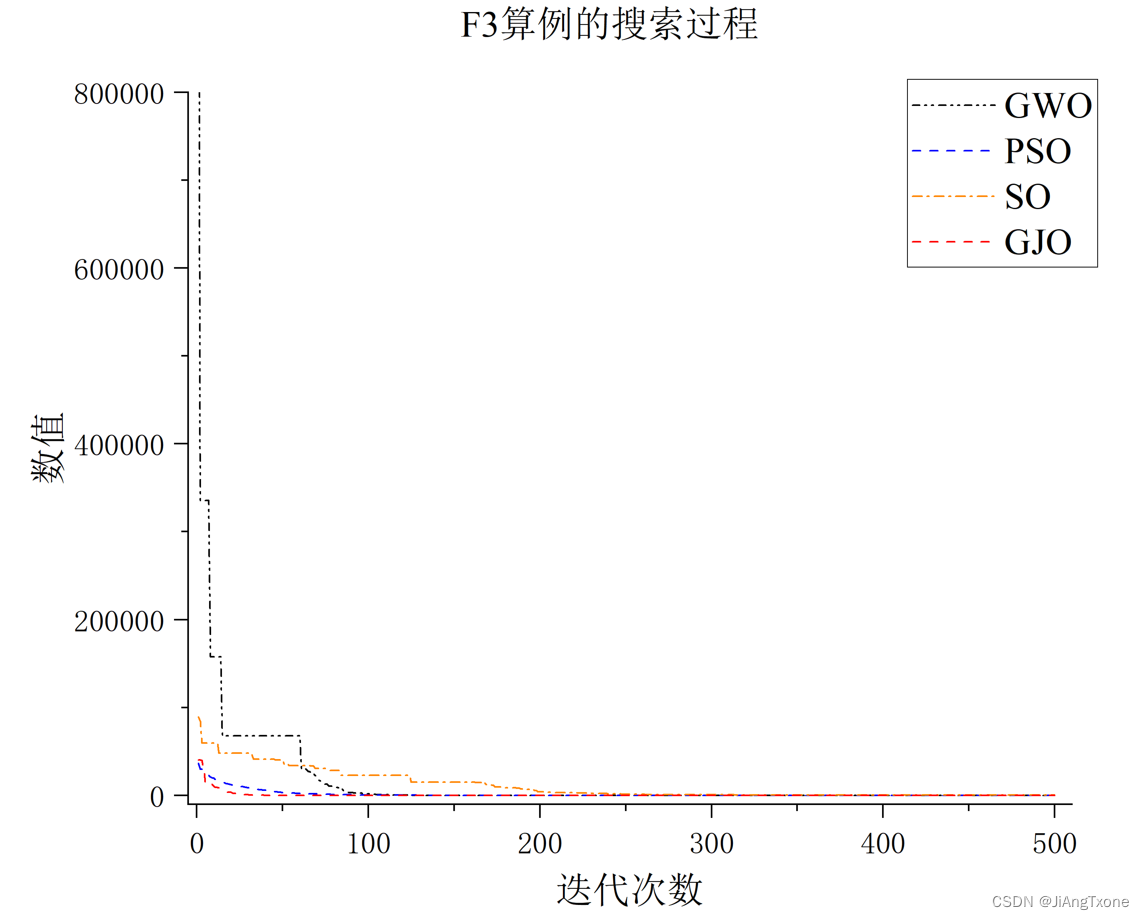
- 与GWO、PSO、SO算法进行比对——F3算法
前言
金豺(GJO)优化算法是2022年由Nitish Chopra 等人提出,GJO 的灵感来自金豺 (Canis aureus) 的协作狩猎行为。算法的三个基本步骤是猎物搜索、包围和突袭 。
1 算法原理
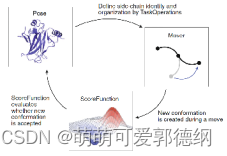
该算法主要是由雄雌豺狼带领各个豺狼对猎物进行搜索、包围和围捕。
A:雄雌豺狼对
B:个体搜索猎物
C:包围猎物
D&E:围捕猎物

2 算法步骤
2.1 初始化种群
对个体进行初始化,和大部分算法一样,Ymax:表示上界,Ymin:表示下界
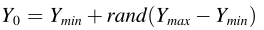
通过上述公式对种群进行初始化。
2.2 搜索猎物(全局搜索)
Ym(t):所有豺狼个体中最好的个体——雄性豺狼
Yfm(t):所有豺狼个体中次好的个体——雌性豺狼
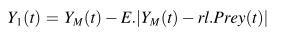
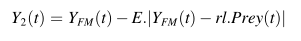
E的计算公式:
E:回避能量
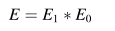
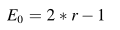
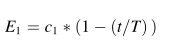
c1=1.5,E1为从1.5~0线性递减。
rl的计算公式:
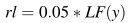
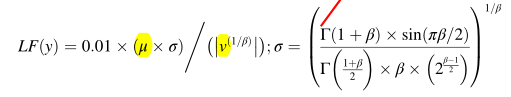
miu,v 为0-1的随机数,beta=1.5;
ps:τ对应matlab函数中的gamma函数。
豺狼个体更新位置的公式:
ps:有点类似于灰狼优化算法个体更新位置的公式
算法的探索阶段(全局搜索)使用如下3个公式对豺狼个体进行位置更新。
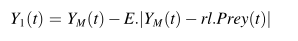
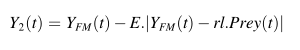
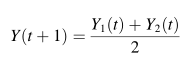
2.3 包围和围捕猎物(局部搜索)
算法的开发阶段(局部搜索)使用如下3个公式对豺狼个体进行位置更新
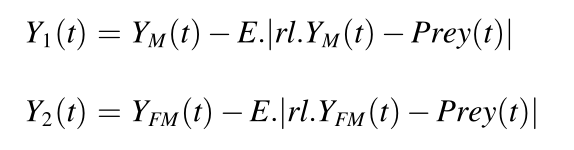
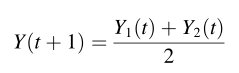
2.4 从全局搜索转向局部搜索
主要通过躲避能量的绝对值大小进行改变
当|E|>=1,豺狼对不同部分探索猎物,
当|E|<1,豺狼开始包围和攻击猎物。
3 算法流程图
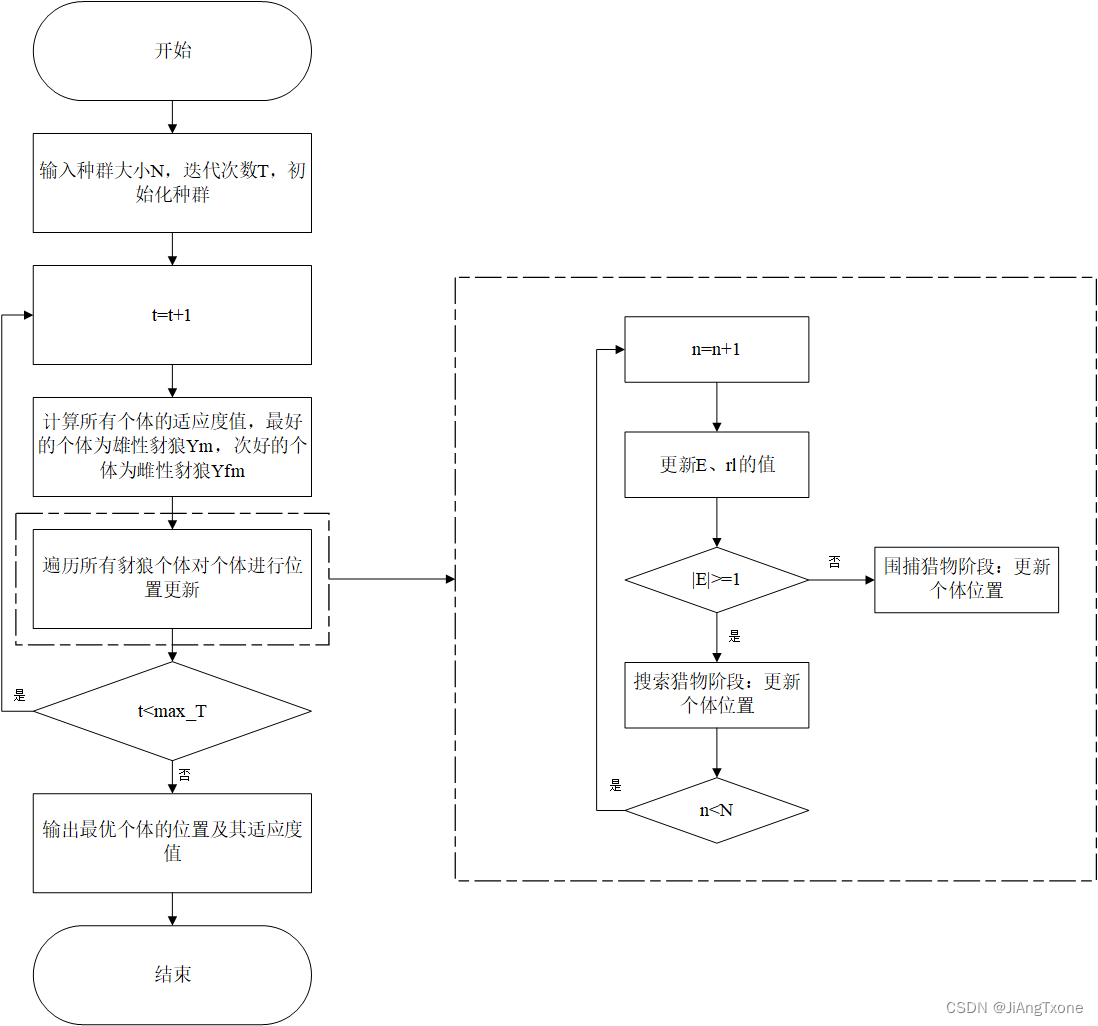
4 matlab代码实现
main函数:
close all;
clear all;
clc;
% N种群大小
% Dim个体维度
% T最大迭代次数
% ub上界
% lb下界
% X_prey最好的个体
% G_best存储每次迭代后的最好个体的适应度值
N=300;
Dim=30;
T=500;
ub=100;
lb=-100;
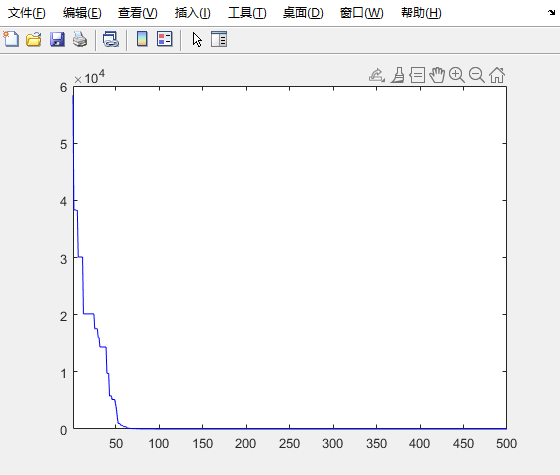
[Y_prey,G_best]=GJO(Dim,ub,lb,N,T);
figure,
plot(G_best,'Color','blue');
best=G_best';%转置用于origin填充数据使用
xlim([1,500]);
my_function函数:
function my_fitness=my_function(X)
%F3测试问题
dim=size(X,2);
o=0;
for i=1:dim
o=o+sum(X(1:i))^2;
end
my_fitness=o;
end
GJO主体代码
function [Y_prey,G_best]=GJO(Dim,ub,lb,N,T)
%% 初始化参数
c1=1.5;
beta=1.5;
%% 初始化种群
Pop=zeros(N,Dim);
Pop_size=size(Pop,1);
for i=1:Pop_size
for j=1:Dim
Pop(i,j)=lb+rand*(ub-lb);
end
end
%% 进化
for t=1:T
%筛选雄雌豺狼个体
for i=1:Pop_size
fit_ness(i)=my_function(Pop(i,:));
end
[~,sort_index]=sort(fit_ness);
Y1=Pop(sort_index(1),:);%雄性豺狼
Y2=Pop(sort_index(2),:);%雌性豺狼
Y1_fitness=fit_ness(sort_index(1));%雄性豺狼适应度值
Y2_fitness=fit_ness(sort_index(2));%雌性豺狼适应度值
for i=1:Pop_size
for j=1:Dim
%eq(6)~eq(8)
E0=2*rand-1;
E1=c1*(1-(t/T));
E=E1*E0;
%eq(9)~eq(10)
miu=rand;
v=rand;
sita=((gamma(1+beta)*sin(pi*beta/2))/(gamma((1+beta)/2)*beta*2.^((beta-1)/2))).^(1/beta);
LF=0.01*(miu*sita)/(abs(v.^(1/beta)));
rl=0.05*LF;
if abs(E)>=1
Y1_new=Y1(j)-E.*abs(Y1(j)-rl.*Pop(i,j));
Y2_new=Y2(j)-E.*abs(Y2(j)-rl.*Pop(i,j));
Y_new(i,j)=(Y1_new+Y2_new)./2;%紧随雄雌豺狼,更新豺狼位置 eq(4)、(5)and(11)
else
Y1_new=Y1(j)-E.*abs(rl*Y1(j)-Pop(i,j));
Y2_new=Y2(j)-E.*abs(rl*Y2(j)-Pop(i,j));
Y_new(i,j)=(Y1_new+Y2_new)./2;%紧随雄雌豺狼,更新豺狼位置 eq(12)、(13)and(11)
end
end
end
%% 计算所有新更新个体的适应度值
for i=1:Pop_size
Flag4Up=Y_new(i,:)>ub;
Flag4Lp=Y_new(i,:)<lb;
Y_new(i,:)=(Y_new(i,:).*(~(Flag4Up+Flag4Lp)))+Flag4Up.*ub+Flag4Lp.*lb;%修正
y=my_function(Y_new(i,:));
if y<my_function(Pop(i,:))
fit_ness(i)=y;
Pop(i,:)=Y_new(i,:);%替换个体
end
end
%% 更新雄雌豺狼
[~,sort_index]=sort(fit_ness);
Y1=Pop(sort_index(1),:);%雄性豺狼
Y2=Pop(sort_index(2),:);%雌性豺狼
Y_prey=Y1;%最好的个体
G_best(t)=my_function(Y1);%每次迭代后计算雄性豺狼个体的适应度值
end
end
运行F3测试案例
与GWO、PSO、SO算法进行比对——F3算法