目录
- 前言
- 实验目的
- 实验内容
- 实验过程
- 最佳置换算法
- 代码实现
- 算法流程
- 流程图
- 设计思路
- 运行结果
- 先进先出算法
- 代码实现
- 算法流程
- 流程图
- 设计思路
- 运行结果
- 最近最久未使用算法
- 代码实现
- 算法流程
- 流程图
- 设计思路
- 运行结果
- 总结
前言
本实验的目的是通过编程模拟不同的页面置换算法,比较它们的缺页率和命中率,加深对操作系统内存管理的理解。本实验采用C语言编写,实现了最佳置换算法(OPT)、先进先出置换算法(FIFO)和最近最久未使用算法(LRU)。实验中,页面号引用串从文本文件中读取,输出每次访问页面时内存中的页面情况,以及最终的缺页次数、缺页率和命中率。本文档将介绍实验的设计思路、流程图、代码和运行结果。
实验目的
(1)理解虚拟存储器的内存分页管理策略,掌握请求调度与置换的工作过程。
(2)掌握常用页面置换算法的思想,编制程序,将调试结果显示在计算机屏幕上,并检测机算和笔算的一致性。
(3)了解页面大小和内存实际容量对命中率的影响。
实验内容
(1)编程实现最佳置换算法(OPT)算法
(2)编程实现先进先出(FIFO)算法
(3)编程实现最近最久未使用(LRU)算法
基本要求:
(1)任选以上两种算法进行实现。
(2)能够根据给定的引用串及物理块数,在屏幕上输出该算法对应的置换图,及其缺页次数和缺页率。
实验过程
最佳置换算法
最佳置换算法(Optimal Page Replacement Algorithm)是一种理论上的页面置换算法,它通过选择以后不再使用或者在最长时间内不再被访问的页面进行置换,从而达到最低的缺页率。
最佳置换算法根据本人的理解是一种理想中的算法,它通过预测未来将会访问的页面进行页面置换,无疑,这将会最大程度的利用好资源,毕竟我们都已经知道未来会发生的事情,那自然可以做出 最好的选择,可惜世界又怎么会事事如意呢,因此,至少在目前,仍然只是一种理想中的算法罢了。
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
int findOptimal(int pages[], int n, int index, int frame[], int f) {
int res = -1;
int farthest = index;
for (int i = 0; i < f; i++) {
int j;
for (j = index; j < n; j++) {
if (frame[i] == pages[j]) {
if (j > farthest) {
farthest = j;
res = i;
}
break;
}
}
if (j == n)
return i;
}
return (res == -1) ? 0 : res;
}
void optimalPage(int pages[], int n, int f) {
int frame[f];
for (int i = 0; i < f; i++)
frame[i] = -1;
int hit = 0;
for (int i = 0; i < n; i++) {
int j;
for (j = 0; j < f; j++)
if (frame[j] == pages[i]) {
hit++;
break;
}
if (j == f) {
int l = findOptimal(pages, n, i + 1, frame, f);
frame[l] = pages[i];
}
printf("\n");
for (int k = 0; k < f; k++)
printf("%d ", frame[k]);
}
printf("\n\n缺页次数: %d", n - hit);
printf("\n缺页率: %f\n", (n - hit) / (double)n);
}
int main() {
int pages[] = {7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3};
int n = sizeof(pages) / sizeof(pages[0]);
int f = 4;
optimalPage(pages, n, f);
return 0;
}
算法流程
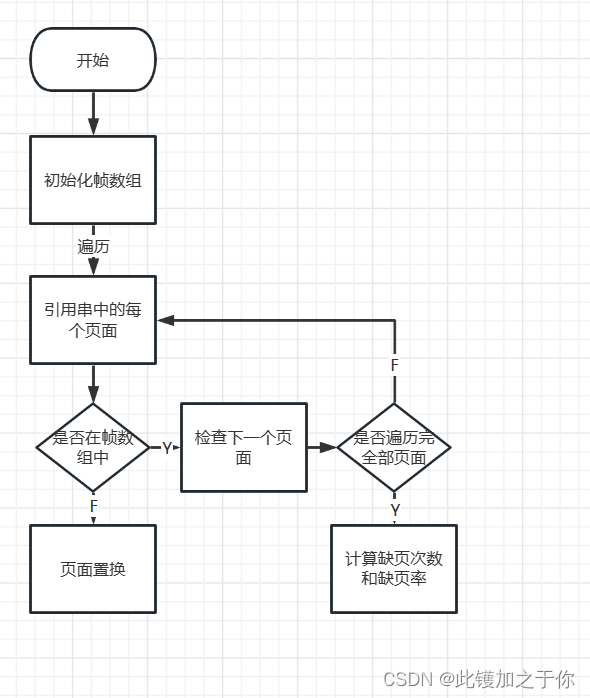
- 初始化一个大小为物理块数的帧数组,用于存储当前在内存中的页面。
- 遍历给定的引用串中的每个页面。
- 对于每个页面,检查它是否已经在帧数组中。如果是,则跳过该页面并继续遍历下一个页面。
- 如果该页面不在帧数组中,则需要进行页面置换。找到帧数组中以后不再使用或者在最长时间内不再被访问的页面,并用当前页面替换它。
- 重复步骤3和4,直到遍历完引用串中的所有页面。
- 计算缺页次数和缺页率。
流程图
设计思路
思路是通过选择以后不再使用或者在最长时间内不再被访问的页面进行置换,从而达到最低的缺页率,最佳置换算法是一种理论上的算法,因为它需要预先知道引用串中每个页面将来会被访问的时间,这在实际应用中是不可能做到的。但是,它可以作为其他页面置换算法的性能评估标准。
运行结果

上面的输出显示了最佳置换算法在每个时刻的帧数组状态,以及最终的缺页次数和缺页率。使用了一个引用串 {7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3} 和物理块数 4 来演示最佳置换算法。
先进先出算法
先进先出算法是一种简单的页面置换算法,它通过选择最早进入内存的页面进行置换,从而达到页面置换的目的。
一种比较朴素的思想
代码实现
#include <stdio.h>
#include <stdbool.h>
void fifoPage(int pages[], int n, int f) {
int frame[f];
for (int i = 0; i < f; i++)
frame[i] = -1;
int hit = 0;
int pointer = 0;
for (int i = 0; i < n; i++) {
bool allocated = false;
for (int j = 0; j < f; j++)
if (frame[j] == pages[i]) {
hit++;
allocated = true;
break;
}
if (!allocated) {
frame[pointer] = pages[i];
pointer = (pointer + 1) % f;
}
printf("\n");
for (int k = 0; k < f; k++)
printf("%d ", frame[k]);
}
printf("\n\n缺页次数: %d", n - hit);
printf("\n缺页率: %f\n", (n - hit) / (double)n);
}
int main() {
int pages[] = {7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3};
int n = sizeof(pages) / sizeof(pages[0]);
int f = 4;
fifoPage(pages, n, f);
return 0;
}
算法流程
- 初始化一个大小为物理块数的帧数组,用于存储当前在内存中的页面。
- 遍历给定的引用串中的每个页面。
- 对于每个页面,检查它是否已经在帧数组中。如果是,则跳过该页面并继续遍历下一个页面。
- 如果该页面不在帧数组中,则需要进行页面置换。选择最早进入内存的页面进行置换,并用当前页面替换它。
- 重复步骤3和4,直到遍历完引用串中的所有页面。
- 计算缺页次数和缺页率。
流程图
流程图相同,但是页面置换有区别,在置换时选择最早进入内存的页面进行置换。
设计思路
思路是通过选择最早进入内存的页面进行置换,从而达到页面置换的目的,先进先出算法是一种简单且容易实现的页面置换算法,但它并不能保证获得最低的缺页率。在某些情况下,它甚至会导致比其他算法更高的缺页率。
运行结果

上面的输出显示了先进先出算法在每个时刻的帧数组状态,以及最终的缺页次数和缺页率。,它使用了一个引用串 {7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3} 和物理块数 4 来演示先进先出(FIFO)算法。
最近最久未使用算法
最近最久未使用算法是一种常用的页面置换算法,它通过选择最近最久未被访问的页面进行置换,从而达到页面置换的目的。
代码实现
#include <stdio.h>
#include <stdbool.h>
int findLRU(int time[], int f) {
int min = time[0];
int res = 0;
for (int i = 1; i < f; i++) {
if (time[i] < min) {
min = time[i];
res = i;
}
}
return res;
}
void lruPage(int pages[], int n, int f) {
int frame[f];
for (int i = 0; i < f; i++)
frame[i] = -1;
int time[f];
for (int i = 0; i < f; i++)
time[i] = 0;
int hit = 0;
for (int i = 0; i < n; i++) {
bool allocated = false;
for (int j = 0; j < f; j++)
if (frame[j] == pages[i]) {
hit++;
time[j] = i + 1;
allocated = true;
break;
}
if (!allocated) {
int lru = findLRU(time, f);
frame[lru] = pages[i];
time[lru] = i + 1;
}
printf("\n");
for (int k = 0; k < f; k++)
printf("%d ", frame[k]);
}
printf("\n\n缺页次数: %d", n - hit);
printf("\n缺页率: %f\n", (n - hit) / (double)n);
}
int main() {
int pages[] = {7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3};
int n = sizeof(pages) / sizeof(pages[0]);
int f = 4;
lruPage(pages, n, f);
return 0;
}
算法流程
- 初始化一个大小为物理块数的帧数组,用于存储当前在内存中的页面。
- 初始化一个大小为物理块数的时间数组,用于记录每个页面最近被访问的时间。
- 遍历给定的引用串中的每个页面。
- 对于每个页面,检查它是否已经在帧数组中。如果是,则更新该页面在时间数组中对应的值,并跳过该页面继续遍历下一个页面。
- 如果该页面不在帧数组中,则需要进行页面置换。选择时间数组中值最小的页面进行置换,并用当前页面替换它,同时更新该页面在时间数组中对应的值。
- 重复步骤4和5,直到遍历完引用串中的所有页面。
- 计算缺页次数和缺页率。
流程图
多初始化一个时间数组,用于记录每个页面最近被访问的时间,在置换时选择时间数组中值最小的页面进行置换,同时更新该页面在时间数组中对应的值。
设计思路
设计思路是通过选择最近最久未被访问的页面进行置换,从而达到页面置换的目的。最近最久未使用算法是一种常用且有效的页面置换算法,它能够在很多情况下获得较低的缺页率。但是,它需要额外的空间来存储每个页面最近被访问的时间,并且在每次访问时都需要更新时间数组,这会增加算法的时间复杂度。
运行结果

上面的输出显示了最近最久未使用算法在每个时刻的帧数组状态,以及最终的缺页次数和缺页率,它使用了一个引用串 {7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3} 和物理块数 4 来演示最近最久未使用(LRU)算法。
总结
本文总结了计算机操作系统实验中的三种页面置换算法:最佳置换算法(OPT)、先进先出置换算法(FIFO)和最近最久未使用置换算法(LRU)。页面置换算法是在内存已满且需要访问的页面不在内存中时,选择一个内存中的页面换出的方法。不同的算法有不同的选择标准和效率。最佳置换算法是选择在未来最长时间内不再被访问的页面换出,它可以保证最低的缺页率和置换率,但是它是无法实现的,因为我们无法预知未来的页面访问情况。先进先出置换算法是选择最先进入内存的页面换出,它实现简单,但是效率不高,可能会导致经常被访问的页面被频繁地换出。最近最久未使用置换算法是选择最久没有被访问的页面换出,它是根据过去的页面访问情况来预测未来的访问情况,但是这种预测并不一定准确,因此它的效率也不是很高。本文通过C语言编写程序,实现了这三种算法,并对它们进行了比较和分析。