回溯

本质上：穷举 + 剪枝。
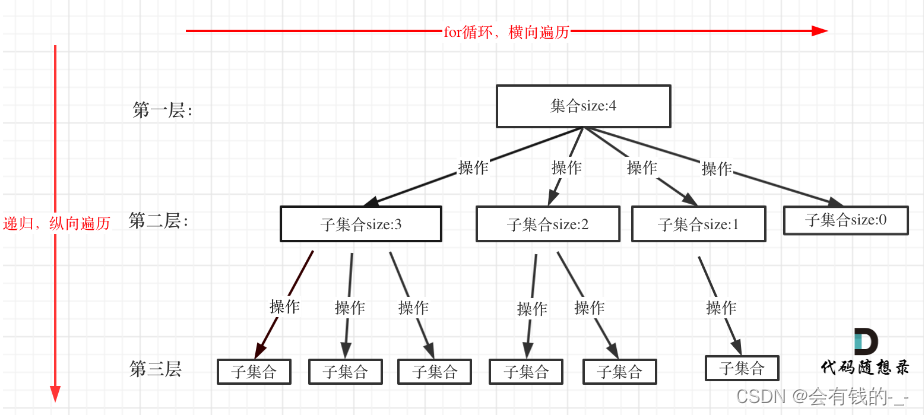
回溯法就是解决这种k层for循环嵌套的问题。
- for循环横向遍历，递归纵向遍历，回溯不断调整结果集。
注意画出解空间树-N叉树。

细节

组合无序，排列有序。
N叉树的宽度——横向遍历，N叉树的高度——纵向遍历。
- 而ans.push，path 是一个 std::vector 对象，当你将其传递给 push_back() 函数时，它会被以值传递的方式进行添加。也就是说，ans 容器会创建一个新的 std::vector 对象，这个新对象的元素值与 path 对象的元素值相同，但是它们位于不同的内存位置上。因此，这不是引用传递。
集合常用排序先进行预处理

模板

请添加图片描述

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

题型

组合

N个数里面按一定规则找出k个数的集合。

细节
- 需要保存N叉树所有符合的结果——叶子，定义path、ans，而将path加入ans的方法细节。
  - 在C++中，当使用 push_back() 函数将一个元素添加到 std::vector 容器中时，如果该元素是一个对象，那么它可以通过值传递或者引用传递的方式进行添加。如果传递的是一个对象的引用，那么新元素就会引用这个对象。一般是直接传递对象，进行值传递，拷贝一个path。
剪枝
- 对N叉树的高度剪枝，在每次进入下一层递归前进行判断剪枝（或者在递归函数开始之前，相当于在模板的终止条件之前），记得回溯。
- 对N叉树的宽度剪枝，for循环的范围剪枝，剩余个数是否满足条件。
类型
- 单个集合、多个集合
  - 单个集合内的组合，用到beginIdx，当前元素从该集合哪开始。
  - 多个集合间的组合，用到index，当前元素从哪个集合得到。
- 组合没有数量要求
  - 没有组合数量要求，仅仅是总和的限制，所以递归没有层数的限制，只要选取的元素总和超过target，就返回。
- 元素可无限重复选取
  - 关键点:进入下一层递归不用i+1，表示可以重复读取当前的数。
- 去重——参照解空间树
  - 树枝去重
    - 同一种组合内不可以有重复元素，即一种树枝路径为一种组合结果。
  - 树层去重
    - 不同组合不允许相同
    - 一般都会利用 used数组和排序 辅助树层去重。
  - used数组
    在candidates[i] == candidates[i - 1]相同的情况下：
    - used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
    - used[i - 1] == false，说明同一树层candidates[i - 1]使用过
    - 该used数组也需要记得回溯。

分割

一个字符串按一定规则有几种切割方式。

细节
- 类似组合问题，抽象为N叉树。
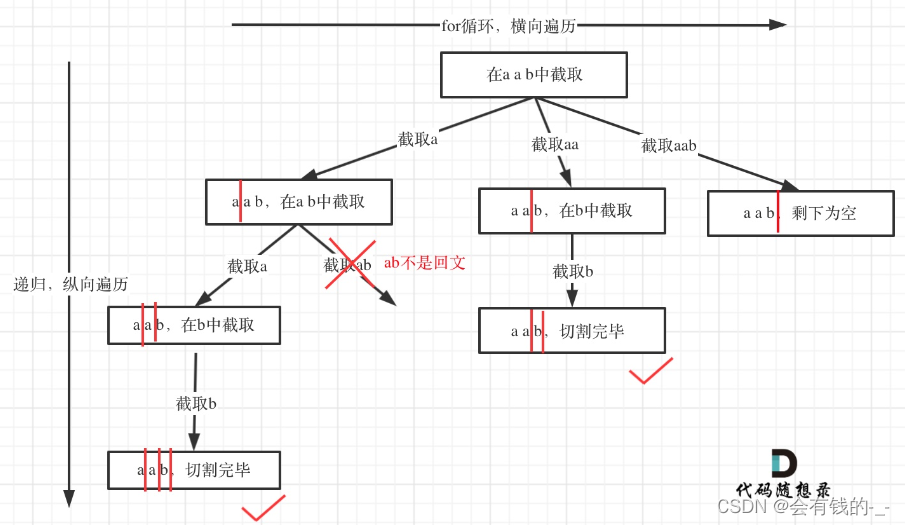
  - 理解横向遍历与纵向遍历。
- 切割线：用beginIdx模拟。
- 终止条件
  - 一种，当前方案已经切割到了最后，即beginIdx == end，可以直接加入path——解空间树一条路径。
  - 一种，在倒数第二位置时，最后一段已经确定了，只需要判断最后一段（叶子）是否合法，再决定是否加入该条路径path。
- 拼接vector<string>
```
    #include<numeric>
    ans.push_back(
        accumulate(path.begin(), path.end(), string{},
            [](const string& a, const string& b)->string {return a.empty() ? b : a + "." + b; })
    );
```

子集

一个N个数的集合里有多少符合条件的子集。

细节
- 遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合，可能根据条件对节点进行筛选。
- 求取子集问题，不需要任何剪枝！因为子集就是要遍历整棵树。
- 终止条件问题
  - 可以忽略终止条件，这是因为for从 beginIdx开始且下一层是i+1，for会到达size。
类型
- 取有序的子集的去重
  - 同一父节点下的同一层节点进行去重
    - 排序不可用。
    - 在每一层构建一个哈希集合，对当前层去重。
    - 若是元素值范围有限且较小，可直接使用数组，来进行哈希优化。
    - 当前层的哈希去重没有类似pop的操作。在当前层结束后，该层的去重哈希集合便销毁了。
    - 代码
```
// 
if ((used[nums[i] + 100] == 1))
    continue;
```

排列

N个数按一定规则全排列，有几种排列方式。

细节
- 排列问题，每次都要从头开始搜索。
  - 每层都是从0开始搜索，不使用beginIdx。
  - 使用used数组，其实就是记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次。
去重
- 类型
  - 树层去重
- 方法
  - 排序
  - used数组

棋盘问题

N皇后，解数独等等。

N皇后问题

细节
- 解空间树，最大高度即棋盘边长，宽度也是。
- 每一递归表示一层，对于棋盘中的一行，又由于回溯操作，所以在检查该棋子是否能放置时同行不需要检查。
- 终止条件：当前行==n，棋盘边长。

解数独问题

细节
- 不同于N皇后问题，数独问题，每一行的每一个空格都要填充数字，所以起始行永远=0。
- 终止条件：没有终止条件，全部填充即可，充分利用回溯函数的返回值bool。

其他

总结

1-解空间树节点
- 组合、分割、排列问题，求叶子节点——路径。
- 子集问题，求所有节点。
2-同一层遍历的起点
- 组合、分割、子集，属于无序，for从 beginIdx开始。
  - 组合问题中，若是2个集合内的组合，不需要 beginIdx。
- 排列，属于有序，for从 0开始。
3-去重
- 类型
  - 树枝去重
  - 树层去重
  - 同一父节点的同一层子节点之间去重
- 方法
  - 排序
  - used数组
  - 在该层使用哈希集，生命周期只在该层即本次递归中存在，哈希集中只有同层的子节点。（同父节点的同层去重）、
4-时空复杂度
一般说道回溯算法的复杂度，都说是指数级别的时间复杂度。
- 子集问题
  - 时间复杂度： $O(n × 2^n)$
    因为每一个元素的状态无外乎取与不取，所以时间复杂度为 $O(2^n)$ ，构造每一组子集都需要填进数组，又有需要 $O (n)$
  - 空间复杂度： $O (n)$
    递归深度为n，所以系统栈所用空间为 $O (n)$ ，每一层递归所用的空间都是常数级别，注意代码里的result和path都是全局变量，就算是放在参数里，传的也是引用，并不会新申请内存空间，最终空间复杂度为 $O (n)$ 。
- 排列问题
  - 时间复杂度： $O (n!)$
    可以从排列的树形图中很明显发现，每一层节点为n，第二层每一个分支都延伸了n-1个分支，再往下又是n-2个分支，所以一直到叶子节点一共就是 n * n-1 * n-2 * … 1 = n!。每个叶子节点都会有一个构造全排列填进数组的操作（对应的代码：result.push_back(path)），该操作的复杂度为 $O (n)$ 。所以，最终时间复杂度为：n * n!，简化为 $O (n!)$ 。
  - 空间复杂度： $O (n)$ ，和子集问题同理。
- 组合问题
  - 时间复杂度： $O(n × 2^n)$
    组合问题其实就是一种子集的问题，所以组合问题最坏的情况，也不会超过子集问题的时间复杂度。
  - 空间复杂度： $O (n)$
    同子集问题。
- 棋盘问题
  - N皇后问题
    - 时间复杂度： $O (n!)$
      其实如果看树形图的话，直觉上是O(n^n)，但皇后之间不能见面所以在搜索的过程中是有剪枝的，最差也就是O（n!），n!表示n * (n-1) * … * 1。
    - 空间复杂度： $O (n)$
      和子集问题同理。
  - 解数独问题
    - 时间复杂度： $O(9^m)$ ，m是’.'的数目
    - 空间复杂度： $O(n^2)$ ，递归的深度是 $n^2$