前言

C站的周赛已经很久没有新题了，已考过的题目我差不多都写过题解，若再重复写类似的文章，反而会降低博文质量分，而想要换个角度，却又难以找到动笔的欲望。所以虽然比赛发生在五一假期之前，但直到现在五一都过去了，我还没有想好该写什么。

本期考题如下：

1、隧道逃生 - 28期考过，题解

2、小艺照镜子 - 7、31、34期考过

3、大整数替换数位 - 37期考过，题解

4、清理磁盘空间 - 23期考过，题解

可以看到，关于最长回文子串的第二题，如果算上完全重复的31期和34期，已经考了四次了，足见这个知识点是多么基础且重要。虽然使用常见的中心扩展法也可通过本题，但作为有更高追求的选手，一定还想寻找和理解更加优化的复杂度为  的马拉车（Manacher's）算法。于是，借着这期周赛，我们一起来通俗地研究一下此算法。

题目描述：已知字符串str。 输出字符串str中最长回文串的长度。

序

要谈马拉车，我们不得不先理解中心扩展，因为马拉车算法实际上是在中心扩展法的基础上，通过使用静态数组（  数组），用空间换时间，省去了重复的比较和计算。于是，我们先来看中心扩展法是如何解决最长回文子串问题的。

顾名思义，中心扩展，就是根据回文字符串左右字符通过中心完全对称相等的特性，以某一点为中心，左右指针从小到大依次向两边扩散，检查左右字符是否相等。一直到左右字符不相等的时候停下，得到的字符串长度就是最长的回文子串的长度。

第一个问题

当回文字符串的长度是偶数时，并没有一个确切的中心点，因为中间对称的是两个字符。

所以并不能从某个中心点扩展开来，而是从中心两个字符扩展开来。

为了在代码上解决这个问题，通常有两种做法：一是分别检查奇偶字符串。示例代码如下。注意：此代码只是为了和后面的马拉车算法保持一致，以方便理解，实际上中心扩展法的实现方式可以有多种不同形式。

str = input()
n = len(str)
res = 1 # 最短的回文字符串就是一个字符
for i in range(n-1):
    j = 0
    if str[i] == str[i+1]: # 当回文子串的长度是偶数时
        while i - j > 0 and i + j < n - 2 and str[i-j-1] == str[i+j+2]:
            j += 1
        res = max(res, j*2+2)
    else: # 当回文子串的长度是奇数时，也就是存在中心字符
        while i - j > 0 and i + j < n - 1 and str[i-j-1] == str[i+j+1]:
            j += 1
        res = max(res, j*2+1)
print(res)

第二种方法就是把原始字符串“改造”一下，在字符串的首、尾及每个字符的间隔各加入一个特殊字符，将其构造成一个无论何种情况都存在中心点的字符串。以特殊字符“#”为例，我们可以将字符串构造成如下图所示：

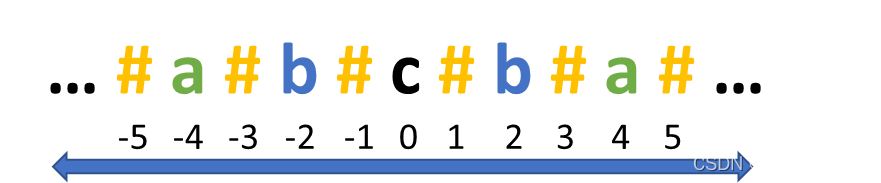
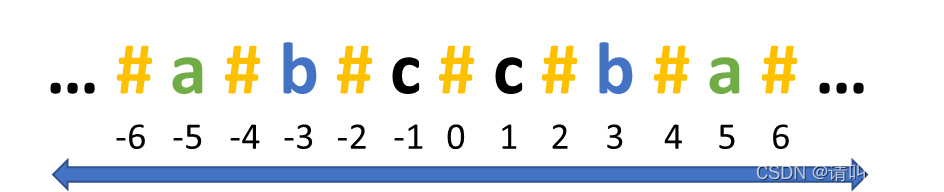
当回文串长度为奇数时，中心点是某个字符，当长度为偶数时，中心点是我们构造的特殊字符“#”。于是，我们在上面的代码稍作修改，同样的逻辑，代码量也随之减少：

str = '#' + '#'.join(input()) + '#' # 构造字符串
n = len(str)
res = 1
for i in range(n-1):
    j = 0
    while i - j > 0 and i + j < n - 1 and str[i-j-1] == str[i+j+1]:
        j += 1
    res = max(res, j) # 只需记录一半的长度 j，就是原始字符串中回文串的长度
print(res)

由于我们改造了原始字符串，所以实际回文子串的长度只有遍历中的一半，也就是  ，这也是我们的代码可以简化的原因之一。

实际上，使用上述中心扩展法已经可以轻松 AC 本题了。让我们一起看看还能如何优化吧。

马拉车优化了什么？

可以看出，如果字符串的长度是 ，需要分别以  个字符为中心，进行扩展检查。而每次检查，都需要检查 0 （当中心为左右首字母时） 到  次，所以中心扩展法的渐进算法复杂度是 。

但是，中心扩展法实际的计算次数并没有达到 。比如在极端情况，当字符串中没有回文子串时，中心扩展法的时间复杂度实际上也是 。——想象一下上面的第二段代码，内层while循环由于不满足左右字符相等的条件，所以并不会执行。

那么优化的空间在哪儿？

我们来看另一个极端情况，假设字符串是由同一个字符组成，如果使用中心扩展法，实际需要计算多少次呢？

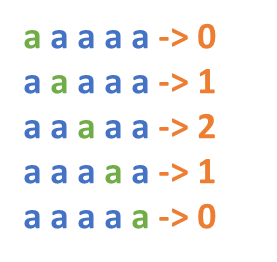
上图以长度为 5 的字符串为例，当检查完中间的 “a” 时，实际上就已经完成了所有字符的比较，所以，似乎、隐约觉得中间 “a” 之后的中心点是可以优化的。

我们再看一例，假设我们检查的是一个长度为7的回文字符串，如下图所示：

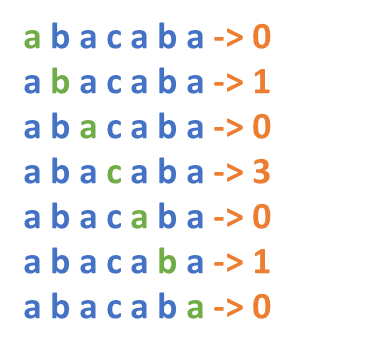
当检查完这个回文串的中心点“c”时，实际上右边的字符都已经被比较过了。从实际比较的次数也可以看出来，以“c”右边的字符为中心点进行查找和比较的次数，与左边的相同。也就是说，如果已经确定了一个大的回文串，那么在其中心点（）的右边，右边界（）的左边，以这些字符作为中心点所需要的扩展比较次数，应该有一部分已经在中心点（）左边与其相对应的字符作为中心点时比较过了。

上面说的可能还是太复杂了，我们画图来说明。

假设已经通过中心扩展确定了一个较大的回文子串（从  到 ），也就是说从这个回文子串的中心点  到右边界  之间的字符已经被比较过一次。

继续循环，将  到  之间的位置为  的字符作为中心点进行扩展检查时，在  与  之间，必定存在一个  的镜像点  ，——回文串都是对应的。

由于我们在检查  之前，必定已经检查过点 ，所以关于点  的回文子串的大小，有两种可能：

1. 以点  为中心扩展的回文子串大小不超过这个较大回文子串的左边界  。由于回文串的对称性，点  为中心进行扩展的回文子串必然与  相等。也就是说，从点  到点  之间的字符都可以不用再检查了。

2. 以点  为中心扩展的回文子串大于等于这个较大回文子串的左边界  。这种情况下，由于我们还没有比较过  之后的字符，所以不能确定以点  为中心进行扩展的回文子串是否会大于  。所以点  到  之间的字符也都不需要再检查，只需要扩展检查  之后的字符即可。

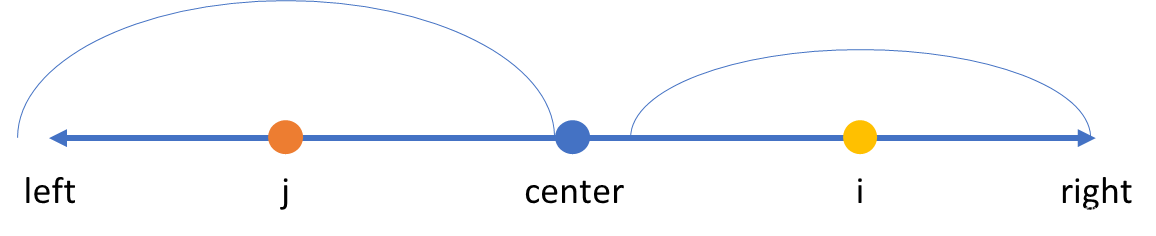
综上所述，马拉车算法优化的部分，其实就是通过借助回文字符串的对称性，优化了  到  之间位置的中心扩展部分。——因为其中一部分已经在  到  之间扩展比较过了。

如此，我们可以发现，从左往右进行中心扩展，已经比较过的字符，都不需要再进行比较了，也就是说，所有位置的字符都只需要检查一次，所以马拉车的算法复杂度在任何情况下都是 。——当然，如果仔细数的话，比较次数应该是  的常数倍。

实现

知道了马拉车的原理（大概），我们来捋一捋如何用代码实现。

1. 由于我们是从左向右依次选择中心点进行扩展比较，所以很显然，需要使用一个  循环，而  就代表了字符串的每个位置。

2. 我们还需要记录当前已经遍历过的  所发现的最大回文子串，也就是  和  的位置。由于对称性，我们不需要再记录  的位置，因为  。同样地，点  的位置也可以通过计算得到： 。

3. 前面说过，我们要优化的部分是  到  之间的字符进行中心扩展的比较部分。所以我们需要比较  和  的关系：如果 ，说明存在优化的可能。

4. 最关键的，我们要记录左边点  为中心的回文子串的大小，从而决定了右边点  为中心时，可以省去多少比较位置。所以，我们引入了一个数组  ，用来记录每个点为中心时，最大回文子串的半径。

将上面几点带入之前的代码，更新如下：

str = '#' + '#'.join(input()) + '#' # 构造字符串
n = len(str)
p = [0] * n # 初始化 P 数组
center = right = 0 # 初始化较大回文串
for i in range(n):
    if i < right:
        j = 2 * center - i # 通过中心计算对称的位置 j
        p[i] = min(right - i, p[j]) # 根据 j 为中心的回文串大小，有两种可能
    while i - p[i] > 0 and i + p[i] < n - 1 and str[i - p[i] - 1] == str[i + p[i] + 1]: # 在此基础上再进行扩展
        p[i] += 1
    if i + p[i] > right: # 如果目前为止最大回文串的半径大于i，说明存在优化的可能
        center, right = i, i + p[i] # 更新最大回文串的中心和右边界
print(max(p))

后记

这篇关于马拉车算法的博文只能算是粗略的分析了，如果需要完整学习，建议搜索查看网络上其他文章。但是如果已经看过其他文章但是却还是一知半解，但愿你会从这篇文章里get到一点启发。