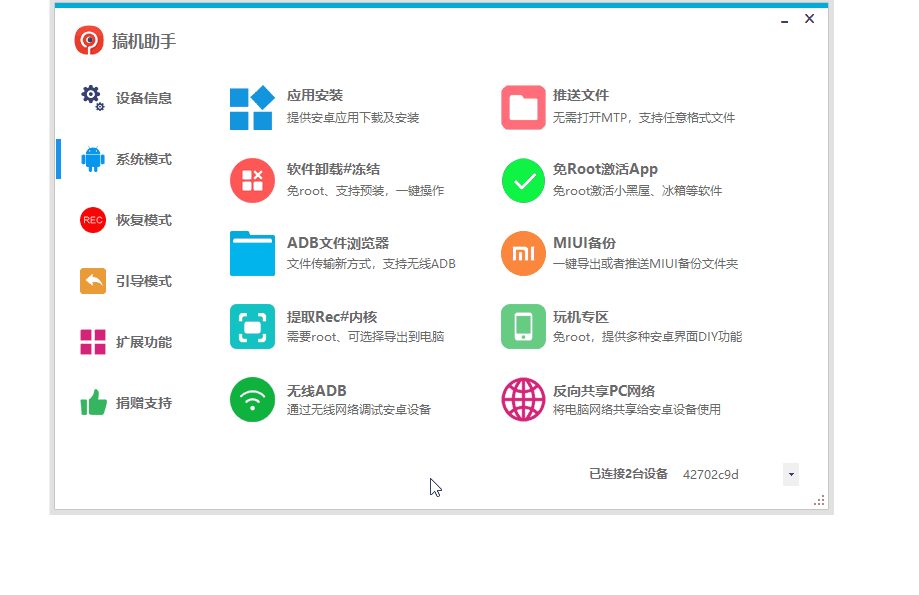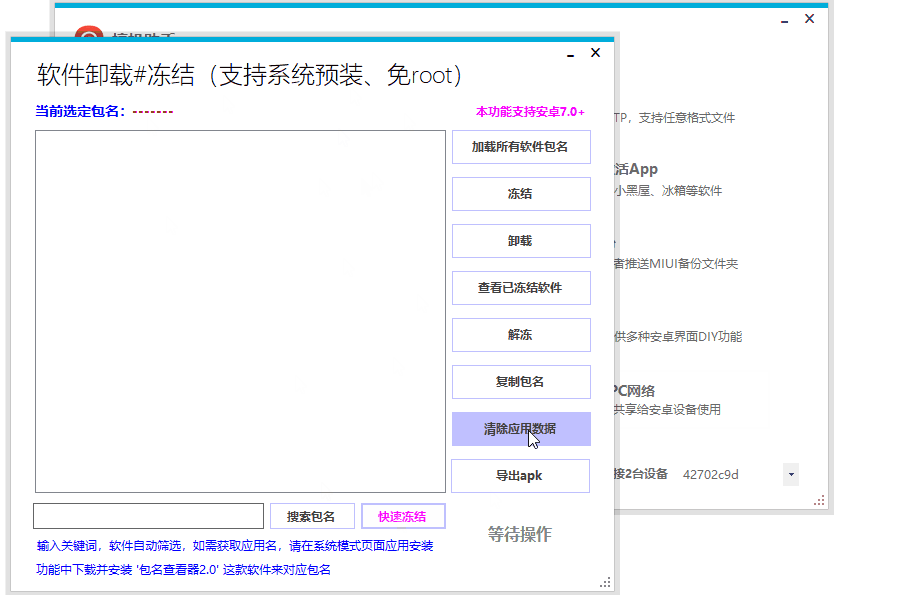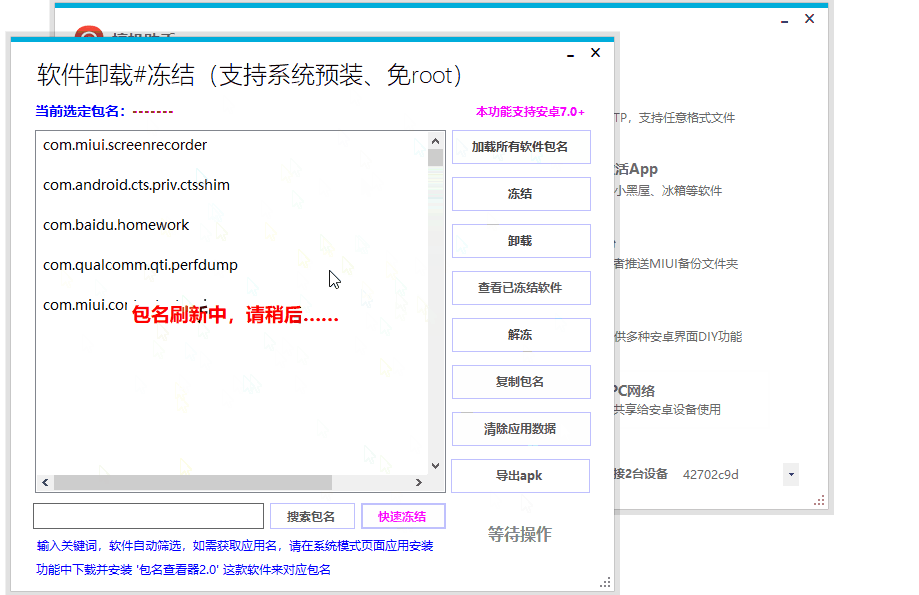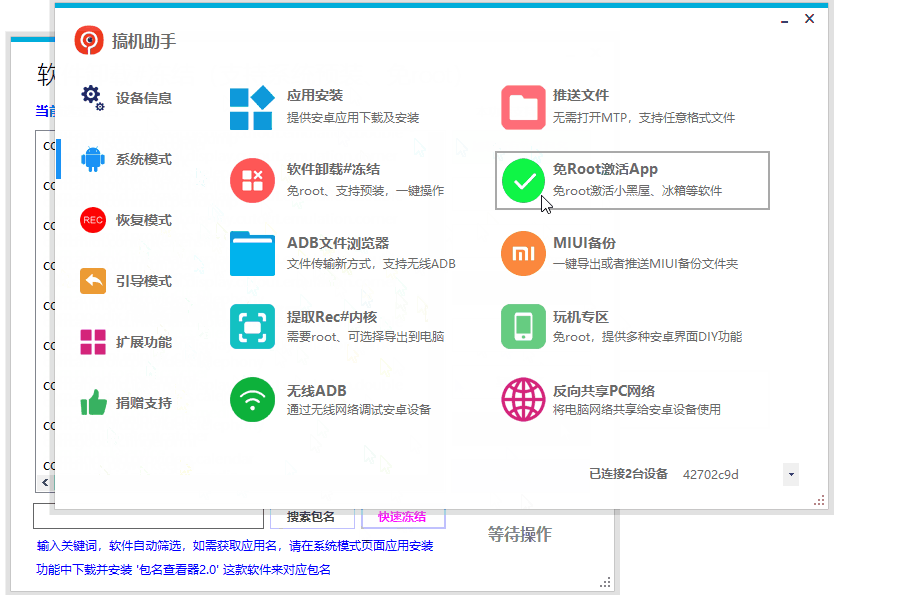
1. 梯度
将导数拓展到向量。
1. 标量对向量求导
x是列向量,y是标量,求导之后变成了行向量

ps: x1^2 + 2x2^2 这个函数可以画成等高线,对于(x1,x2)这个点,可以做等高线的切线,再做出正交方向(2,4),这个正交方向和梯度是一样的,也就是梯度和等高线是正交的,意味着梯度指向的是值变化最大的方向
样例
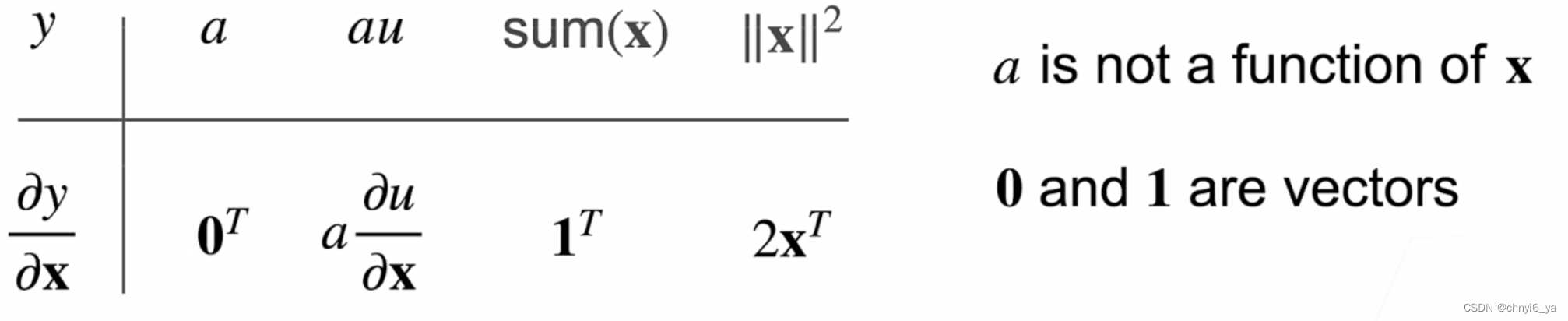
ps:1T,0T都是行向量(默认为列向量,使用转置后变成了行向量)
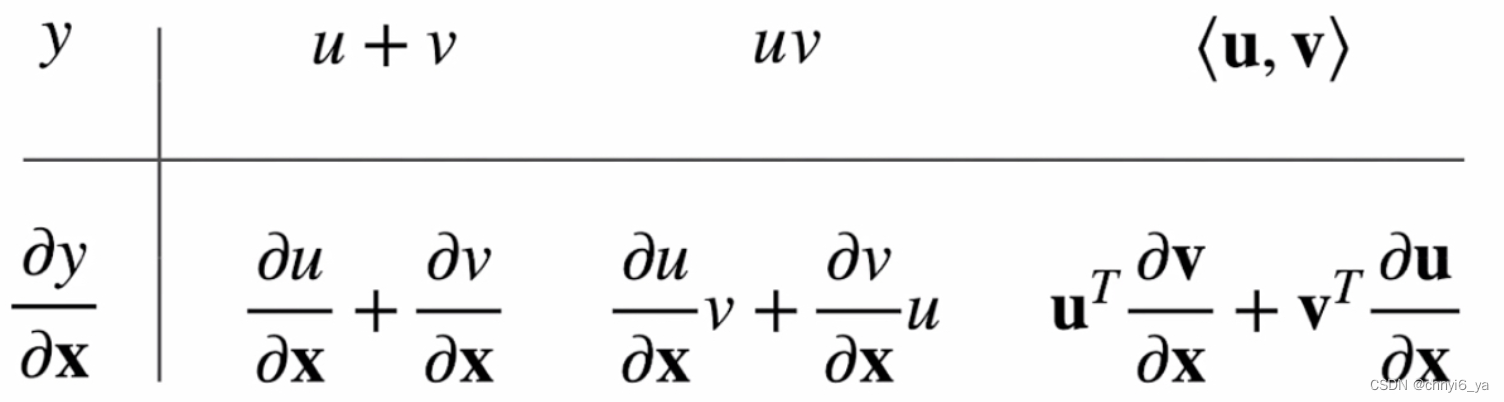
对于最后一个<u,v>,对x求导后,得到的是,行向量 * 矩阵 + 另一个行向量*矩阵
2. 向量对标量求导
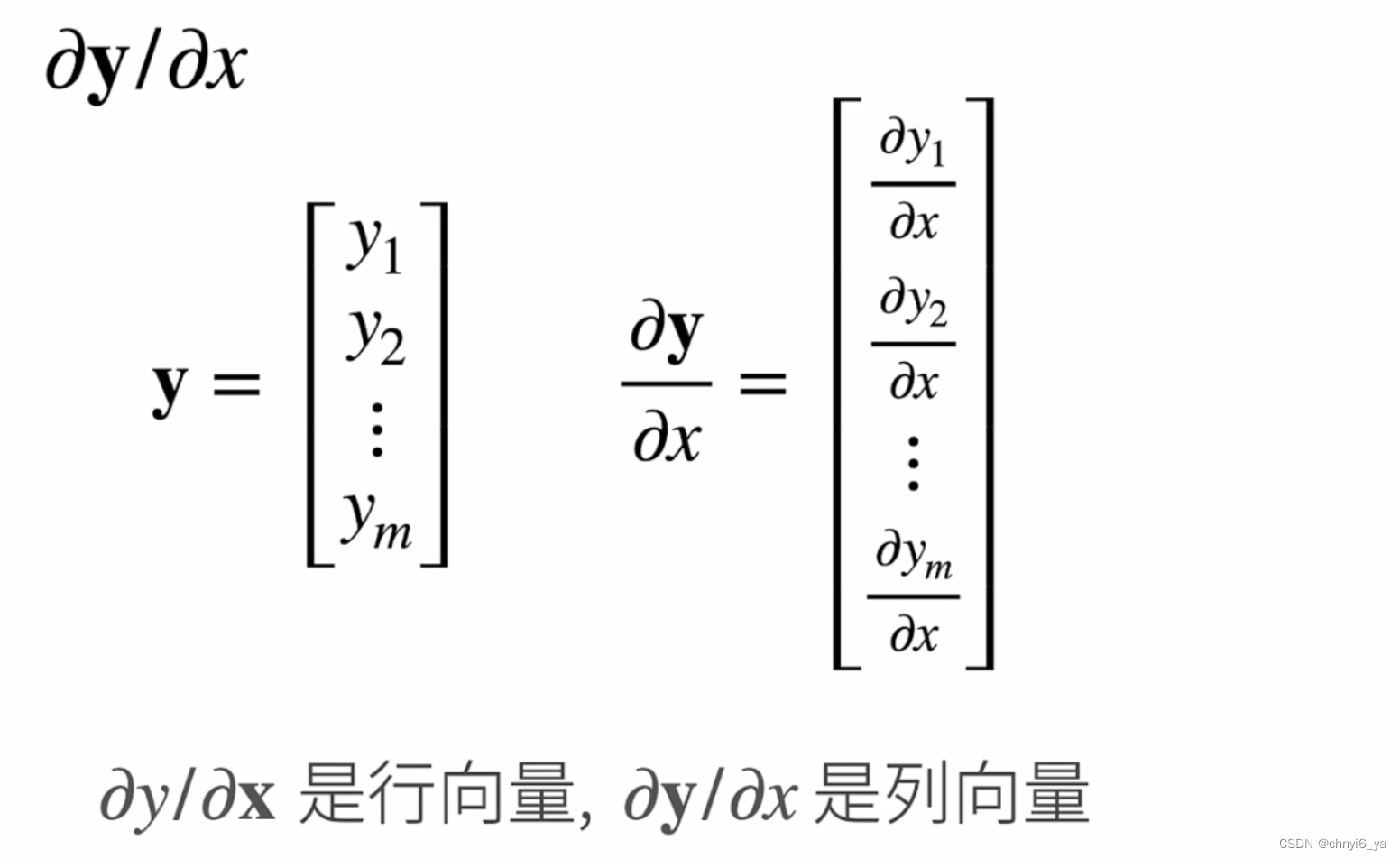
当向量是列向量时,对标量求导之后,得到的结果也是列向量。
3. 向量对向量求导
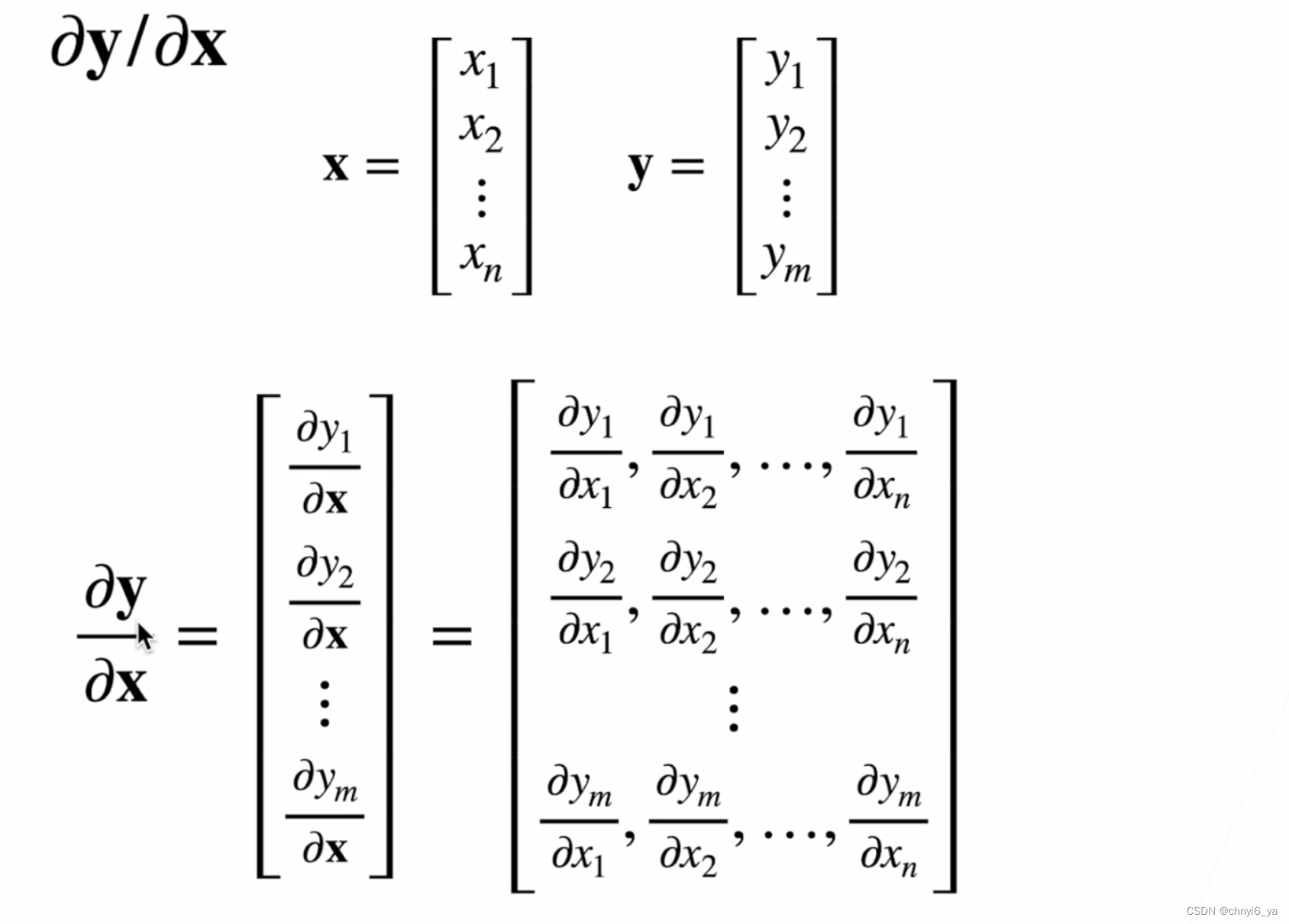
因为y本身是列向量,因此对x求导,先把y拆解成列向量的形式,之后每一个yi关于向量x的导数都是行向量,最后就变成了矩阵。
样例
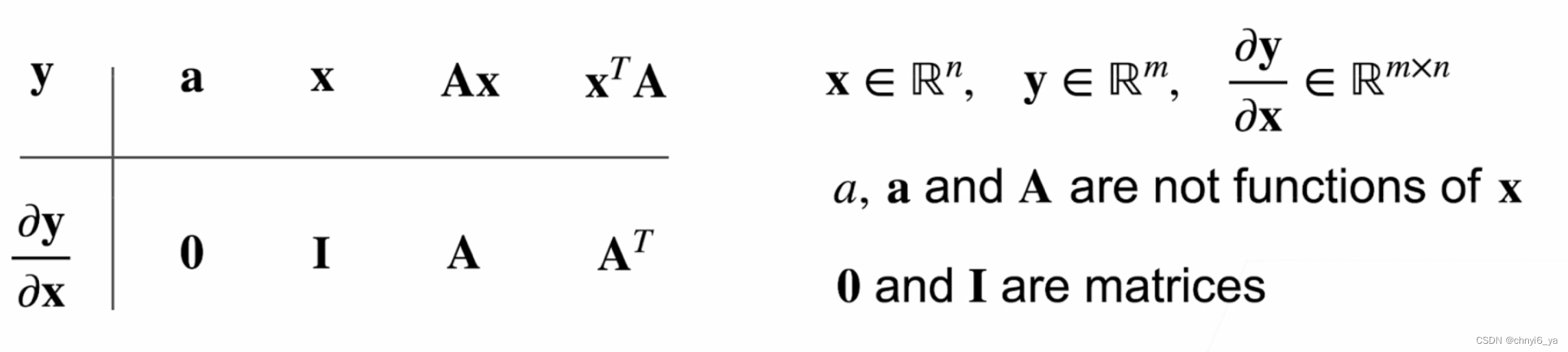
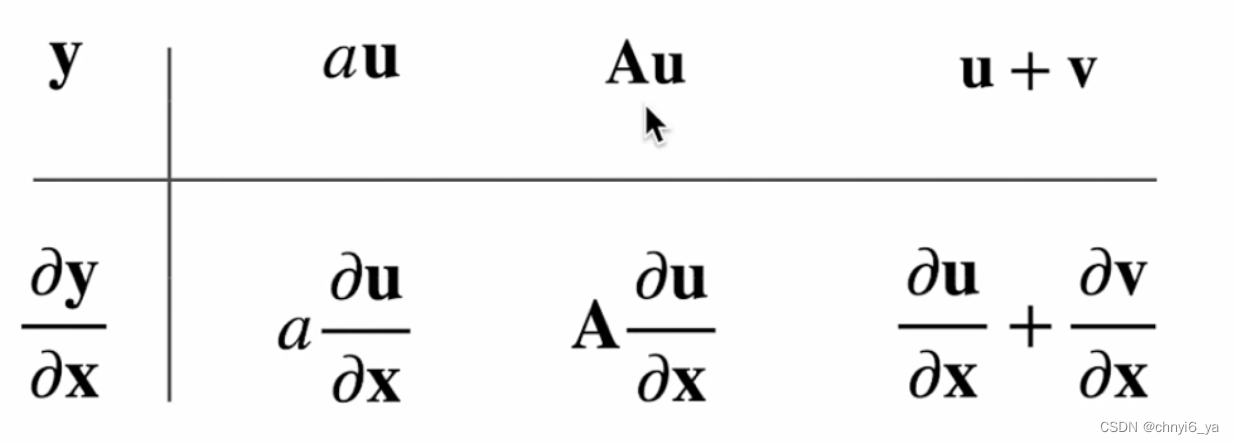
4. 拓展到矩阵

5. 链式法则
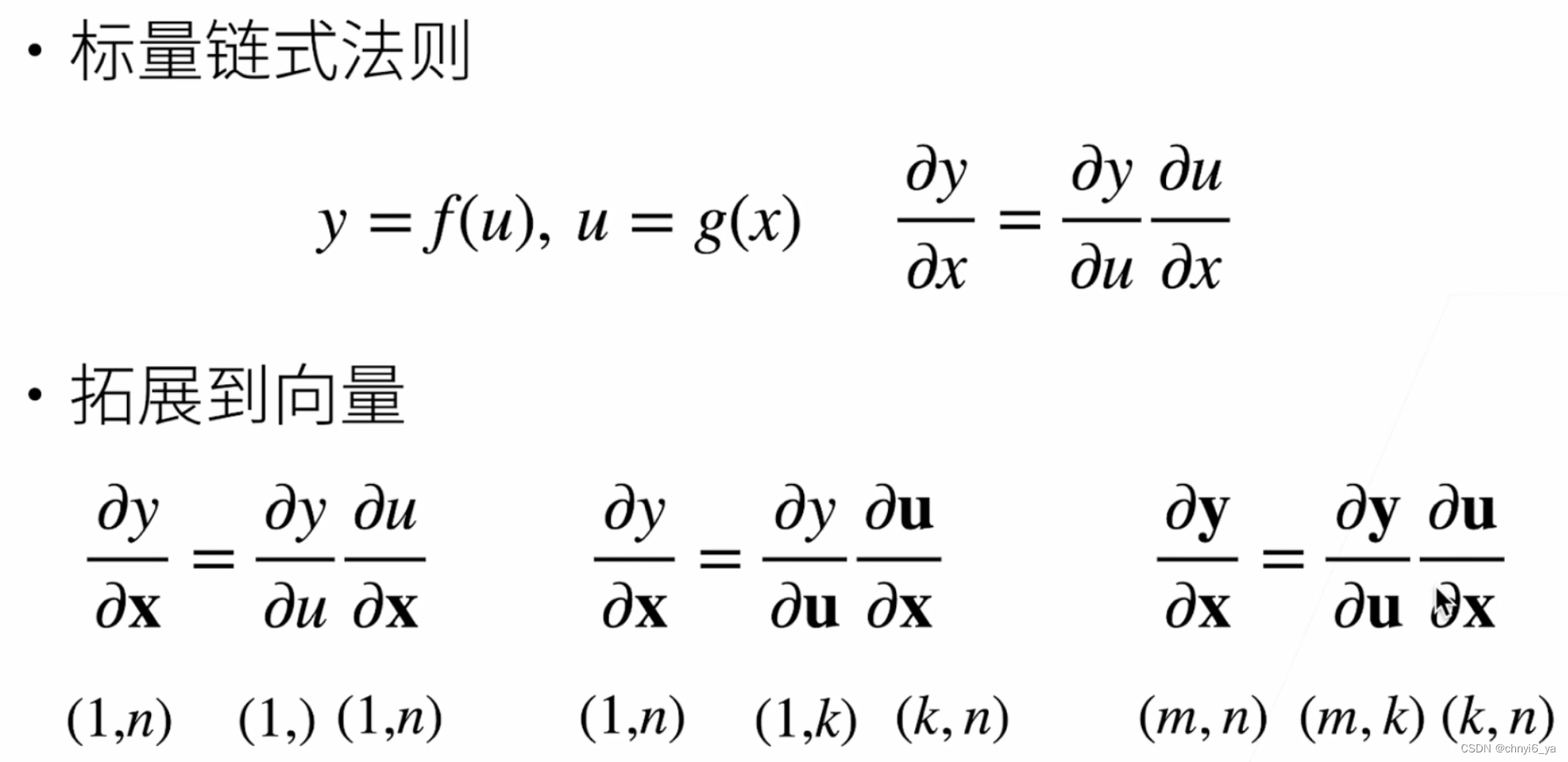
例子1如下:
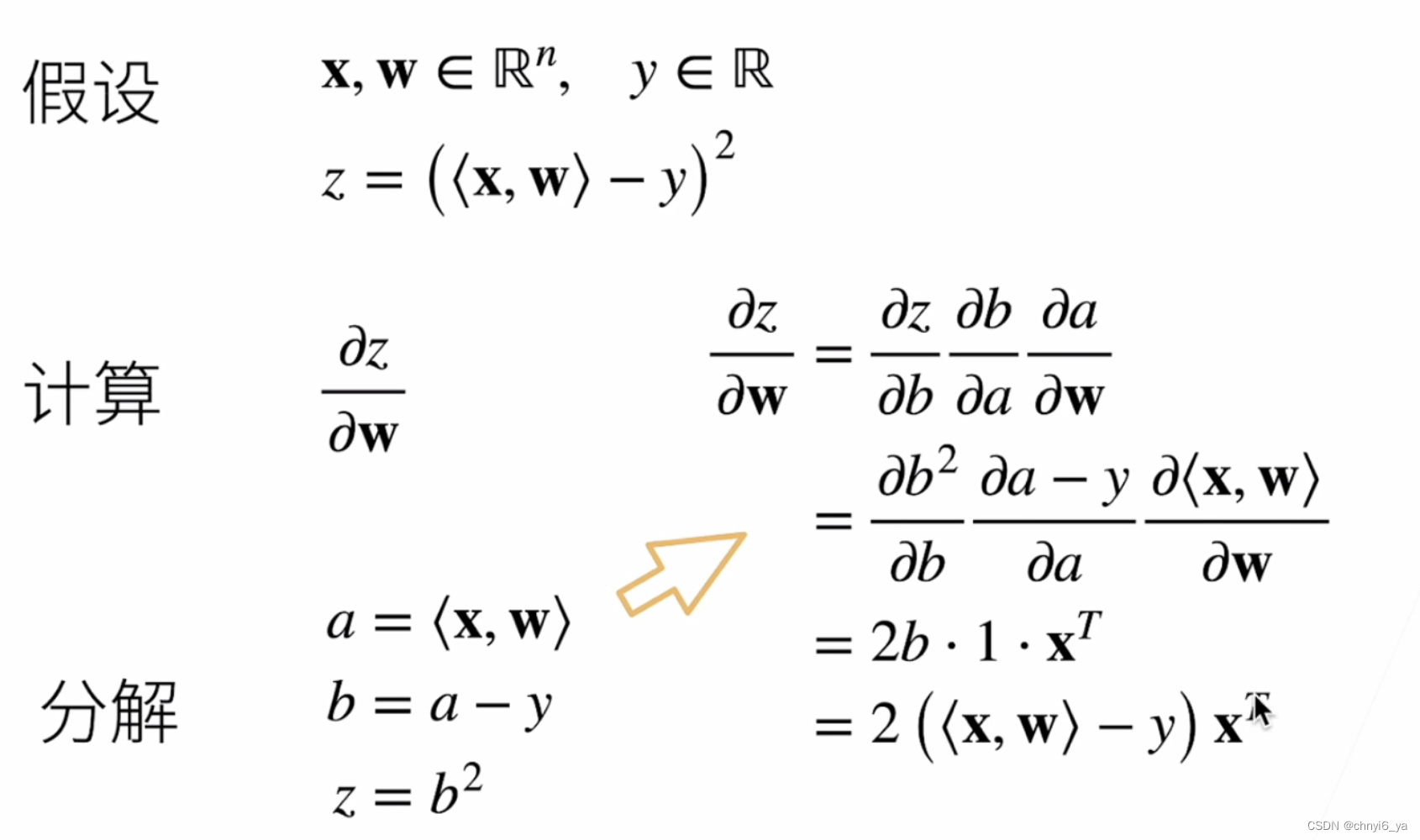
解释怎么得到的x的转置:因为<xw>是内积,得到的是一个标量,标量对向量w求导,得到的是行向量,因此是转置。
例子2如下:
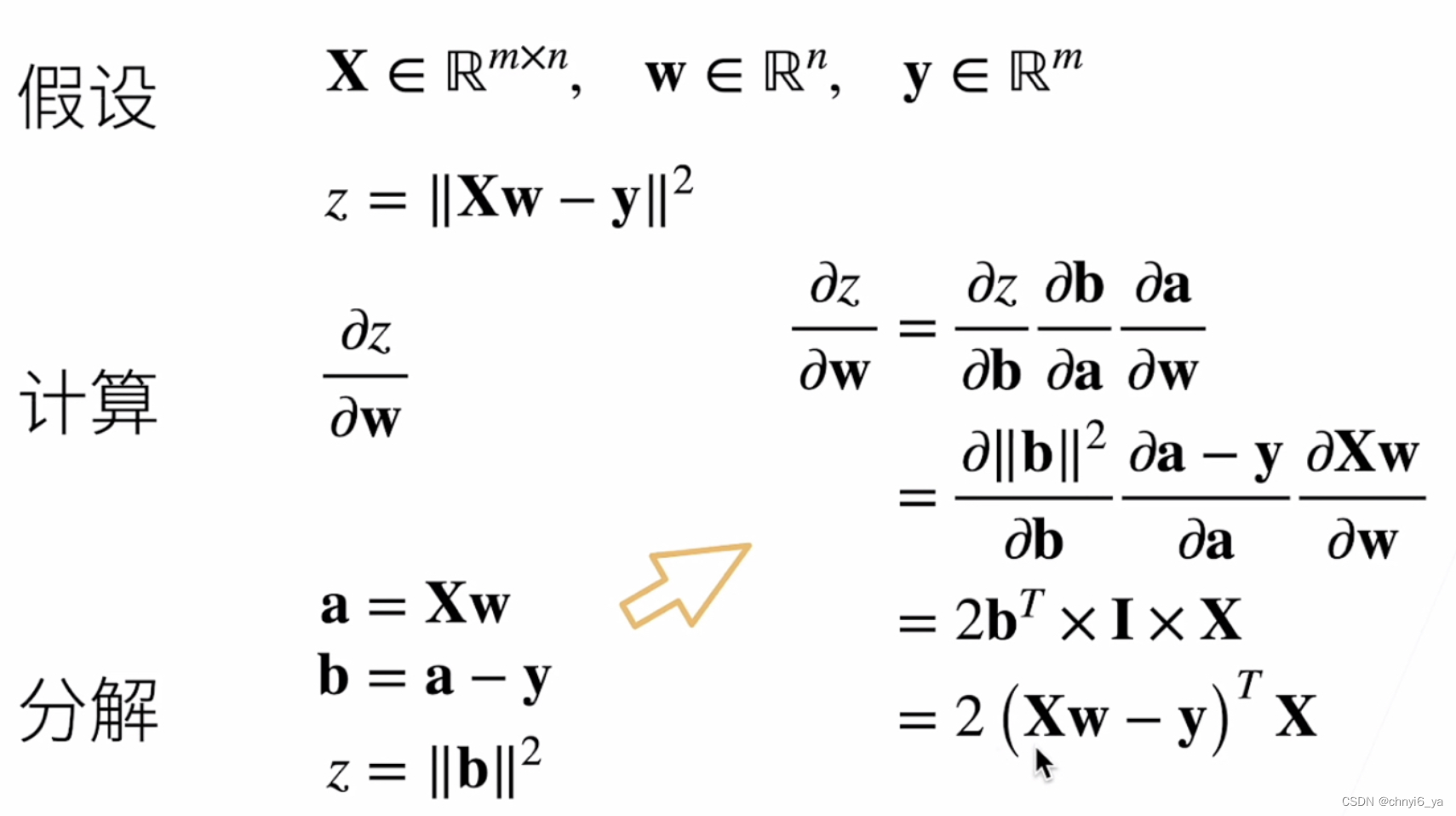
X是mn的矩阵,w是n1的列向量,y是m1的列向量,因此Xw就会得到m1的列向量,也就是说a就是m1的列向量,那么b也是m1的列向量。
- 第一项得到的是b的转置,是因为标量对向量求导得到的是行向量,所以对b这一列向量转置得到行向量
- 第二项,a对自身求导得到单位向量,也可以说是单位矩阵
- 第三项,是m1的向量对n1的向量求导,向量对向量求导,得到的是矩阵,因此最后得到m*n的矩阵,也就是X矩阵
6. 自动求导的两种模式

关于反向累积:
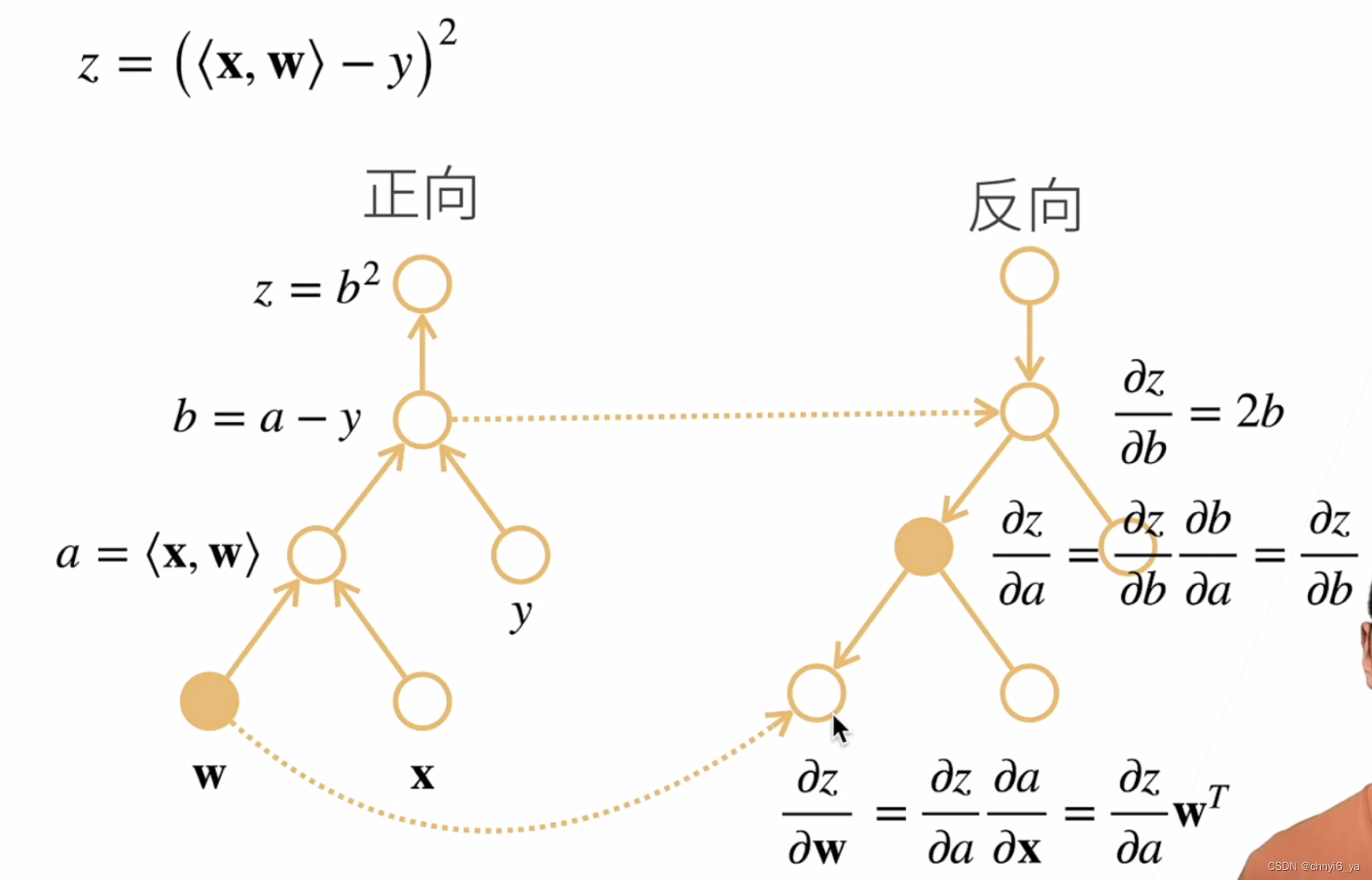
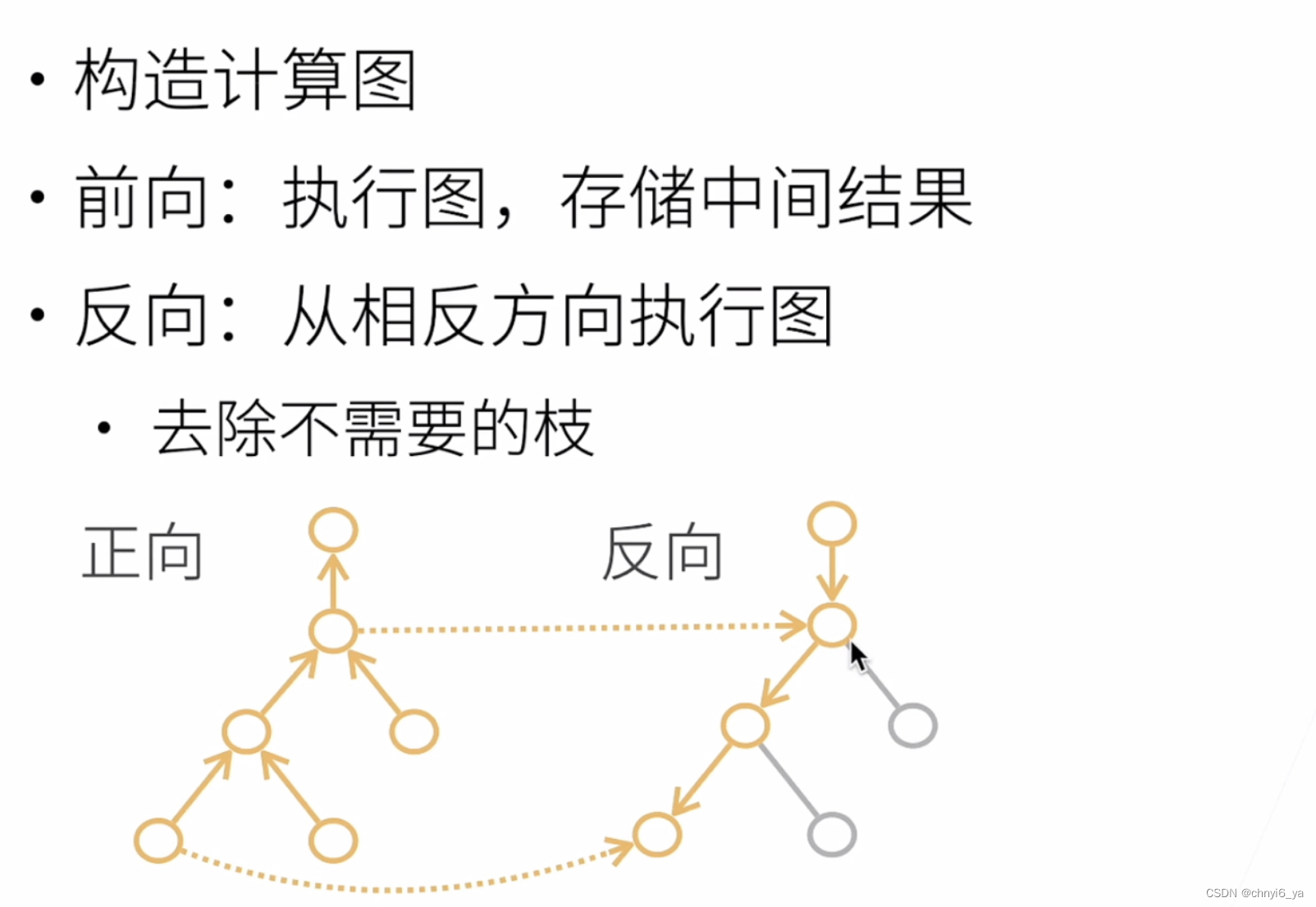
分为前向和反向,正向就是求复合函数的值,反向就是求偏导和梯度