文章目录
- 最长回文字串
- 动态规划
- 代码示例
前篇:
(1)初识动态规划
最长回文字串
传送门:
https://leetcode.cn/problems/longest-palindromic-substring/description/
给你一个字符串 s,找到 s 中最长的回文子串。
s ="babab”
结果:“babab”
解析,这是一道典型的动态规划的问题,但是如果你不知道动态规划,你会怎么做 ?
你可能会想到:依次截取字符串s中的每一个子字符串,然后每一次都比较这个子字符串是不是回文的,并且记录字串最大长度和起始下标,这样做固然可以。
但是!! 它的时间复杂度会非常高,把字符串切成每一种不同的字符串,仅仅 “babab” 这五个长度的字符串就有这些可能性,我们需要每次都判断它是否是回文字符串,并且记录,这对于leetcode的测试案例来说是不可能完成的!
他的时间复杂度是O(n^3),在check判断回文里还需要进行一次完整的遍历。因此这种方式是不要可行的。
b
ba
bab
baba
babab
a
ab
aba
abab
b
ba
bab
a
ab
b
完整代码如下:
class Solution {
public:
bool check(string s)
{
int left=0,right=s.size()-1;
while (left<right)
{
if (s[left++]!=s[right--])
{
return false;
}
}
return true;
}
string longestPalindrome(string s) {
int len=0;
int max_len=0;
int start=0;
for (int i=0;i<s.size();i++)
{
len=1;
for (int j=i;j<s.size();j++)
{
string temp=s.substr(i,len);
if (check(temp))
{
if (len>max_len)
{
max_len=len;
start=i;
}
}
len++;
}
}
return s.substr(start,max_len);
}
};
动态规划
既然是回文串,那么我们不妨想一想回文串有什么性质呢?
以 “babab” 为例。
如果它是回文串,并且长度大于 2,那么将它首尾的两个字母去除之后,它仍然是个回文串: aba是回文串 —> babab 也是回文串,因为首位两个b也相等。
我们可以用 P(i,j)表示字符串s中 从 i 到 j 的字符组成的串,用s[i : j]表示这个串。
P(i,j)可以表示两种情况:
- true: s[i] -> s[j] 构成回文的字符串。
- false:非法的情况。
其中false非法的的情况又分为这两种情况:
- s[i] -> s[j] 本身不构成回文串
- i,j下标不合法,在动态规划中我们需要经常处理下标越界的情况。
状态转移方程:
P(i,j)=P(i+1,j-1)+ (s[i] == s[j])
也就是说:判断第s[i] -> s[j] 构成的字串是否是回文串
- 需要判断第 s[i+1] -> s[j-1] 是否构成回文串
- 判断第 s[i] 和 s[j] 首尾两个字符是否相同。

我们来进一步分析这个状态转移的公式:
前提准备:
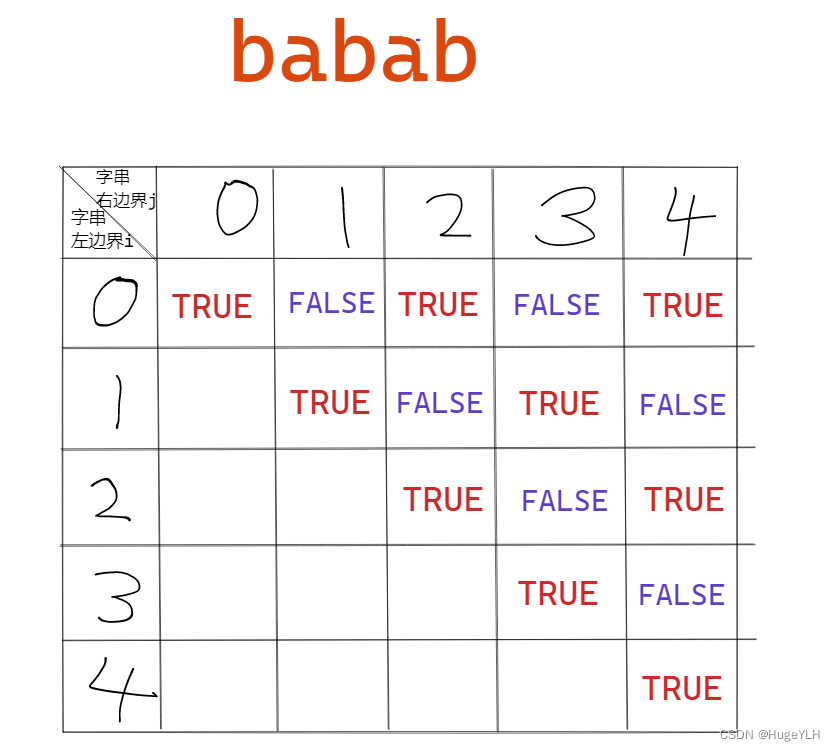
- 我们创建dp二维数组表示他们的不同i,j时,i,j所对应的首尾子串的回文状态。
- 我们首先从列开始,从上往下填充;然后从行开始,从左往右填充。
- 当 i==j的时候,可以看作左边界与有边界相等,因此这个字串就一个字符,这一定构成回文串,所以
dp对角线元素一定是true,即是回文串。 - (0,1)表示的字符串长度等于2,即比较s[0] == s[1],很明显不同,填充为 false
- (0,2)的状态可以由首尾两个字符的相等性(true)与他们缩小之后的子串(true)判断,bab显然是回文的,因此可以由状态方程之前存储的值得到(0,2)的状态,填充为true
- (1,2),他们的长度等于2,而且两个字符不相等,填充为false.
- (0,3):由(1,2)+ s[0]==s[3] 的状态确定。(1,2)已经被填充为了是false,因此只需比较首尾字符是否相等即可,填充为false。
- (1,3):由(2,2)+s[1]==s[3]状态确定,填充为true。
- (2,3):长度等于2,只需比较 s[2]==s[3],填充为false。
- (0,4):由(1,3)+ s[0]==s[4]的状态确定。(1,3)已经被填充了true,再加上首尾字符相同,所以填充true。
- (1,4):由(2,3)+ s[1]==s[4]状态确定,填充为false。
- (2,4):由(3,3)+ s[2]==s[4]状态确定,填充为true。
- (3,4):长度小于2,只需比较 s[3]==s[4],填充为false。
代码示例
class Solution {
public:
string longestPalindrome(string s) {
int n=s.size();
//---------------Tip1
if (n==1)
{
return s;
}
vector<vector<bool>> dp(n,vector<bool>(n));
for (int i=0;i<n;i++)
{
dp[i][i]=true; //对角线一定为true,相等于i==j
}
int start=0,max_len=1;
//---------------Tip2
for (int L=2;L<=n;L++)
{
for (int i=0;i<n;i++)
{
//--------------Tip3
//j-i+1=L
int j=L+i-1;
if (j>=n)
{
//右边界越界,直接退出
break;
}
//首尾相等,填充true。那么不相等就填充false
if (s[i]!=s[j])
{
dp[i][j]=false;
}
else
{ //到了这个else里面,那么就意味着 s[i] == s[j] 子串首尾字符是相同的
// j - i < 3: 填充长度小于等于3的字符串的状态
//长度小于等于3的长度为2的为true( s[i]=s[j])
//长度为3也是true(s[i] ==s[j]) && 中间的单独的字符,一定构成回文串。
if (j-i<3)
{
dp[i][j]=true;
}
else
{//长度较长的则进入状态转换,由之前的状态转换得到。
dp[i][j]=dp[i+1][j-1];
}
}
//每次都要记录目标子串的长度与坐标
//1. 如果以 i为左,j为右的子串是dp[i][j]=true,则它是一个回文串
//并且长度大于之前记录的子串,则更新此最长的回文串。
if (dp[i][j] && j-i+1>max_len)
{
max_len=j-i+1;
start=i;
}
}
}
//根据得到的左边界坐标和长度得到目标子串
return s.substr(start,max_len);
}
};
需要注意的几个细节:
- Tip1. 当我们的s只有一个字符时,它一定是回文串,直接返回即可。
- Tip2. 我们根据子串的长度进而获得指定长度的子串进行依次填充dp数组,首先L 为2时,填充长度为2的子串的回文性;其次L为3,填充长度为3的字串…一直到最后L为5,填充长度为5的子串的回文性,本例中长度为5的字串即是 s 串本身。
- Tip3. 我们都知道,想要得到一个子串就需要某个特定的左边界 i 以及子串的长度,这样我们就能确定一个子串。在本题中我们不仅要获得这两个元素,还要获得 这个子串的右边界j:因为我们需要判断子串首尾两个字符是否相等,我们可以由 j - i + 1 = L(子串右边界下标 - 左边界下标 + 1 = 字串的长度),得到 j=L+i-1 ,即对应的右边界下标。