题目链接

牛客网在线oj题——二叉树的深度

题目描述

输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度，根节点的深度视为 1 。

数据范围：节点的数量满足 0≤n≤100 ，节点上的值满足0≤val≤100

进阶：空间复杂度 O(1) ，时间复杂度 O(n)

假如输入的用例为{1,2,3,4,5,#,6,#,#,7}，那么如下图:

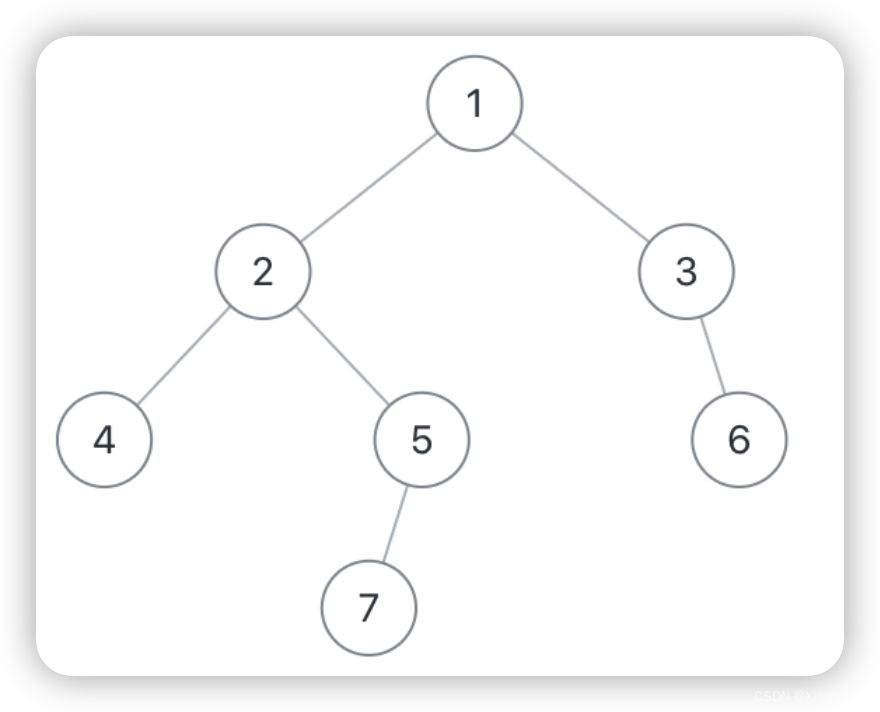
题目示例

示例1

输入：
{1,2,3,4,5,#,6,#,#,7}

返回值：
4

示例2

输入：
{}

返回值：
0

解题思路一

使用广度优先搜索，将二叉树进行层序遍历，每遍历一层就将depth++

广度优先遍历需要借助队列，首先将根节点加入到queue中，然后每次先确定队列的大小size，然后弹出size个元素，分别将这些元素的左子树和右子树加入到队列中（如果不为null）

上面每次弹出size个元素的过程就是遍历一层的过程，因此此时将depth++即可

例如：

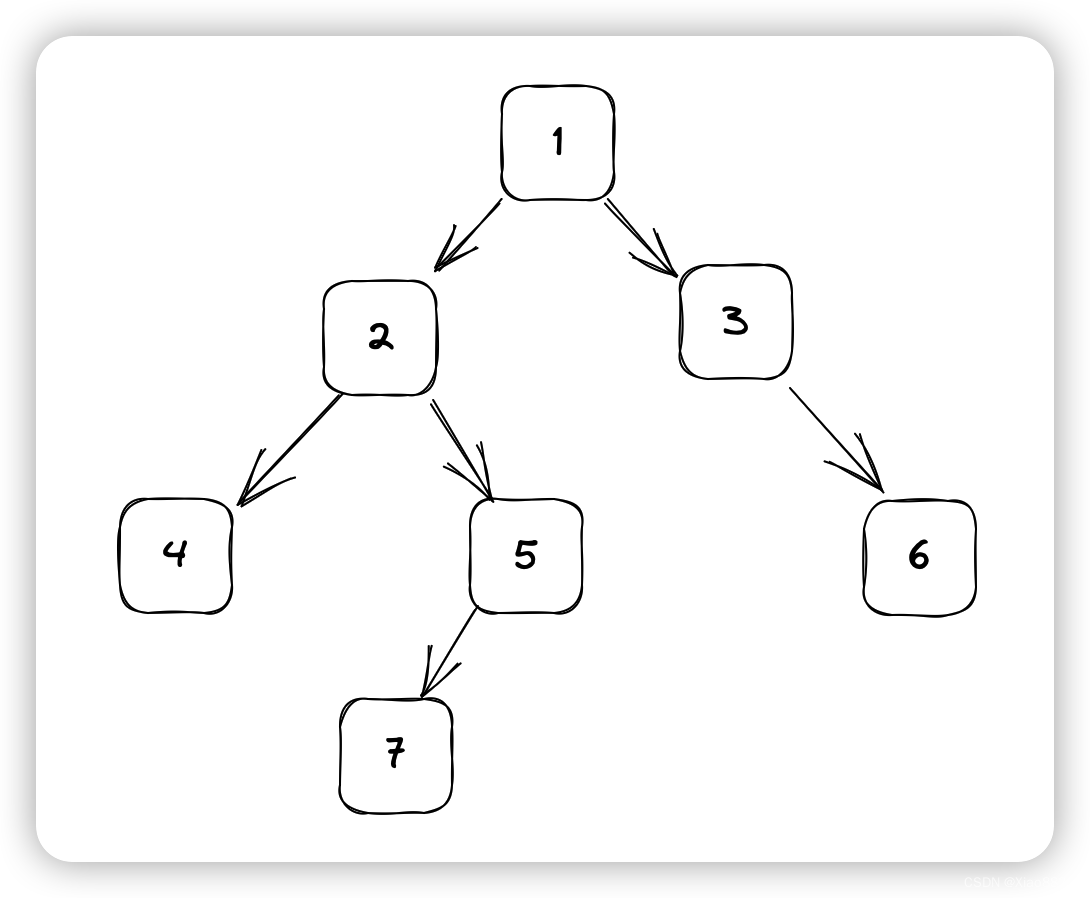
首先将根节点加入队列中，depth++

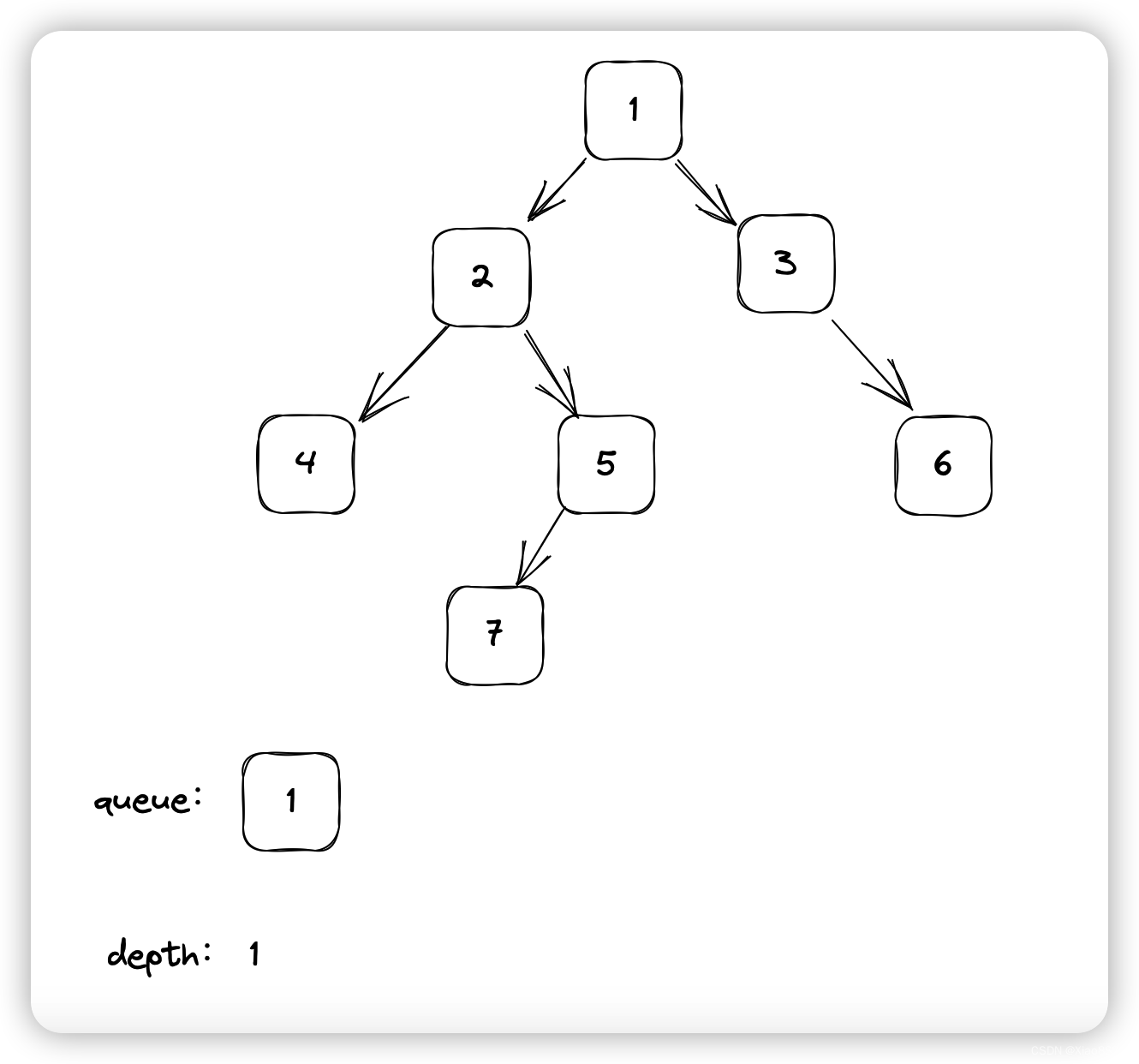
现在queue的长度是1，弹出1个元素，将其左子树和右子树添加进队列，depth++

现在queue的长度是2，弹出2个元素，将其左子树和右子树添加进队列，depth++

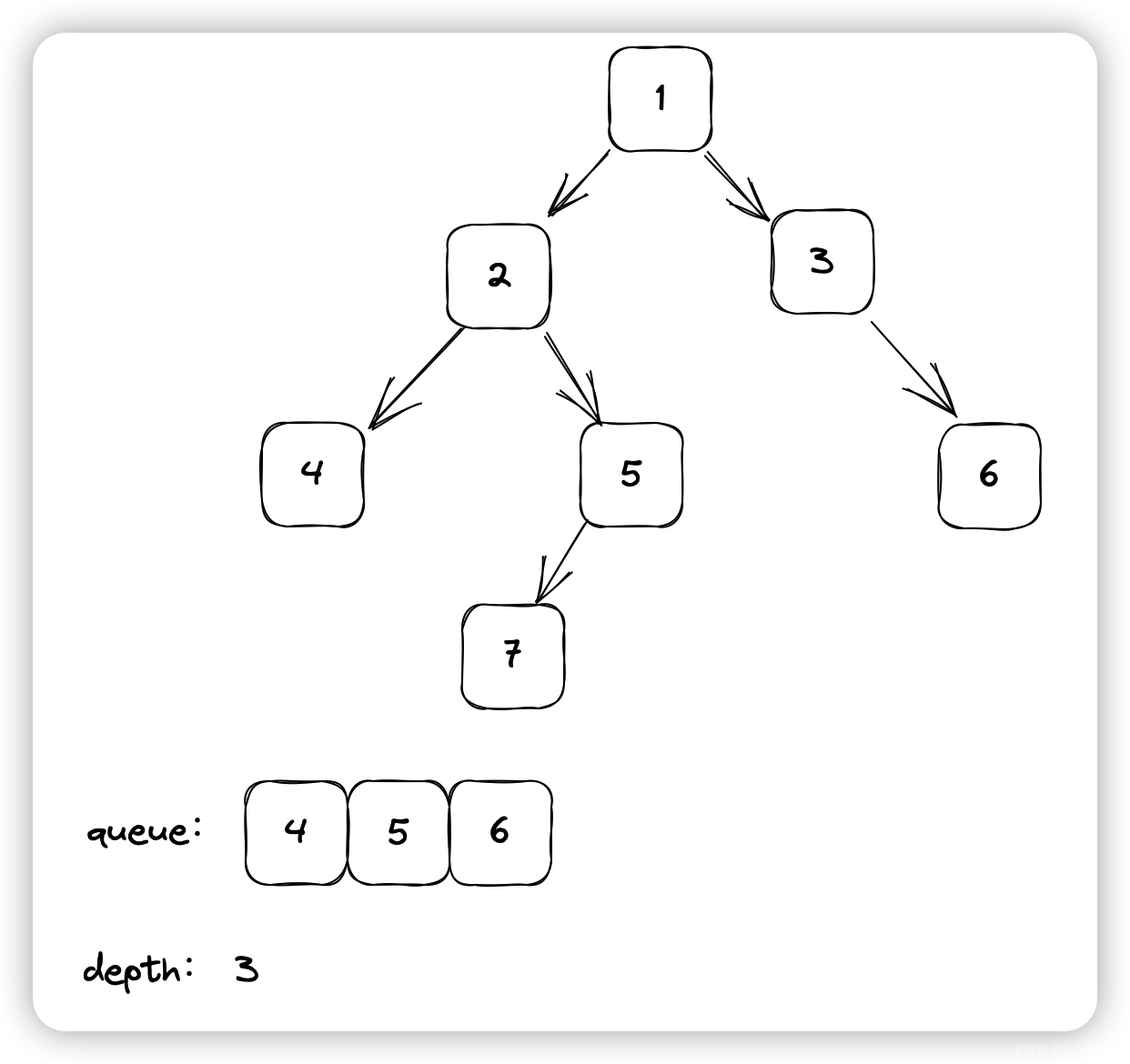
现在queue的长度是3，弹出3个元素，将其左子树和右子树添加进队列，depth++

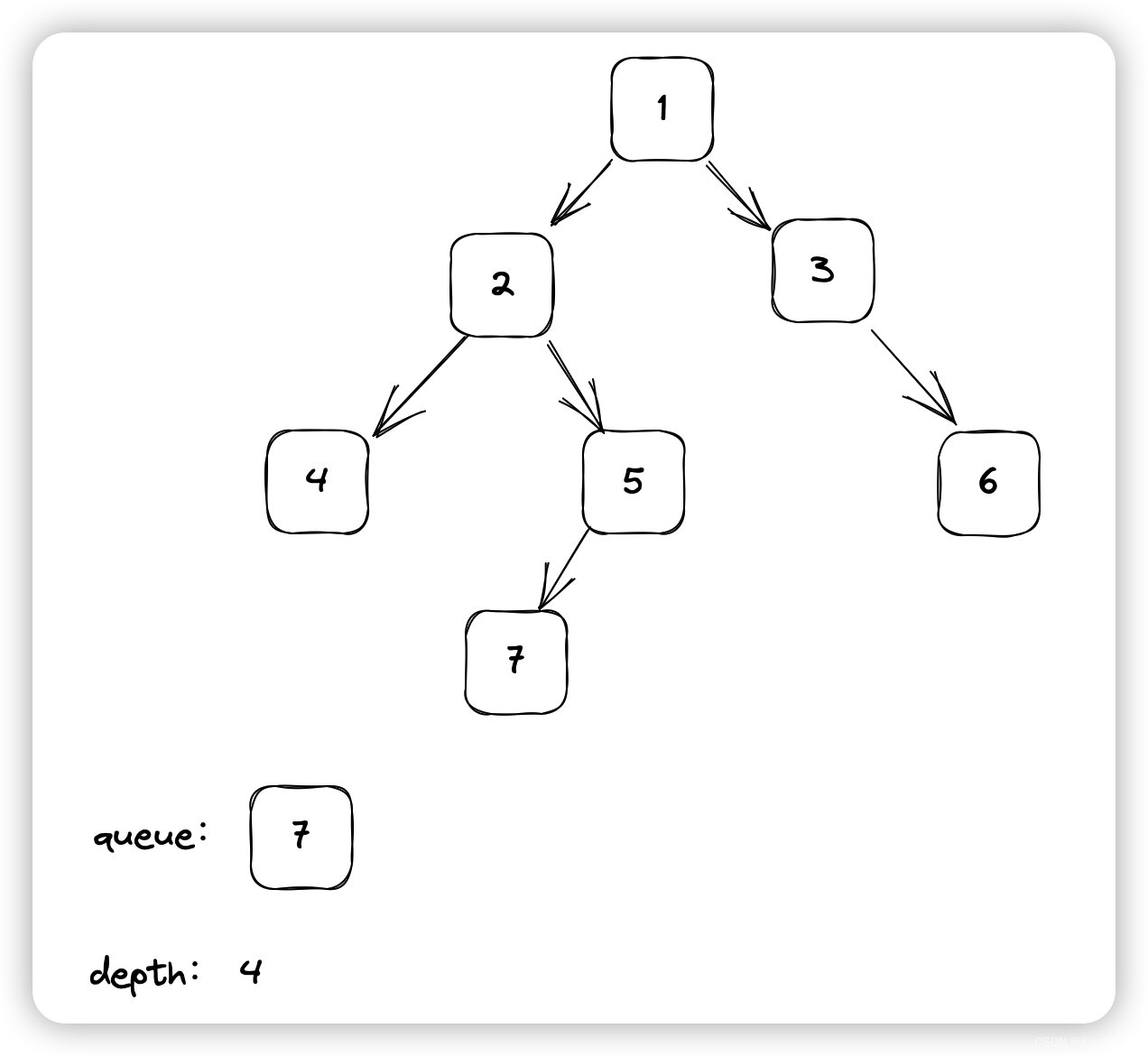
现在queue的长度是1，弹出1个元素，此时该元素左子树和右子树都为null，不再向队列中添加元素，循环结束，depth = 4

方法一完整代码

import java.util.*;
/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
public class Solution {
    public int TreeDepth(TreeNode root) {
       if(root == null){
            return 0;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        int depth = 0;
        while(!queue.isEmpty()) {
            int size = queue.size();
            depth++;
            for (int i = 0; i < size; i++) {
                TreeNode cur = queue.poll();

                if (cur.left != null) {
                    queue.add(cur.left);
                }
                if(cur.right != null){
                    queue.add(cur.right);
                }
            }
        }
        return depth;
    }
}

思路二

深度优先搜索，分别确定左右子树中深度的较大值

使用递归分别确定节点的左子树高度和右子树高度，每次递归到下一层节点都需要将depth + 1，如果此时depth的长度大于max，就将max的值更新为depth，这样就可以返回左右子树高度的较大者

方法二完整代码

/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }
}
*/
public class Solution {
    public int TreeDepth(TreeNode root) {
       if(root == null){
           return 0;
       }
       
       int depth = 0;
       int[] max = new int[1];
       max[0] = 0;
       TreeDepthHelper(root, depth, max);
       return max[0];
    }

    private void TreeDepthHelper(TreeNode root, int depth, int[] max) {
        if(root == null){
            if(max[0] < depth){
                max[0] = depth;
            }
            return;
        }
        TreeDepthHelper(root.left, depth + 1, max);
        TreeDepthHelper(root.right, depth + 1, max); 
    }
}

思路三

和思路二类似，形式上更容易理解

我们认为最下面的空指针null为第0层，往上走每层加一

因此，我们只需要统计左子树的高度和右子树高度中的较大值，然后再加1即可得到当前节点的高度

方法三完整代码

public int TreeDepth(TreeNode root) {
    if (root == null){
        return 0;
    }
    return Math.max(TreeDepth(root.left), TreeDepth(root.right)) + 1;
}