与普通的傅立叶变换,即 1 阶的分数阶傅立叶变换不同,分数阶傅立叶变换(p ≠ 1)提取的特征同时结合了原始图像的空间和频率特性。
分数傅里叶变换图像是介于原始图像和全傅里叶变换图像之间的东西。
Vander Lugt 相关器可以根据傅里叶变换后的频率信息进行二维相关和移不变滤波 。
移动不变性对于目标定位和跟踪是有用的,但对于许多图像的分类和关联可能会有太大的限制。具有轻微局部移位不变性的位置相关分类通常是足够的,也是首选的。
移位不变相关可以理解为具有Toeplitz互连矩阵的前馈神经网络的特征,该互连矩阵为移位不变共享适当的互连权重。
然而,这种权重分配大大降低了网络复杂度,导致存储容量有限,并且不适用于许多模式的分类。 取而代之的是,神经网络模型结合局部共享互连来提供具有良好分类性能的局部移位不变性。
论文扩展了 Vander Lugt 相关器,将基于两个分数阶傅立叶变换的移不变(频率)和位置相关滤波结合起来。由于分数阶傅里叶变换的光学结构简单,使得神经网络易于大规模实现。
基于分数阶傅里叶变换的光学空频滤波器
p=1/n 阶的分数傅立叶变换在连续应用 n 次时,由于其可加性,等效于执行一次普通傅立叶变换。
在分数阶傅里叶变换中,这种移位不变性在某种程度上被破坏,而与位置相关的信息被保持。 空间与频率相关信息的比值由阶数 p 控制。
当输入图像在4-f Vander Lugt 滤波器中的傅里叶平面滤波时,只执行频率滤波,导致卷积/相关积分。 尽管这种空间不变的输入到输出映射对于许多应用如目标定位和跟踪是有用的,但许多分类和联想记忆应用需要位置相关的映射,并且具有轻微的局部移位不变性。
论文将 4-f Vander Lugt 滤波器中的普通Fourier变换替换为阶数为 P1 和 P2 的分数阶Fourier变换。
分数阶傅立叶变换的显示积分公式为:

在这篇论文中,抑制了积分的无限域,

在这个近似范围内,PI和P2滤波器的输入输出映射关系现在为:
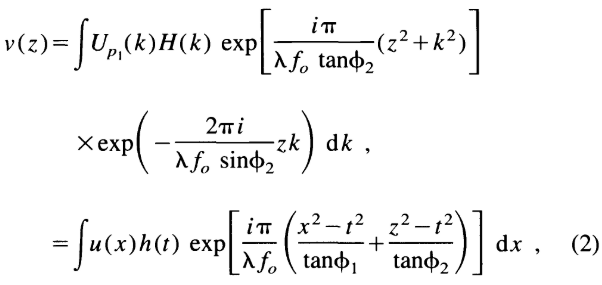
在上述公式(2)中,

如果 和
对于Vander Lugt滤波器都是1,
,
![]() ,
,,
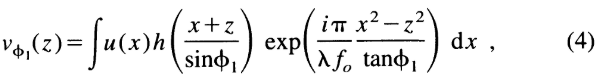
公式(4)中,

这种比例因子和指数调制项破坏了平移不变性,并提供了具有轻微局部平移不变性的位置相关分类。
移不变(频率)滤波和位置相关分类的相对重要性由![]() 控制。
控制。
基于分数阶傅立叶变换的神经网络


对于对称实函数H(x),它的分数傅里叶变换H(k)也变成复变函数。
提出的神经网络学习算法同样适用于滤波器的设计。 其光学结构类似于4-Fvander Lugt 滤波器,滤波器只需要两个透镜,而采用反向传播学习规则的单层自适应神经网络只需要三个透镜。 对多层神经网络的扩展是直接的,误差反向传播算法和光学结构仍然有效。


![[oeasy]python0048_注释_comment_设置默认编码格式](https://img-blog.csdnimg.cn/img_convert/0dbeb554a0180969f21851440d52e6ff.png)








![[230506] 2021年托福阅读真题第6篇|Water and Life on Mars|15:30~16:30|16:30~19:19](https://img-blog.csdnimg.cn/61623fe9e3624e30938fc8758f415e18.png)