《编程思维与实践》1042.字串变换

题目

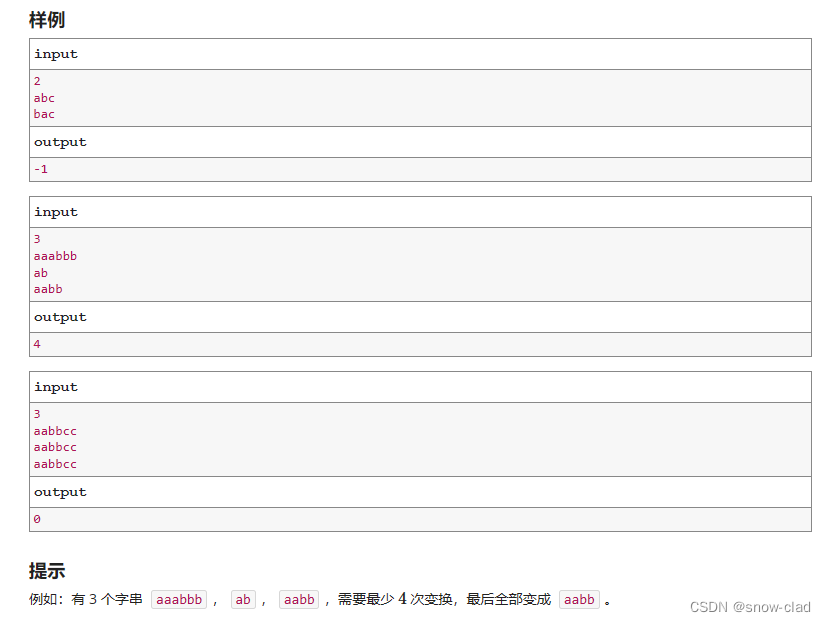
思路

分两步解决：

1.判断是否可以通过两种变换使所有的字符串变得相同；

2.在能变换的前提下使变换的次数最少。

其中第一步可以将每个字符串的基底(将连续重复出现的字符视为一个字符)求出来,

如: aaabbb的基底就是ab,进而只需判断基底是否相同即可;

第二步考虑贪心算法,只需要将每个基底变为相同实际字符数的变换次数最少即可,转化为数学语言也就是

如果一个字符a出现的次数分别为 $x_1,x_2...x_n$ , 需求出$i\in 1,\mathrm{2...}n$ , 使得$(|x_i-x_1|+...+|x_i-x_n|{)}_{min}$ ,

只需要找到$x_1,x_2...x_n$的中位数即可,将每一步与中位数作差取绝对值,即可求出变换的最少次数.

下面为可行性的说明:

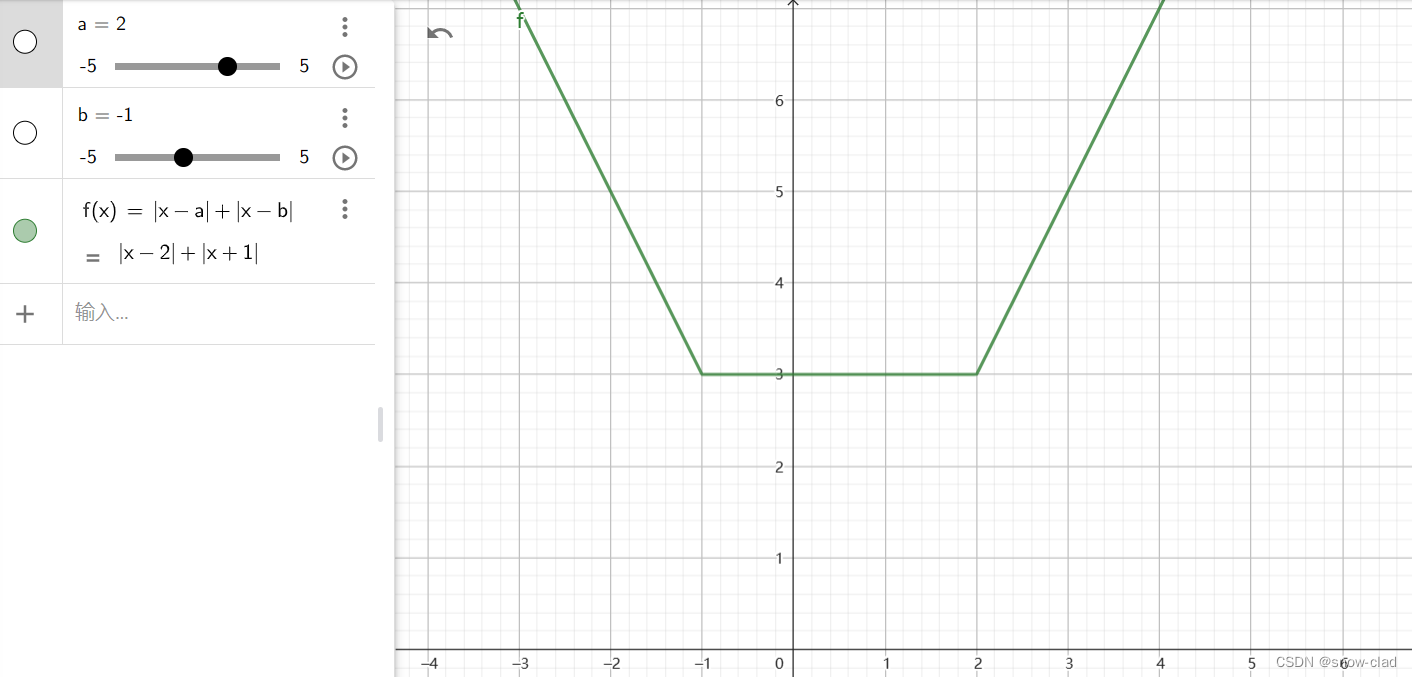
当 $n=2$ 时函数图像为:

此时函数在[a,b]中取最小值,特别地,如果函数是离散的,那么在中位数处取最小值;

当$n=3$时函数图像为:

此时函数在a,b,c的中位数处取最小值;

更一般的证明:
$$\begin{gathered} 将x_1,x_2...x_n升序排列,即x_1<x_2<..<x_n, \\ 当n为偶数时(n=2k):\sum _{i=1}^{2k}|x-x_i|=\sum _{i=1}^k(|x-x_i|+|x-x_{2k+1-i}|)\ge \sum _{i=1}^k(x_{2k+1-i}-x_i) \\ 当x\in [x,x_{2k+1-i}],\forall i\in 1,\mathrm{2...}k时上述等号成立, \\ 故当函数连续时,在中位数之间取最小值,函数离散时,在中位数(有两个中位数)处取最小值; \\ 当n为奇数时(n=2k+1):\sum _{i=1}^{2k+1}|x-x_i|=|x-x_{k+1}|+\sum _{i=1}^k(|x-x_i|+|x-x_{2k+2-i}|) \\ \ge |x-x_{k+1}|+\sum _{i=1}^k(x_{2k+2-i}-x_i) \\ 当x\in [x,x_{2k+2-i}],\forall i\in 1,\mathrm{2...}k时上述等号成立, \\ \ge \sum _{i=1}^k(x_{2k+2-i}-x_i)当且仅当x=x_{k+1}时成立. \\ 所以无论函数离散或者连续,都是在中位数处取最小值. \end{gathered}$$

注意的点:

1.以aaabbc 为例:先存a然后找到第一个与a不同的字符,这里采用后一个与前一个比较的方式(前一个与后一个比较也可以,稍微更换一下处理方式即可).

2.由于 $n<10^5$ 且字符长度不超过100所以变换数最多不超过$10^7$,用int存即可.

3.绝对值函数abs针对int类型,llabs针对long long 类型(整数绝对值在stdlib.h头文件),fabs针对double类型(浮点数在math.h头文件).

代码

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

typedef struct{char a[100];int count[100];}Data;  //a存基底 count存实际连续相同字符个数

int cmp(const void *a,const void *b)  //升序
{
	int *m=(int*)a;
	int *n=(int*)b;
	return *m-*n;
}

int main()
{
	int n;
	scanf("%d",&n);
	int sum=0;    //统计总次数
	Data tab[n+1];    //最后一组存中位数   
	for(int i=0;i<n+1;i++)
	{
		for(int j=0;j<100;j++)
		{
			tab[i].count[j]=0;
		}
	}
	
	for(int i=0;i<n;i++)
	{
		char s[101];
		scanf("%s",s);
		int j=0;
		for(int k=0;k<strlen(s);k++)
		{
            tab[i].a[j]=s[k];
            tab[i].count[j]++;
            while(s[k+1]==s[k])  //后一个与前一个相同
            {
                tab[i].count[j]++;
                k++;
            } 
            j++;
		}	
		tab[i].a[j]='\0';
	} 
	
	int flag=0;   //判断基底是否相同 
	for(int i=0;i<n-1;i++)
	{
		if(strcmp(tab[i].a,tab[i+1].a)) //不为0表示基底不同
		{
			flag=1;
			break;
		}
	}
	if(flag)
	{
		printf("-1\n");
	}
	else
	{
		int temp[n];   //找中位数
		for(int j=0;j<100;j++)   //遍历每个基底的实际连续字符数
		{
			for(int i=0;i<n;i++)
			{
				temp[i]=tab[i].count[j];
			}
			qsort(temp,n,sizeof(int),cmp);  
			tab[n].count[j]=temp[n/2];  //升序后找到中位数存在最后一组里
		}
		
		for(int i=0;i<n;i++)
		{
			for(int j=0;j<100;j++)
			{
				sum+=abs(tab[i].count[j]-tab[n].count[j]);  //与最后一组作差取绝对值
			}
		} 
		printf("%d\n",sum);
	}
	return 0;
}