加密的语法由三个算法组成:密钥产生,加密,解密
(1) 密钥产生算法Gen是一个概率算法,能够根据方案定义的某种分布方案分布选择并输出一个密钥k
(2) 加密算法Enc,输入为密钥k和明文m,输出为密文c。把使用密钥k加密明文m记为Enck(m) (Encryption)
(3)解密算法Dec,输入为密钥k和密文c,输出为明文m。把使用密钥k解密密文记为Deck(c) (Decryption)
用左箭头表示即使在同一组输入上运行两次,算法的输出也可能不同,
eg:,表示加密可能是随机的,同一组数据分别加密两次得到的密文也可能不同
用:=表示结果是确定性的
eg: m:=Deck(c),表示密文c通过密钥k可以得到唯一的一个结果
对任意加密方案的基本要求是:对于任何通过Gen输出的密钥k,每个明文消息,满足
Deck(Enck(m))=m
Kerckhoffs原则:加密算法应该公开


攻击场景:

mod 表示取余数,下图中第一个式子表明25%10与35%10具有相同的余数,第三个式子表明5等于35%10的结果

为了保证安全,必须有一个足够大的密钥空间防止暴力穷举搜索攻击。但足够大的密钥空间只是必要条件而非充分条件,不能保证方案是安全的
文中介绍了单字母替换,即每个明文字符映射到一个不同的密文字符,其中这种方法可以被英文文本中的字母平均概率猜测映射关系而攻破,但需要查看哪个明文结果是有意义的
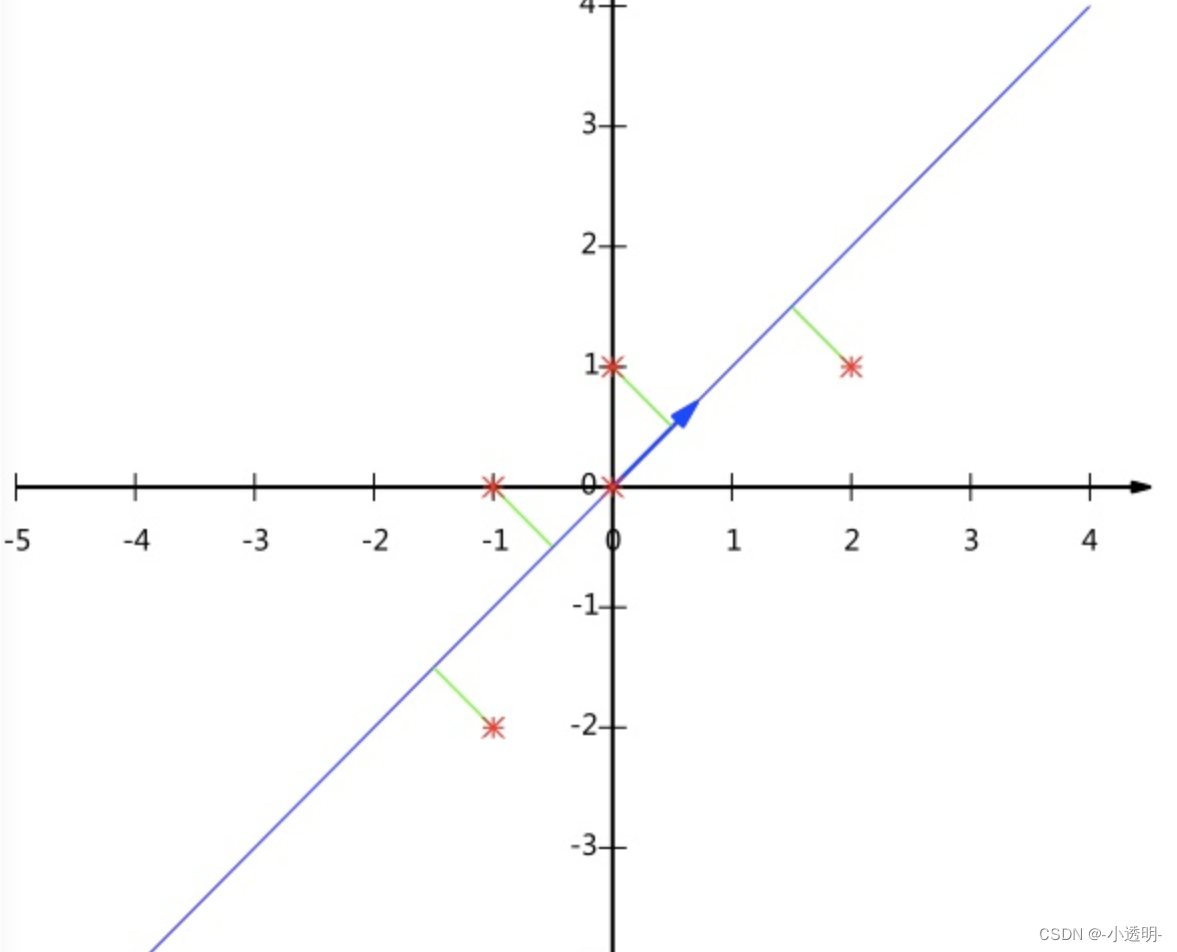
书中先利用图1.2算出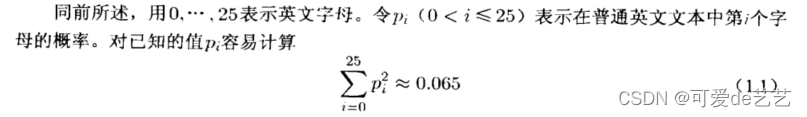
#include<bits/stdc++.h>
using namespace std;
int main()
{
double a[26];
double sum=0;
a[0]=0.082;
a[1]=0.015;
a[2]=0.028;
a[3]=0.042;
a[4]=0.127;
a[5]=0.022;
a[6]=0.02;
a[7]=0.061;
a[8]=0.001;
a[9]=0.008;
a[10]=0.04;
a[11]=0.024;
a[12]=0.067;
a[13]=0.075;
a[14]=0.019;
a[15]=0.001;
a[16]=0.06;
a[17]=0.063;
a[18]=0.09;
a[19]=0.028;
a[20]=0.01;
a[21]=0.024;
a[22]=0.02;
a[23]=0.001;
a[24]=0.001;
a[25]=0.07;
for(int i=0;i<26;i++)
{
sum=sum+a[i]*a[i];
}
cout<<sum;//结果为0.065379
}
解释:对于每个i,他移位后的位置记作i+k(用来代替取余数运算),如果猜测得出的位置i+j与i+k相同,此时在密文中得出的频率q(i+j)应与pi相近,此时求出的j即为可能的偏移量。根据式1.1,同时按照上图所计算的式子,若Ij≈0.065,则可能是一组key值
Vigenere加密:



解释:假设密钥的长度为t,则密文可以被分为t个部分,每一个部分中移位的量都是一致的。在每个部分中利用概率制表,他们仍符合图1.2,同样可以利用式
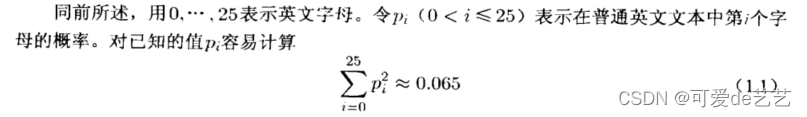
计算t次即可算出密钥