从0开始的秋招刷题路,记录下所刷每道题的题解,帮助自己回顾总结
902. 最大为 N 的数字组合
给定一个按 非递减顺序 排列的数字数组 digits 。你可以用任意次数 digits[i] 来写的数字。例如,如果 digits = [‘1’,‘3’,‘5’],我们可以写数字,如 ‘13’, ‘551’, 和 ‘1351315’。
返回 可以生成的小于或等于给定整数 n 的正整数的个数 。
示例 1:
输入:digits = [“1”,“3”,“5”,“7”], n = 100
输出:20
解释:
可写出的 20 个数字是:
1, 3, 5, 7, 11, 13, 15, 17, 31, 33, 35, 37, 51, 53, 55, 57, 71, 73, 75, 77.
示例 2:
输入:digits = [“1”,“4”,“9”], n = 1000000000
输出:29523
解释:
我们可以写 3 个一位数字,9 个两位数字,27 个三位数字,
81 个四位数字,243 个五位数字,729 个六位数字,
2187 个七位数字,6561 个八位数字和 19683 个九位数字。
总共,可以使用D中的数字写出 29523 个整数。
示例 3:
输入:digits = [“7”], n = 8
输出:1
提示:
1 <= digits.length <= 9
digits[i].length == 1
digits[i] 是从 ‘1’ 到 ‘9’ 的数
digits 中的所有值都 不同
digits 按 非递减顺序 排列
1 <= n <=
1
0
9
10^9
109
解题思路
一眼看过去,数学题,排列组合嘛。
老样子先自己构造两个测试数据: D = [“3”,“4”,“6”,“7”] N = 75134

很显然,对于一个 5 位数的 N 来说,所有 4/3/2/1 位数的数字都一定小于它
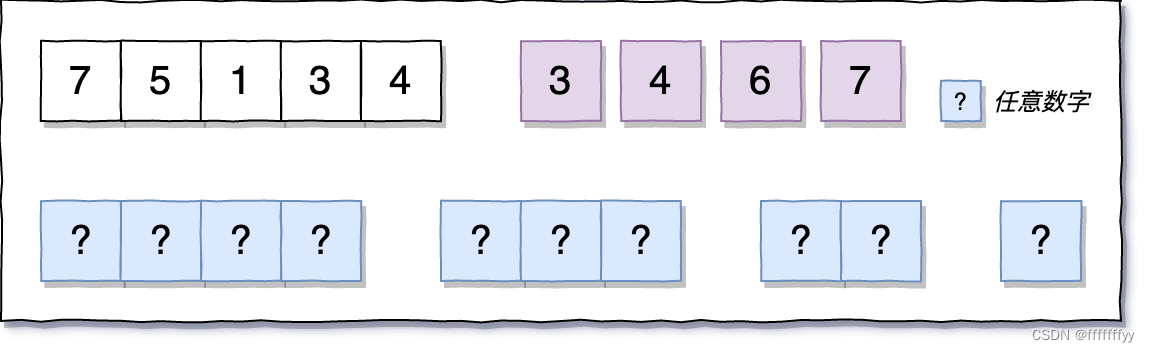
这也是最好计算的部分,每一位都有 4 个数字可以选择,也就是分别有 4⁴ , 4³ , 4² , 4¹ 种情况。
而 5 位数的情况,就相对复杂了许多,需要多考虑点了:
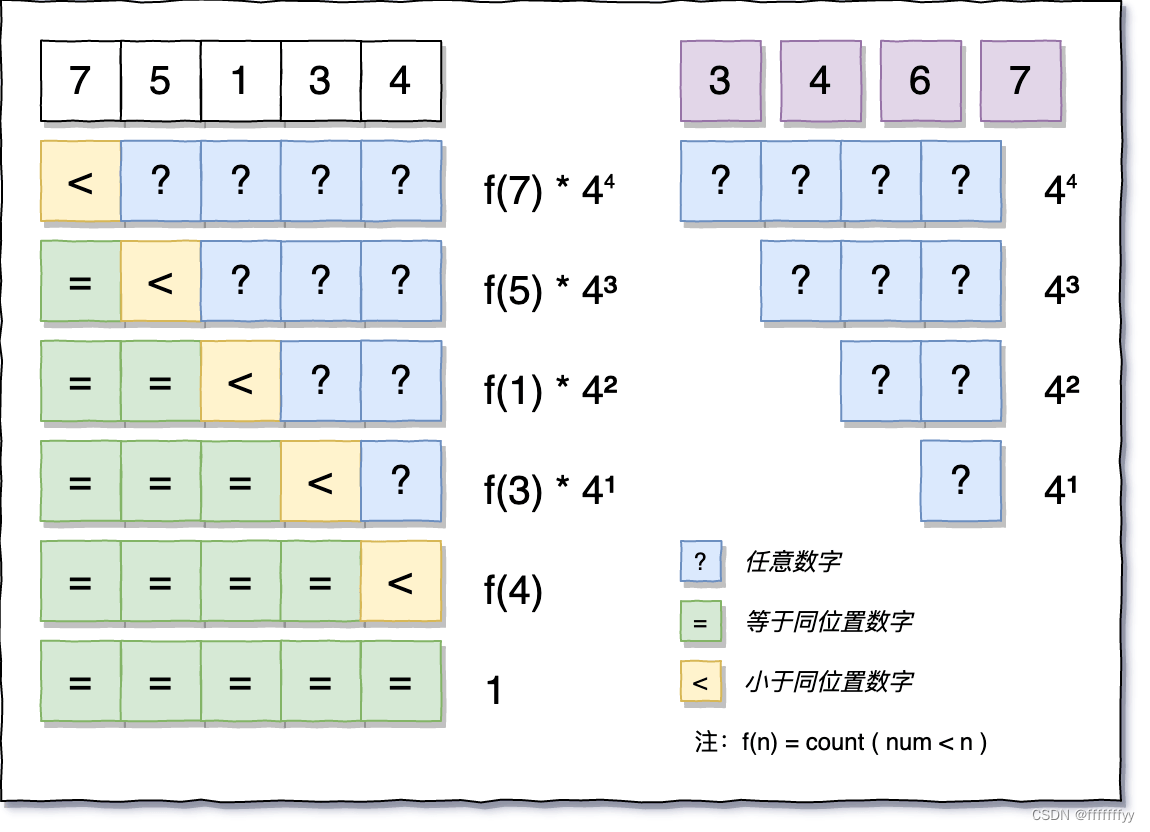
如上图所示,5 位数的话,假如第一位比 7 小,那么后面四位其实就没所谓大小了。
此时组合的数量就是 第一位的情况数量 f(7) * 4⁴,后四位的情况,恰好对应了只有四位数的时候。
但是如果第一位恰好等于 7 呢?那就只能要求第二位小于 5 了,最后那三位可以随意。
以此类推,直到五位数每一位都等于相应的数字,那就只有一种情况了。
图中在每一种组合后面,标注了相应的数量。
但是,仔细观察一下我们提供的数组 D ,里面压根没有 5, 1这两个数字啊:
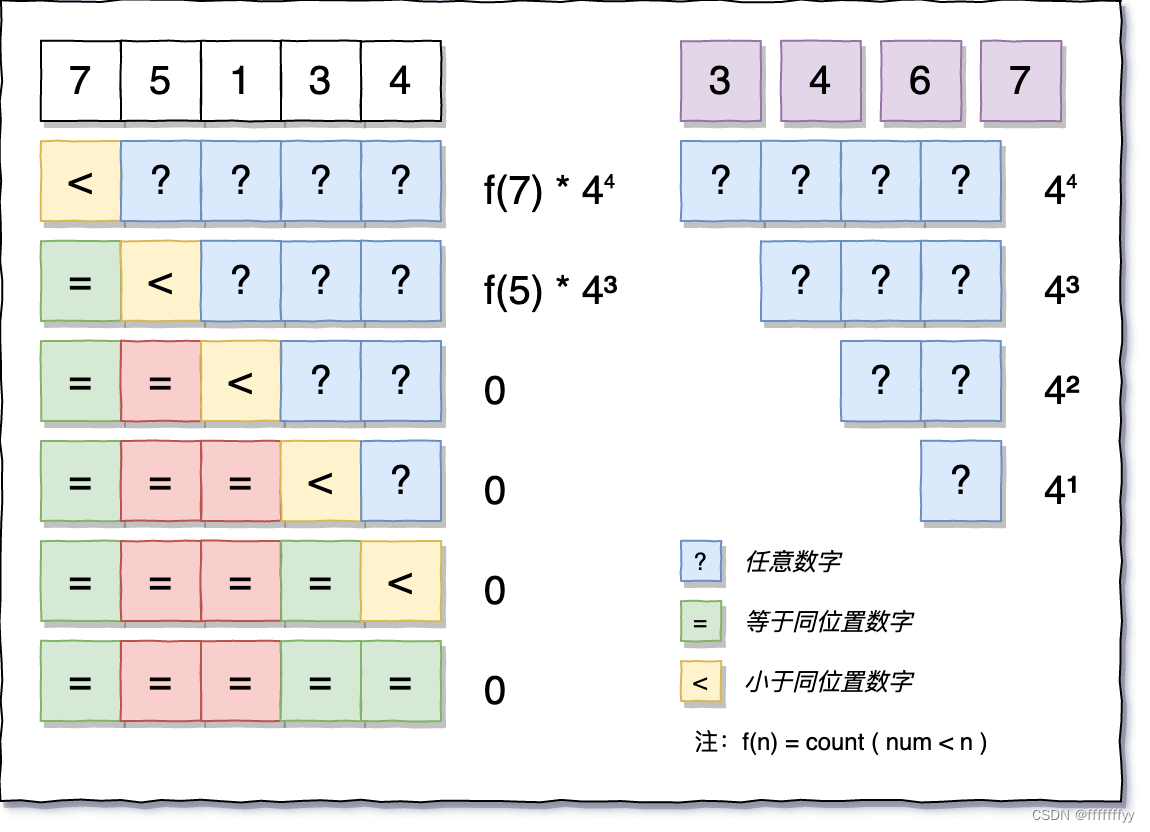
如上图所示,红色表示并不存在的数字,可以看到由于 5的影响,其实后面的几种情况已经全都不用计算了,压根不会出现。
那么思路就已经比较清晰了,和目标数字相等长度的数字需要遍历查找,其它数字可以直接计算得出来。
代码
class Solution {
public int atMostNGivenDigitSet(String[] D, int N) {
int ans = 0;
// 对 D 数组进行预处理
int[] less_than_d = new int[10];
int[] d_arr = new int[10];
for (int i = 0; i < D.length; i++) {
Arrays.fill(less_than_d, Integer.parseInt(D[i]) + 1, 10, i + 1);
d_arr[Integer.parseInt(D[i])] = 1;
}
// 一位数的 N 可以直接返回
if (N / 10 == 0)
return less_than_d[N] + d_arr[N];
// 将 N 打平存入数组
int n_len = 0;
int[] n_arr = new int[10];
while (N != 0) {
n_arr[n_len] = N % 10;
n_len += 1;
N = N / 10;
}
// 把各种幂算出来备用,n_pow[2] 里存的是平方
int[] n_pow = new int[n_len];
n_pow[0] = 1;
for (int i = 1; i < n_len; i++)
ans += (n_pow[i] = D.length * n_pow[i - 1]);
// 将所有可能性加起来
ans += less_than_d[n_arr[n_len - 1]] * n_pow[n_len - 1];
for (int i = n_len - 1; i >= 0; i--)
if (d_arr[n_arr[i]] == 1)
ans = i == 0 ? ans + 1 : ans + less_than_d[n_arr[i - 1]] * n_pow[i - 1];
else
break;
return ans;
}
}