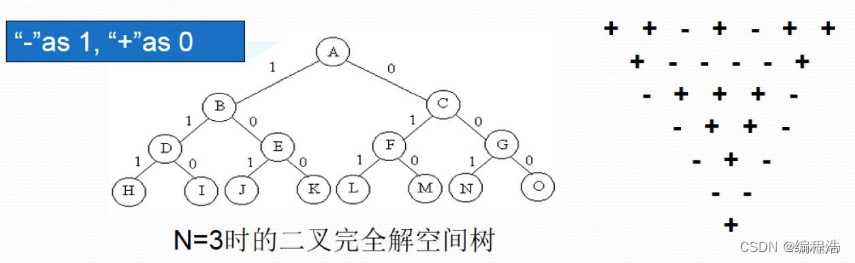
下图是由14个“+”和14个“-”组成的符号三角形。2个同号下面都是“+”，2个异号下面都是“-”。

在一般情况下，符号三角形的第一行有n个符号。符号三角形问题要求对于给定的n，计算有多少个不同的符号三角形，使其所含的“+”和“-”的个数相同。

题意分析

也就是 给了一个n数字

然后就会形成 第一行长度为n的三角形

然后用+ -号 把三角形填充

问是否可以用 + -号相等的数量 进行填充三角形

可以有多少中方案？？？

思路过程分析

首先我们利用简单的样例分析
如果n=3
然后我们用一行为
+++分析 如果第一行是+++，根据+和-个数相等，剩下的符合只能是—

所以如下
+++
- -
-

如果是

+-+
--
+

++-
-+
-

由上总结出规律就是，如果第一行确定了，那么剩下的行都是根据上一行而确定的

也就是

+++  第一行都是+
第二行 就上 它的左上角和右上角
++ 得-
+- 得+
-+ 得+
-- 得+

根据这个规律就能构图了

所以我们那就先把第一行的所有情况都遍历一边，
然后把每次情况都构图一次，
记录下+ -号的个数
看 + -号是不是各一半

算法分析

我们已经知道 过程了

那么如何 写出算法？

首先由于 要把第一行的所有情况都遍历一边

那么我们就是要用 dfs全排列方法遍历

所以我们用dfs（t）t表示第一行中的位置
构建第一行，

但是我们发现，比如n = 100，t = 20时候，其实是可以把前20个所对应下面的行构建出来，并且如果这种情况下，如果-号或者+号已经大于一半，那么就不可能是这种情况了，就直接剪纸了

比如 n = 3
++未知
-未知
未知

也就是如果知道前两个是++
那么第二行的第一个也就知道了

这样的算法就可以是优化后的算法了

本题的思路 也就差不多了
直接上代码

//5-4 符号三角形问题
//0+  1-
#include <iostream>
using namespace std;
int n;//n行，第一行有n个元素 
int sum=0;//记录满足题意的数
int half;//n*(n+1)/4 
int cnt;//'-'的个数
int p[100][100]; //符号三角形矩阵 
void Output(){
	cout<<"------------\n";
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n-i+1;j++){
			cout<<p[i][j]<<" ";
		}
		cout<<endl;
	}
} 
void BackTrack(int t){ //第t行 
//	cout<<"cnt="<<cnt<<" half="<<half<<endl;
	//正负号如果出现 一方>half
	if(cnt>half || (t*(t-1)/2-cnt)>half) return;
	if(t>n){
		Output(); 
		sum++;	
	}
	else{
		for(int i=0;i<=1;i++){
			p[1][t] = i;
			cnt += i;//'-'的个数
			for(int j=2;j<=t;j++){
				p[j][t-j+1] = p[j-1][t-j+1] ^ p[j-1][t-j+2];//^相同取0，不同取1 
				cnt+=p[j][t-j+1];
			}
			BackTrack(t+1);
			for(int j=2;j<=t;j++){
				cnt-=p[j][t-j+1];
			} 
			cnt -= i;
		}
	}
} 
int main(){
	cin>>n;
	half=n*(n+1)/2;//共有n*(n+1)/2个符号 
	
	if(half%2==1){  //奇数个符号的话，不存在'+'的个数等于'-'的个数 
		cout<<"无解\n";
	}
	else{
		half=half/2;
		BackTrack(1);
		cout<<"sum="<<sum<<endl;
	}

	return 0;
} 
/*
7
*/