【LetMeFly】2106.摘水果

力扣题目链接：https://leetcode.cn/problems/maximum-fruits-harvested-after-at-most-k-steps/

在一个无限的 x 坐标轴上，有许多水果分布在其中某些位置。给你一个二维整数数组 fruits ，其中 fruits[i] = [position_i, amount_i] 表示共有 amount_i 个水果放置在 position_i 上。fruits 已经按 position_i 升序排列 ，每个 position_i 互不相同 。

另给你两个整数 startPos 和 k 。最初，你位于 startPos 。从任何位置，你可以选择 向左或者向右 走。在 x 轴上每移动 一个单位 ，就记作一步。你总共可以走最多 k 步。你每达到一个位置，都会摘掉全部的水果，水果也将从该位置消失（不会再生）。

返回你可以摘到水果的 最大总数 。

示例 1：

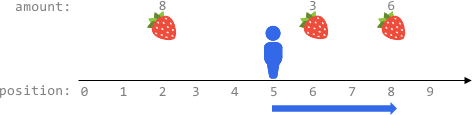
输入：fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4
输出：9
解释：
最佳路线为：
- 向右移动到位置 6 ，摘到 3 个水果
- 向右移动到位置 8 ，摘到 6 个水果
移动 3 步，共摘到 3 + 6 = 9 个水果

示例 2：

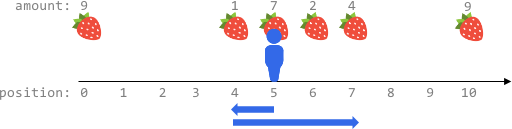
输入：fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4
输出：14
解释：
可以移动最多 k = 4 步，所以无法到达位置 0 和位置 10 。
最佳路线为：
- 在初始位置 5 ，摘到 7 个水果
- 向左移动到位置 4 ，摘到 1 个水果
- 向右移动到位置 6 ，摘到 2 个水果
- 向右移动到位置 7 ，摘到 4 个水果
移动 1 + 3 = 4 步，共摘到 7 + 1 + 2 + 4 = 14 个水果

示例 3：

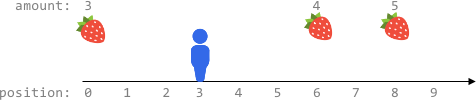
输入：fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2
输出：0
解释：
最多可以移动 k = 2 步，无法到达任一有水果的地方

提示：

1 <= fruits.length <= 10⁵
fruits[i].length == 2
0 <= startPos, position_i <= 2 * 10⁵
对于任意 i > 0 ，position_i-1 < position_i 均成立（下标从 0 开始计数）
1 <= amount_i <= 10⁴
0 <= k <= 2 * 10⁵

方法一：滑动窗口

滑动窗口的核心思路是：使用两个指针l和r指向fruits数组，l和r之间的部分称为“窗口”。每次右指针r右移一位，左指针移动到“满足题目条件”且尽可能靠左的位置。

什么叫“满足题目条件”？“满足题目条件”是指从startPos左右移动k步内能经过l和r。

这样，右指针每次只移动一位，左指针也是在上次的位置基础上进行移动的（总计移动次数不超过数组长度），因此窗口移动的总时间复杂度是 $O (l e n (f r u i t s))$

所以，我们只需要编写一个函数：minStep，来计算从startPos处开始左右移动，经过l和r，至少需要几步。

如果fruits[r]的位置小于startPos，就说明窗口完全位于起点左边，只需要从起点移动到l处即可（ $s t a r tP os - f r u i t s [l] [0]$ ）
如果fruits[l]的位置大于startPos，就说明窗口完全位于起点右边，只需要从起点移动到r处即可（ $f r u i t s [r] [0] - s t a r tP os$ ）
否则，说明窗口横跨起点，需要从起点移动到l再返回并移动到r，或者从起点移动到r再返回移动到l（ $\min(2\times 起点到l + 起点到r, 起点到l + 2\times 起点到r)$ ）

对于窗口l到r，调用这个函数就能很轻松地计算出当前窗口能否在k步之内被覆盖

时间复杂度 $O (l e n (f r u i t s))$
空间复杂度 $O (1)$

AC代码

C++

class Solution {
private:
    int minStep(vector<vector<int>>& fruits, int l, int r, int startPos) {
        if (fruits[r][0] <= startPos) {  // 全在起点左边
            return startPos - fruits[l][0];
        }
        else if (fruits[l][0] >= startPos) {  // 全在起点右边
            return fruits[r][0] - startPos;
        }
        else {  // 横跨起点左右
            int leftDistance = startPos - fruits[l][0];
            int rightDistance = fruits[r][0] - startPos;
            return min(2 * leftDistance + rightDistance, leftDistance + 2 * rightDistance);
        }
    }
public:
    int maxTotalFruits(vector<vector<int>>& fruits, int startPos, int k) {
        int ans = 0;
        int cnt = 0;  // 窗口中的水果总数
        int l = 0;
        for (int r = 0; r < fruits.size(); r++) {
            cnt += fruits[r][1];
            while (l <= r && minStep(fruits, l, r, startPos) > k) {
                cnt -= fruits[l][1];
                l++;
            }
            ans = max(ans, cnt);
        }
        return ans;
    }
};

Python

# from typing import List

class Solution:
    def minStep(self, fruits: List[List[int]], startPos: int, l: int, r: int) -> int:
        if fruits[r][0] <= startPos:
            return startPos - fruits[l][0]
        elif fruits[l][0] >= startPos:
            return fruits[r][0] - startPos
        else:
            leftDistance = startPos - fruits[l][0]
            rightDistance = fruits[r][0] - startPos
            return min(2 * leftDistance + rightDistance, leftDistance + 2 * rightDistance)
    
    def maxTotalFruits(self, fruits: List[List[int]], startPos: int, k: int) -> int:
        ans = 0
        cnt = 0
        l = 0
        r = 0
        while r < len(fruits):
            cnt += fruits[r][1]
            while l <= r and self.minStep(fruits, startPos, l, r) > k:
                cnt -= fruits[l][1]
                l += 1
            ans = max(ans, cnt)
            r += 1
        return ans