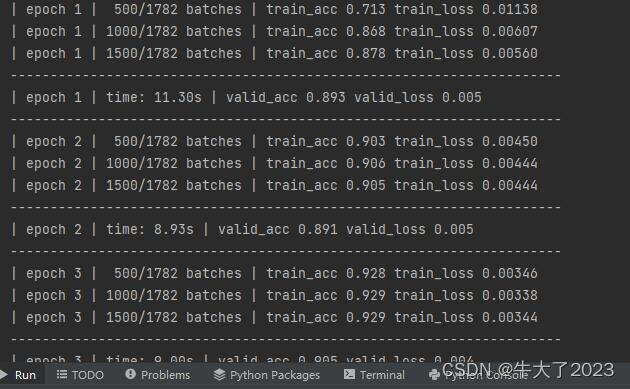
文章目录
- 基本概念
- n阶B树的性质(n>=2)
- B树的搜索
- B树元素的添加
- 上溢出解决
- 删除
- 删除叶子节点
- 删除非叶子节点
- 删除——导致下溢出
- 删除——解决下溢出方法一
- 删除——解决下溢出方法二
- MongoDB
基本概念
B树是为磁盘或其他直接存取的辅助存储设备而设计的一种平衡搜索树。
B树类似于红黑树,但它们在降低磁盘 I/O 操作数方面要更好一些。
许多数据库系统使用 B树或者 B树的变种来存储信息。
B树与红黑树的不同之处在于 B树的结点可以有很多孩子,从数个到数千个。也就是说,一个 B树的“分支因子”可以相当大,尽管它通常依赖于所使用的磁盘单元的特性。
B树类似于红黑树,就是每棵含有n个结点的 B树的高度为 O(lgn)。然而,一棵 B树的严格高度可能比一棵红黑树的高度要小许多,这是因为它的分支因子,也就是表示高度的对数的底数可以非常大。因此,我们也可以使用 B树在时间 O(lgn)内完成一些动态集合的操作。
3阶B树:子节点最多为3个
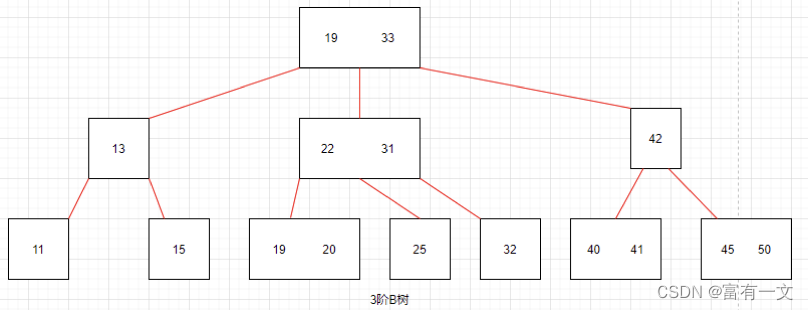
4阶B树:子节点最多为4个

n阶B树的性质(n>=2)
假设一个节点存储的元素个数为x,则
1、根节点:1<=x<=n-1
2、非根节点:ceil(n/2)-1<= x<= n-1 (ceil向上取整)
如果有子节点,子节点个数y=x+1,则
1、根节点: 2<=y<=n
2、非根节点:ceil(n/2) <= y<= n
比如n=3,2<= y <=3,因此可以称为(2,3)树、2-3树
比如n=4,2<= y <=4,因此可以称为(2,4)树、2-3-4树
比如n=5,3<= y <=5,因此可以称为(3,5)树
比如n=6,3<= y <=6,因此可以称为(3,6)树
比如n=7,4<= y <=7,因此可以称为(4,7)树
B树的搜索
B树的搜索跟二又搜索树的搜索类似,只不过分叉比二又搜索树更多
1、先在节点内部从小到大开始查找元素
2、如果找到了,查找结束
3、如果没有找到,再到对应的子节点继续查找元素,重复步骤1
B树元素的添加
新添加的元素必定是添加到叶子节点。
原始树:

插入52:

插入101:

注意:假设再插入102,则最右边的叶子节点的元素个数将超过4阶B树的限制,这种现象我们称之为上溢出。
上溢出解决
n阶B树上溢节点的元素个数必然等于n。上溢的解决办法:
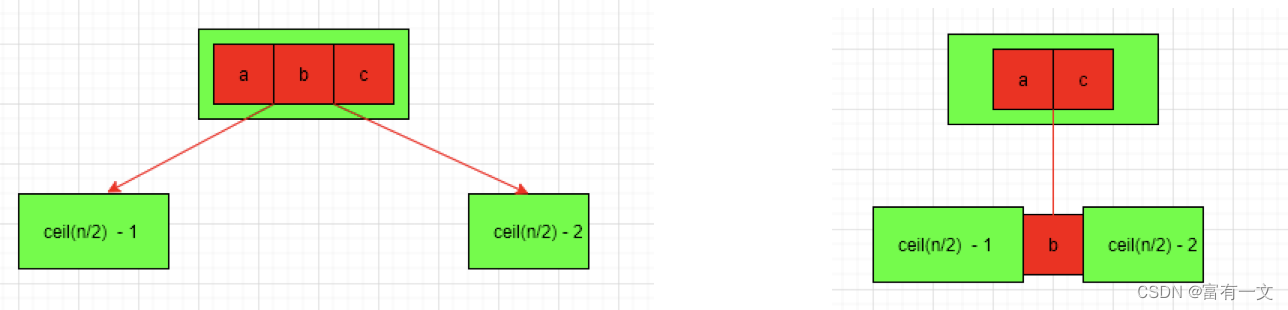
1、假设上溢节点最中间元素的位置为k,则可以:
a. 将k位置的元素向上与父节点合并
b. 将[Ok-1]和[k+1,n-1]位置的元素分裂成两个子节点,此时这两个子节点的元素个数,必然都不会低于最低限制(ceil(n/2)-1)
2、一次分裂完毕后,有可能导致父节点上溢,依然按照上述方法解决最极端的情况,有可能一直分裂到根节点。
如下图所示:

删除
删除叶子节点
如果需要删除的元素在叶子节点中,那么可以直接删除元素。

对上图删除56:

删除非叶子节点
假如需要删除的元素在非叶子节点中。
1、先找到前驱或者后继元素,用前驱或者后继元素的值覆盖需要删除元素的值
2、再把前驱或后继元素删除
删除19:

非叶子节点的前驱或后继元素,必定在叶子节点中
所以其实删除非叶子节点元素最终一定能转换成删除在叶子节点中的元素
删除——导致下溢出

一颗5阶B树,要删除元素28
叶子节点被删掉一个元素后,元素个数可能会低于最低限制(>=ceil(n/2)-1)
这种现象称为:下溢
删除——解决下溢出方法一
下溢节点的元素数量必然等于ceil(n/2)-2
如果下溢节点临近的兄弟节点,有至少ceil(n/2)个元素,可以向其借一个元素
1、将父节点的元素b插入到下溢节点的0位置最小位置)
2、用兄弟节点的元素a(最大的元素)替代父节点的元素b
这种操作其实就是:旋转

删除——解决下溢出方法二
如果下溢节点临近的兄弟节点,只有ceil(n/2)-1个元素
1、将父节点的元素b挪下来跟左右子节点进行合并
2、合并后的节点元素个数等于ceil(n/2) + ceil(n/2) – 2,不超过n-1
这个操作可能会导致父节点下溢,依然按照上述方法解决,下溢现象可能会一直往上传播
MongoDB
MongoDB就是使用的B树实现。
ps:计划每日更新一篇博客,今日2023-05-03,日更第十七天。
昨日更新:
剑指Offer II 052——展平二叉搜索树