扫地机器人

题目描述

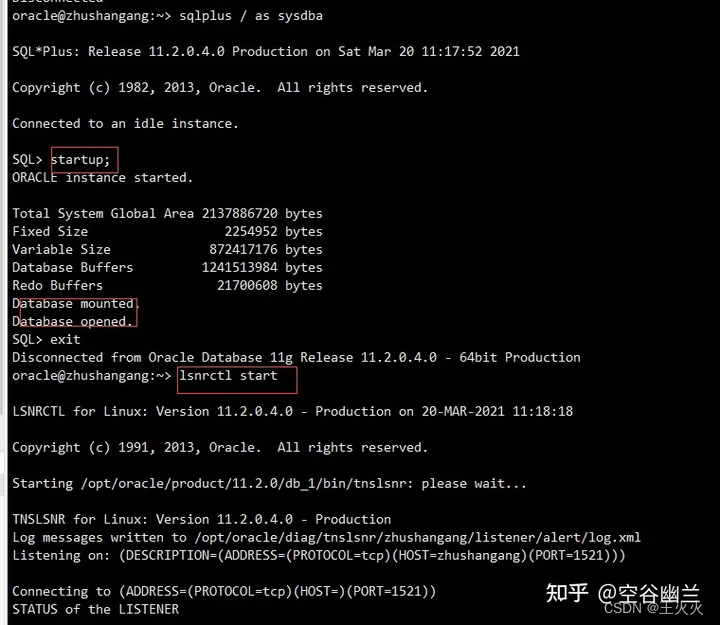
小明公司的办公区有一条长长的走廊，由 N 个方格区域组成，如下图所示。

走廊内部署了 K 台扫地机器人，其中第 i 台在第 A_i 个方格区域中。已知扫地机器人每分钟可以移动到左右相邻的方格中，并将该区域清扫干净。

请你编写一个程序，计算每台机器人的清扫路线，使得

1. 它们最终都返回出发方格，
2. 每个方格区域都至少被清扫一遍，
3. 从机器人开始行动到最后一台机器人归位花费的时间最少。

注意多台机器人可以同时清扫同一方块区域，它们不会互相影响。

输出最少花费的时间。 在上图所示的例子中，最少花费时间是 6。第一台路线：2-1-2-3-4-3-2，清 扫了 1、2、3、4 号区域。第二台路线 5-6-7-6-5，清扫了 5、6、7。第三台路线 10-9-8-9-10，清扫了 8、9 和 10。

输入描述

第一行包含两个整数 N,K。

接下来 KK 行，每行一个整数 A_i。

其中，$1\le K<N\le 10^5$，$1\le A_i\le N$。

输出描述

输出一个整数表示答案。

样例

#1

10 3
5
2
10

6

提示

解析

题目要求多个机器人一起扫地，需要最少多少时间可以全部扫完，根据贪心思想，既然我们有 K 台机器人，路程为 N，那么我们自然是要把路程均分给每台机器人才可以得到最少时间，每台机器人负责 N/K 区域。

题目还说机器人起点出发最终会回到起点，即 $a\to b、b\to c、c\to d$ 最终还得 $d\to c、c\to b、b\to a$ 回来，也就是说扫了 4 个距离，花费了 6 时间，不管从 $a、b、c、d$ 那个位置为起点，亦是如此，因此我们可以根据机器人扫的距离得到时间 $(距离-1)\times 2$ 。

给定一个每台机器人能扫的距离 m，校验每台机器人扫了 m 距离后，能否扫完整个路程，若可以则继续缩小 m ，否则扩大 m，从这里就能看得出来只是二分思想。

分析一下机器人扫地情况：

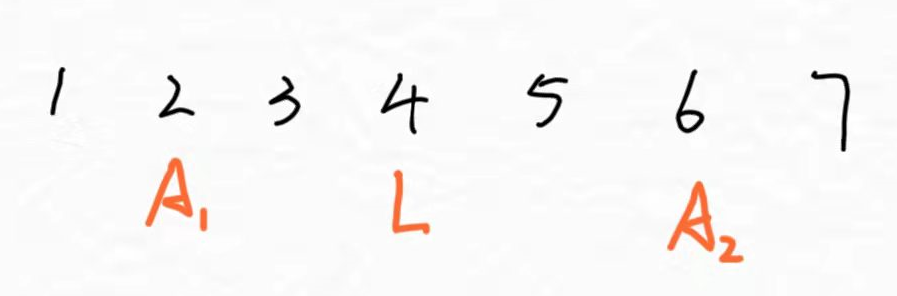
• $A_2$ 机器人可以扫到 L
• $A_1$ 机器人左边已经被扫过了，不用扫了

AC Code

public class Main {
	static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	static StreamTokenizer st = new StreamTokenizer(br);
	static PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));

	public static void main(String[] args) throws Exception {
		int n = nextInt(), m = nextInt();
		int[] A = new int[n + 1];
		for(int i = 1; i <= m; i++) A[i] = nextInt();
		Arrays.sort(A, 1, m + 1);
		int left = 0, right = n;
		int ans = 0;
		while(left <= right) {
			int mid = (left + right) >>> 1;
			if(check(A, mid, m, n)) {
				right = mid - 1;
				ans = mid;
			} else {
				left = mid + 1;
			}
		}
		System.out.println((ans - 1) * 2);
	}
	
	public static boolean check(int[] A, int p, int m, int n) {
		int L = 0; // 从左边开始，机器人已经扫完了 L 距离
		for(int i = 1; i <= m; i++) {
			if(A[i] - p <= L) { // 机器人 A[i] 可以扫到 L 
				if(A[i] <= L && A[i] + p > L) // 机器人 A[i] 左边已经被扫完了，不用扫了
                    L = A[i] + p - 1; 
				else L = L + p;
			} else { // 无法扫到 L
				return false;
			}
		}
		return L >= n; // 是否扫完
	}
	
	public static int nextInt() throws Exception {
		st.nextToken();
		return (int) st.nval;
	}
}