1.点乘:
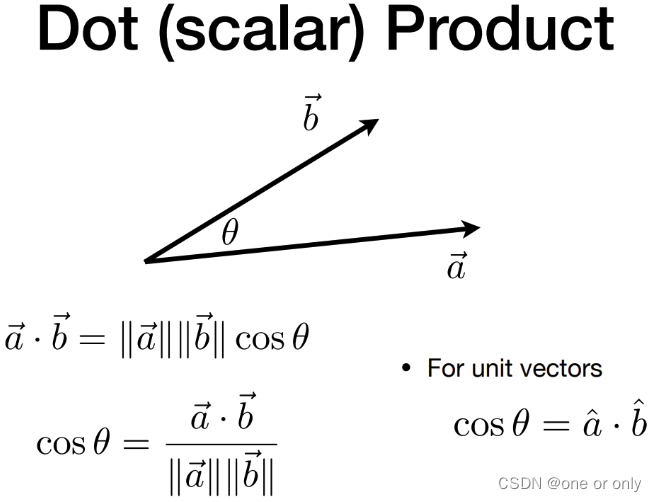
向量点乘 → 一个数值
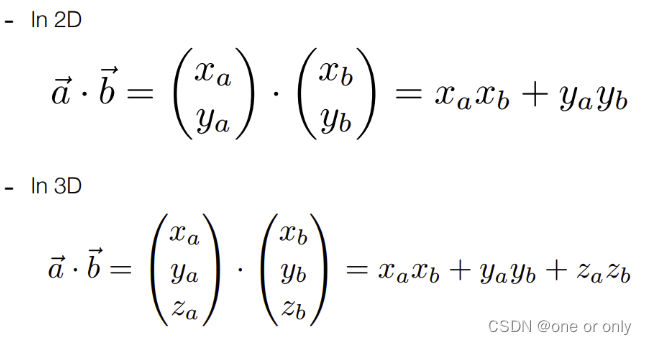
点乘在图形学中的应用:
- 找到两个方向之间的夹角。
- 找到一个向量投影到另一个向量上是什么样的。
- 计算两个向量的方向(是接近还是远离)判定高光范围,从1(重合) → 0(垂直)→ -1(完全远离)
- 关于前与后。


2.叉乘:
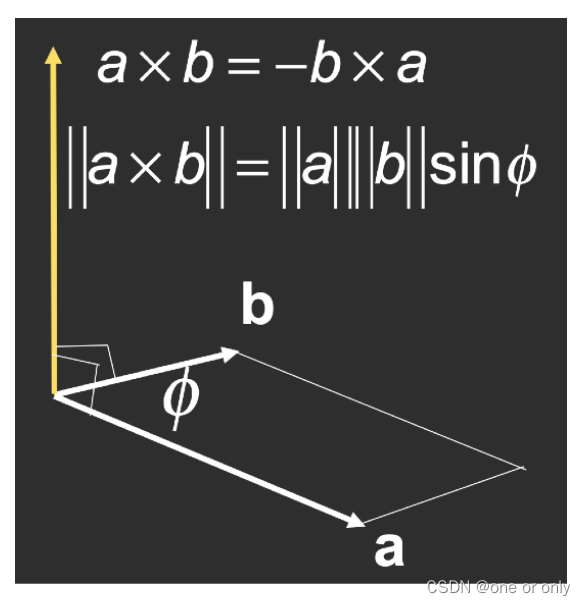
使用右手定则,x轴叉乘y轴得到z轴方向。(右手四指弯曲的方向由a指向b,大拇指的方向即为z轴的方向)
向量叉乘得到向量。
叉乘在图形学中的应用:
- 点在向量的左边,还是在向量的右边(根据右手螺旋规则:叉乘结果大于0,则P点在向量左侧;叉乘结果小于0,则P点在向量右侧;结果等于0,则P点在向量上);
- 点在三角形内,还是在三角形外(计算像素是否在三角形内容)。
基础的题!!!如何判断点在三角形内部

判定b在a左侧还是右侧(朝向屏幕外{其实对应坐标轴z轴的正方形},z轴是正数,所以大于0,在左侧)
- a叉乘b,结果>0,左侧。
- 结果<0,右侧。
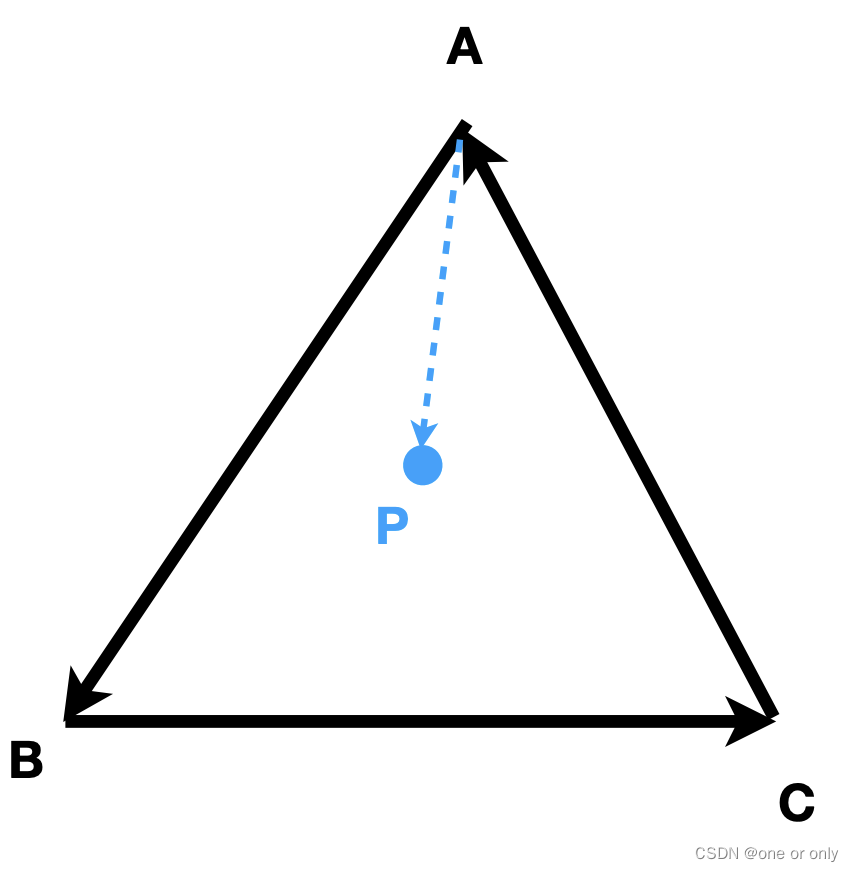
判定p点是否在三角形内部(向外朝向屏幕外,就是不指向屏幕)
- AB 叉乘 AP ,向外 — P在AB左侧
- BC 叉乘 BP,向外 — P在BC左侧
- CA 叉乘 CP,向外 — P在CA左侧
- 综合,P在三角形内部
只有全是左侧或者右侧才能判定点在三角形内侧
z轴朝向屏幕外是正方向,摄像机前向是z轴负方向