1. 原始HHO算法

详细介绍此处略，可参考HHO算法介绍

2. 改进的哈里斯鹰优化算法

2.1 动态自适应逃逸能量E

猎物逃逸能量E是HHO平衡全局探索与局部开发行为的重要参数。HHO中对猎物逃逸能量E的描述是由最大值线性递减至最小值，这种线性能量递减策略导致算法的探索和发开平衡性较差，且无法准确表征实际情况下鹰与猎物多轮围捕逃逸过程。 为此，在HHO能量递减策略中引入动态自适应权重。

2.2 拉普拉斯交叉算子

HHO算法在迭代后期种群多样性降低且对最优个体依赖性较大，当最优个体陷入局部最优后种群难以跳出局部极值空间。为此，采用拉普拉斯交叉算子策略对迭代后期种群内部适应度最高的两个个体进行交叉扰动，提高跳出局部最优的能力。

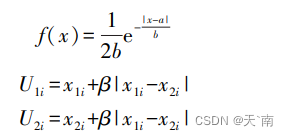
其中，$U_{1i}$和$U_{2i}$为拉普拉斯算子交叉后产生的子代个体的位置，$x_{1i}$和$x_{2i}$分别为解空间中适应度最高的两个个体的位置。

2.3 动态自适应权重

基本哈里斯鹰优化算法的更新阶段，在迭代初期的快速俯冲软围捕和硬围捕阶段就向全局最优解逼近，会导致搜索范围不足，陷入局部最优，使搜索失败。为克服这一弊端，再在其位置更新公式中加入动态权重系数 ω，让它在迭代初期具有较大值，促进全局搜索，迭代后期自适应变小，促进局部搜索并加快收敛速度。

3. 部分代码展示

clear
close all
clc

N=30; % Number of search agents
Function_name='F7'; % Name of the test function 
T=500; % Maximum number of iterations
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);

[Rabbit_Energy,Rabbit_Location,CNVG]=HHO(N,T,lb,ub,dim,fobj);
[Rabbit_Energy_IHHO,Rabbit_Location_IHHO,CNVG_IHHO]=IHHO(N,T,lb,ub,dim,fobj);

%Draw objective space
figure
semilogy(CNVG,'Color','b','LineWidth',2);
hold on 
semilogy(CNVG_IHHO,'Color','r','LineWidth',2);
title([num2str(Function_name), '的寻优曲线']);
xlabel('Iteration');
ylabel('Best fitness obtained so far');
legend('HHO','IHHO')
legend('HHO')

display(['The best location of HHO is: ', num2str(Rabbit_Location)]);
display(['The best fitness of HHO is: ', num2str(Rabbit_Energy)]);
display(['The best location of IHHO is: ', num2str(Rabbit_Location_IHHO)]);
display(['The best fitness of IHHO is: ', num2str(Rabbit_Energy_IHHO)]);

4. 仿真图展示

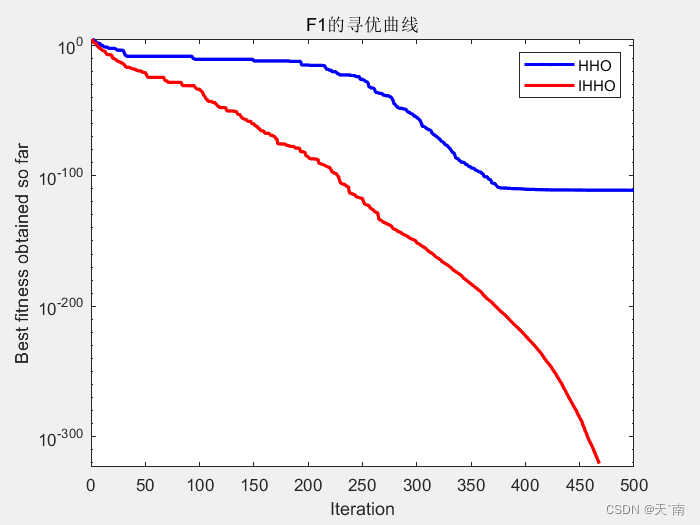
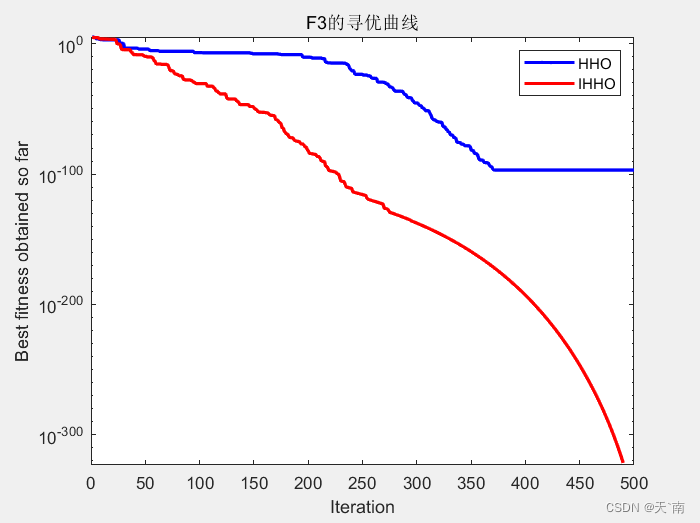
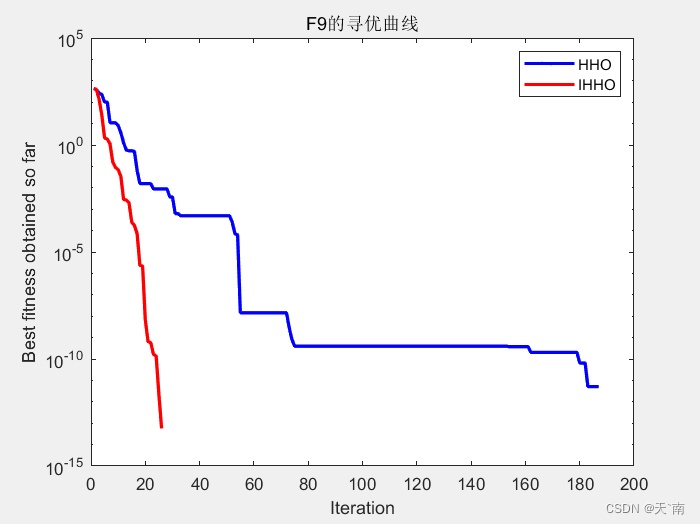
5. 资源获取

A资源获取说明
A资源获取说明