作者：指针不指南吗
专栏：算法篇

🐾人类做题的过程，其实是暴搜的过程🐾

简单介绍一下位运算概念，更多的是写位运算在刷题过程中的应用

1.位运算概述

​ 位运算就是直接对整数在内存中的二进制位进行操作，由于计算机内部就是以二进制来存储数据，位运算是相当快的。

​ 基本的位运算共 6种，分别为按位与、按位或、按位异或、按位取反、左移和右移。

​ 位运算一般有三种作用：

1. 高效地进行某些运算，代替其它低效的方式。
2. 表示集合。（常用于状压DP ）
3. 题目本来就要求进行位运算。

2.位运算符

含义	符号	简述
按位与	a & b	同一得 1
按位或	a | b	有一得 1
按位异或	a ^ b	相同得 0
按位取反	~a	取反
左移	a << b	向左移动，低位补零，高位舍弃
带符号右移	a >> b	向右移动，高位补原有高位，低位舍弃

1. 复合赋值位运算符

   和 += , -= 等运算符类似，位运算也有复合赋值运算符： &= , |= , ^= , <<= , >>= 。（取反是单目运算，所以没有）

2. 数组初始化

   memset(f,0x3f,sizeof(f))

3. 位移运算符

   左移运算符 <<
   二进制 ： 1 -> 10 -> 100 -> 1000
   十进制 ： 1 -> 2  -> 4   -> 8
   综上所述：1 << n  ==  2^n
   右移运算符 >>
   二进制 ： 1000 -> 100 -> 10 -> 1
   十进制 :  8    -> 4   -> 2  -> 1
   综上所述: n >> x  == n / (2^x)
   

4. 运算符优先级

   ~的优先级最高，其次是<<、>>，再次是＆，然后是^，优先级最低的是|。

​ 位运算的优先级 低于 算术运算符（除了取反），而按位与、按位或及异或 低于 比较运算符（详见 运算页面 ），所以使用时需多加注意，在必要时添加括号。

3.位运算应用

3.1整数的奇偶性判断

• 朴素做法

  if(a%2==1)
      //为奇数
  else
      //为偶数
  

• 按位与 -> 二进制的末位为0表示偶数，最末位为1表示奇数

  if(a & 1 != 1)
      //为奇数
  else
      //为偶数
  

3.2有关 2 的幂的应用

将一个数乘（除） 2 的非负整数次幂

// 计算 n*(2^m)
int mulPowerOfTwo(int n, int m)   
{
  return n << m;
}

// 计算 n/(2^m)
int divPowerOfTwo(int n, int m)   
{
  return n >> m;
}

判断一个数是否是2的幂次方，若是，并判断出来是多少次方

题目链接： 力扣 231. 2的幂

​ 将2的幂次方写成二进制形式后，很容易就会发现有一个特点：二进制中只有一个1，并且1后面跟了n个0； 因此问题可以转化为判断1后面是否跟了n个0就可以了

如果将这个数减去1后会发现，仅有的那个1会变为0，而原来的那n个0会变为1；因此将原来的数与去减去1后的数字进行与运算后会发现为零。

   最快速的方法：

  (number & number - 1) == 0

  原因：因为2的N次方换算是二进制为10……0这样的形式(0除外)。按位与上自己-1的位数，这们得到结果为0。例如，8的二进制为1000；8-1=7，7的二进制为111。两者相与的结果为0。计算如下：
     1000
   & 0111
   -------
     0000

代码实现如下：

#include<bits/stdc++.h>
using namespace std;
 
//判断一个数是2的多少次方
int log2(int value)   
{
	int x=0;
	while(value>1)
	{
		value>>=1;
		x++;
	}
	return x;
}
 
int main()
{
	int num;
	scanf("%d",&num);
    
    //使用与运算判断一个数是否是2的幂次方
	if(num&(num-1))     
		printf("%d不是2的幂次方！\n",num);
	else
		printf("%d是2的%d次方！\n",num,log2(num));
    
	return 0;
}

3.3lowbit(x)返回x的最后一位1

​ lowbit(x)：返回x的最后一位1，即一个二进制最低位的1与后边的0组成的数。

​ x = 1010 lowbit(x) = 10

​ x= 101000 lowbit(x) = 1000

​ 实现原理：x & -x = x & (~x + 1)，负数的补码：原码取反加一（利用了负整数的补码特性）

3.4二进制数中1的个数

题目链接：力扣 191.位1的个数

• 朴素做法 -> 使用移位操作，判末位是否为1；移位的次数为32

  int BitCount(unsigned int n)
  {
      unsigned int c =0 ; // 计数器
      while (n >0)
      {
          if((n &1) ==1) // 当前位是1
              ++c ; // 计数器加1
          n >>=1 ; // 移位
      }
      return c ;
  }
  

• 快速做法 -> 迭代n=n&(n-1)，消除最右边的1，计数

  int BitCount2(unsigned int n)
  {
      unsigned int c =0 ;
      for (c =0; n; ++c)
      {
          n &= (n -1) ; // 清除最低位的1
      }
      return c ;
  }
  

3.5求二进制位的某一位是几

n 的二进制中第 k 位数字

• 先把第k为移到最后一位 n>>k

• 看个位是几 x&1

把上面两步综合 即 n>>k&1

应用：输出n=10的二进制

#include<bits/stdc++.h>
using namespace std;

int main()
{
    int n=10;
    
    for(int k=3;k>=0;k--) //从0位开始的（右到左）
        cout<<(n>>k&1);
    
    return 0;
}

3.6交换两个整型变量的值

异或的性质：

1.交换律：可任意交换运算因子的位置，结果不变；

如：a ^ b ^ c = b ^ a ^ c;

2.结合律：即(a ^ b) ^ c == a ^ ( b ^ c) ;

3.对于任何数x, 都有x ^ x = 0, x ^ 0 = x,同自己求异或为0，同0求异或为自己

4.自反性：A ^ B ^ B = A ^ 0 = A, 连续和同一个因子做异或运算，最终结果为自己

例题：int A = 10, int B = 20, 在不引入第3个变量的情况下，交换两个变量的值。

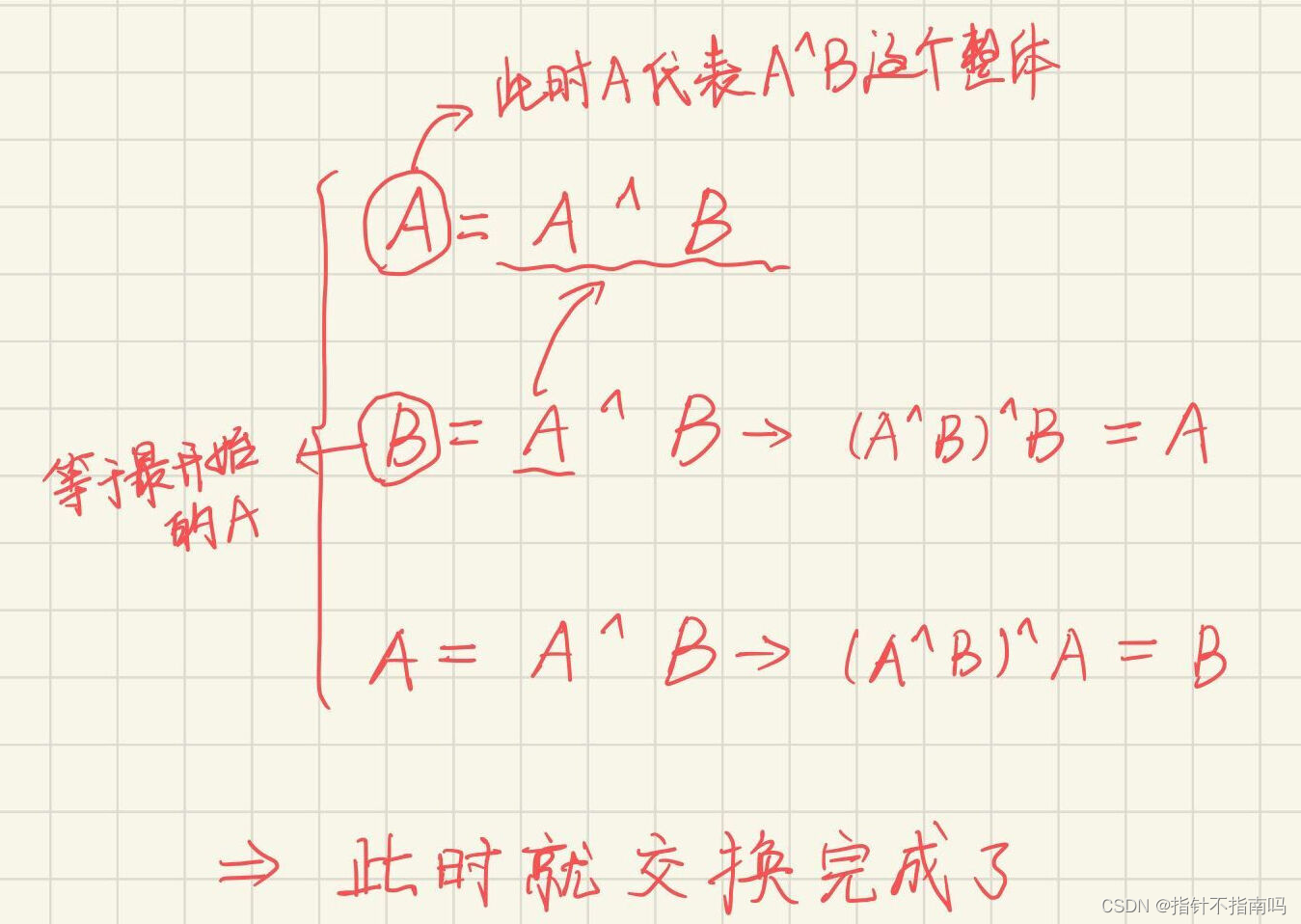
异或法——代码实现

#include<bits/stdc++.h>
using namespace std;

int main()
{
	int A = 10;
    int B = 20;
    printf("交换前A = %d B = %d\n", A, B);
    A = A ^ B;
    B = A ^ B;
    A = A ^ B;
    printf("交换后A = %d B = %d\n", A, B);
    return 0;	
}

3.7数组中x出现的次数

应用一：数组中，只有一个数出现一次，剩下都出现两次，找出出现一次的数
题目链接：力扣 136.只出现一次的数字 |

因为只有一个数恰好出现一个，剩下的都出现过两次，所以只要将所有的数异或起来，就可以得到唯一的那个数，因为相同的数出现的两次，异或两次等价于没有任何操作。

代码实现

int singleNumber(int nums[]) 
{
    int result = 0, n = sizeof(nums)/sizeof(nums[0]);

    for (int i = 0; i < n; i++)
    {
        result ^= nums[i];
    }
    return result;
}

应用二：数组中，只有一个数出现一次，剩下都出现三次，找出出现一次的数

题目链接：力扣 137.只出现一次的数字||

为了方便叙述，我们称「只出现了一次的元素」为「答案」。

由于数组中的元素都在 int（即 32 位整数）范围内，因此我们可以依次计算答案的每一个二进制位是 0还是1。具体地，考虑答案的第 i 个二进制位（i 从0开始编号），他可能为0或者1。对于数组中非答案的元素，每个元素都出现了3次，3次对应第i个二进制位和的3个0或者3个1，无论哪一种情况，他的结果相加（0或者3）都是3的倍数，答案的第 i 个二进制位就是数组中所有元素的第 i 个二进制位之和除以 3 的余数。

这样一来，对于数组中的每一个元素 x，我们使用位运算 （x>>i）&1 得到 x 的第 i 个二进制位，并将它们相加再对 3 取余，得到的结果一定为 0 或 1，即为答案的第 i 个二进制位。

代码实现

int singleNumber(vector<int>& nums) 
{
    int ans = 0;
    for (int i = 0; i < 32; ++i) {
        int total = 0;
        for (int num: nums) {
            total += ((num >> i) & 1);
        }
        if (total % 3) {
            ans |= (1 << i);
        }
    }
    return ans;
}

针对上面进行拓展，如果是数组中，只有一个数出现一次，剩下都出现 k 次 ，找出出现一次的数呢

total % k  //将3改为 k ，对 k 进行取模即可 

---

应用三：如何找数组中唯一成对的那个数

1-10这10个数放在含有11个元素的数组中，只有唯一一个元素重复，其他均只出现一次，要求每个数组元素只能够被访问一次，请设计一个算法，将它找出来 。

位运算中 异或 ^ 的特点，A^A=0 A^0=A ,也就是说，两个相同的数字进行异或结果为0，可以用来消除重复。 可惜，题目要求寻找重复的值，所以，我们对这1001个数字 加上（1 ~ 1000）这1000个数字，这样1~1000所有的数字出现了2次，可以消除，而那个重复的数字由于加了一次，变成了3次，A ^ A ^ A =A。从而得出那个重复的A。

代码实现

int findDouble(int T[])
{
    int res=0; //定义一个返回结果，初始值为0，因为A^0=A
    
    //先对T数组进行异或
    for(int i=0;i<T.length;i++)
    {
        res^=T[i];
    }
    
    //在与1~1000异或
    for(int i=1;i<=1000;i++)
    {
        res^=i;
    }
    return res;
}

3.8快速幂取模

给你三个整数 a,b,p，求 $a^{b}modp$。
题目链接：P1226 【模板】快速幂 | 取余运算

取平方思路

参考文章：https://oi-wiki.org/math/binary-exponentiation/

先看这个式子$a^{2b}=a^2\ast a^b$ ,我们发现取平方可以缩短计算次数，我们可以按照 二进制 来表示幂。那我们来看看幂和二进制之间的关系。

举个例子讲解：例如：$3^{13}=3^{(1101{)}_2}=3^8\ast 3^4\ast 3^1$

是不是发现，这里面只有二进制位是1的才乘到里面，是0的跳过，所以我们只需要用10进制转2进制的方法（不断÷2的余数，直到商为0），即可得到幂数对应的二进制数。**如果某一个二进制位是1，那就将对应的数乘到结果里面，并且底数也翻倍；如果是0，则底数也翻倍。**可看下面的推导过程，这个地方有点绕，跟着过一遍就懂了。

取模定理

(a * b) % p = (a % p * b % p) % p （3） 

乘积的取模等于各个因子取模相乘然后再取模；

取模的运算不会干涉乘法运算，因此我们只需要在计算的过程中取模即可 。

快速幂代码实现

long long binpow(long long a, long long b) 
{
    long long res = 1;
    while (b > 0) 
    {
        if (b & 1) res = res * a;
        a = a * a;
        b >>= 1;
  	}
  	return res;
}

快速幂取模代码实现

long long binpow(long long a, long long b, long long m) 
{
	a %= m;
    long long res = 1;
    while (b > 0) 
    {
        if (b & 1) res = res * a % m;
        a = a * a % m;
        b >>= 1;
  	}
  	return res;
}

4.位运算总结

​ 在刷题中，位运算是一个非常常见的技巧和思路。它能够在一定程度上优化时间和空间复杂度，使得程序更加高效。

​ 在一些需要对二进制进行操作的场景中，位运算能够帮助我们更好地处理问题。比本文介绍的在统计一个数的二进制中有几个1的问题、判断一个数是否是2的幂次方、交换两个整型变量的值等等。