一、快速排序

快速排序的概念相信大家都能理解，下面这个算法是基于同样想法的另一种算法，其中利用到了分区。如果实施正确，这是一种非常有效的算法，在预期的O(n.log n) 时间内运行，乘法常数非常低，大约为2

需要注意的是，该算法的标准版本仅在唯一数据上是线性的。如果元素出现多次，性能会下降。它是一种3向快速排序，它将数据分成三个分区，较低、较高和类似于pivot区。另一个注意的地方就是枢轴的均匀随机化，这是证明算法预期在线性时间运行的重要部分

二、Python算法实现

我们首先来测试在排序时不使用这个排序算法的时间是多少呢？

import numpy as np

def swap(data, i, j):
  data[i], data[j] = data[j], data[i]
def qsort3(data, left, right):
  if left >= right:
    return
  # 选择中心点
  i = np.random.randint(left, right + 1)
  swap(data, left, i)
  pivot = data[left]
  # i表示左分区元素后的序号
  # j表示右分区元素后的序号
  # k表示当前元素的序号
  i, j, k = left, right, left + 1
  # 分割元素[left] + [pivot] + [right]
  while k <= j:
    if data[k] < pivot:
      swap(data, i, k)
      i += 1
    elif data[k] > pivot:
      swap(data, j, k)
      j -= 1
      k -= 1
    k += 1
  # 递归
  qsort3(data, left, i - 1)
  qsort3(data, j + 1, right)
def qsort(data):
  qsort3(data, 0, len(data) - 1)

data = np.random.randint(0, 10, 100)
print(data)

看一下测试结果和运行时间

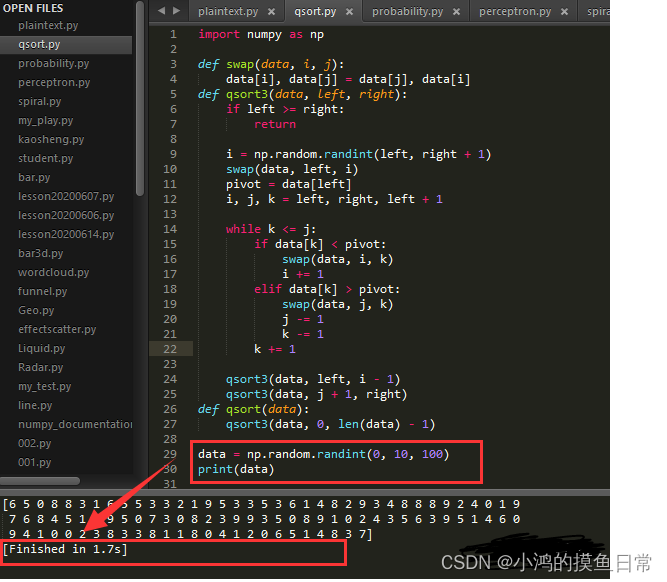
可以看到，此时数据是随机的，完成时间是1.7s

接下来我们把print(data)注释掉，先用算法排序之后再print

import numpy as np

def swap(data, i, j):
  data[i], data[j] = data[j], data[i]
def qsort3(data, left, right):
  if left >= right:
    return

  i = np.random.randint(left, right + 1)
  swap(data, left, i)
  pivot = data[left]
  i, j, k = left, right, left + 1

  while k <= j:
    if data[k] < pivot:
      swap(data, i, k)
      i += 1
    elif data[k] > pivot:
      swap(data, j, k)
      j -= 1
      k -= 1
    k += 1

  qsort3(data, left, i - 1)
  qsort3(data, j + 1, right)
def qsort(data):
  qsort3(data, 0, len(data) - 1)

data = np.random.randint(0, 10, 100)
# print(data)

qsort(data)
print(data)

测试结果

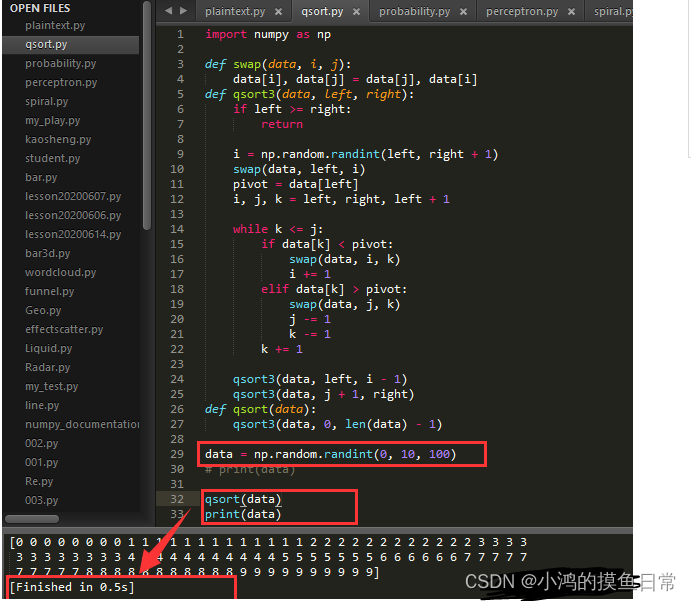
可以看到，在经过算法排序之后，再print(data)，不仅正确排序，时间花费仅为0.5s，运行时间效率提高了