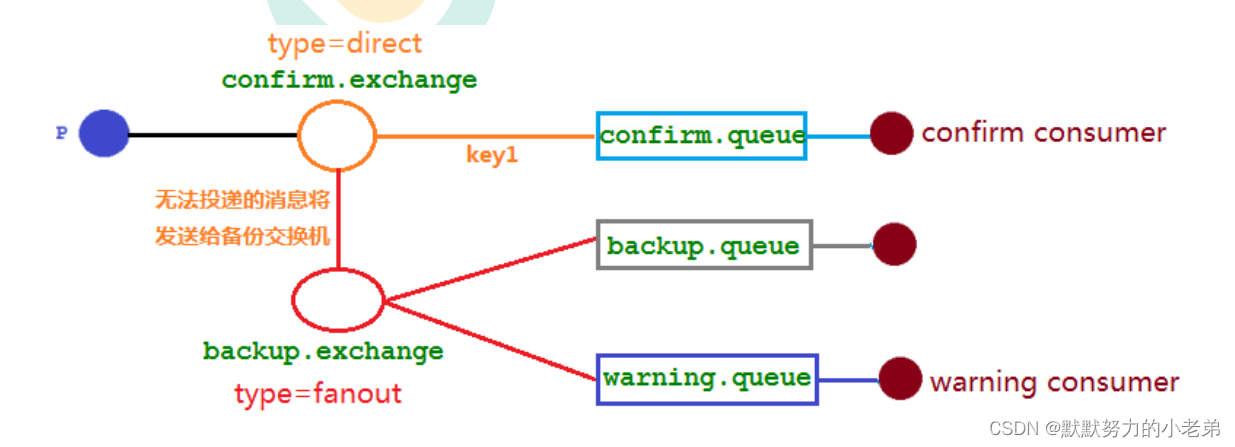
32. 最长有效括号

难度困难2251

给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

示例 1：

输入：s = "(()"
输出：2
解释：最长有效括号子串是 "()"

示例 2：

输入：s = ")()())"
输出：4
解释：最长有效括号子串是 "()()"

示例 3：

输入：s = ""
输出：0

提示：

• 0 <= s.length <= 3 * 104
• s[i] 为 '(' 或 ')'

动态规划

dp定义 : 以s[i]为结尾的字符串,往左最远能推多远 使得是最长的有效括号 该位置的最长有效括号长度就是dp[i]

注意只要是 子串,子序列-->最长.....定义dp数组的定义一般都是以xxx为结尾向左能推多远,并且动态规划的特点要借助前面的答案能推出当前位置的答案,进而从前往后推,推到最后,最终就是答案了....

我们来分析一下题意 :

首先遍历字符串从前往后推导,要么遇到的是左括号,要么遇到的是右括号

• 如果遇到的是左括号,无论怎么往前推都找不到匹配的,左括号无法匹配
• 如果遇到的是右括号,那就要往左推导了
  • 首先我们要找到与当前右括号匹配的左括号的位置
  • 
  • 
  • 
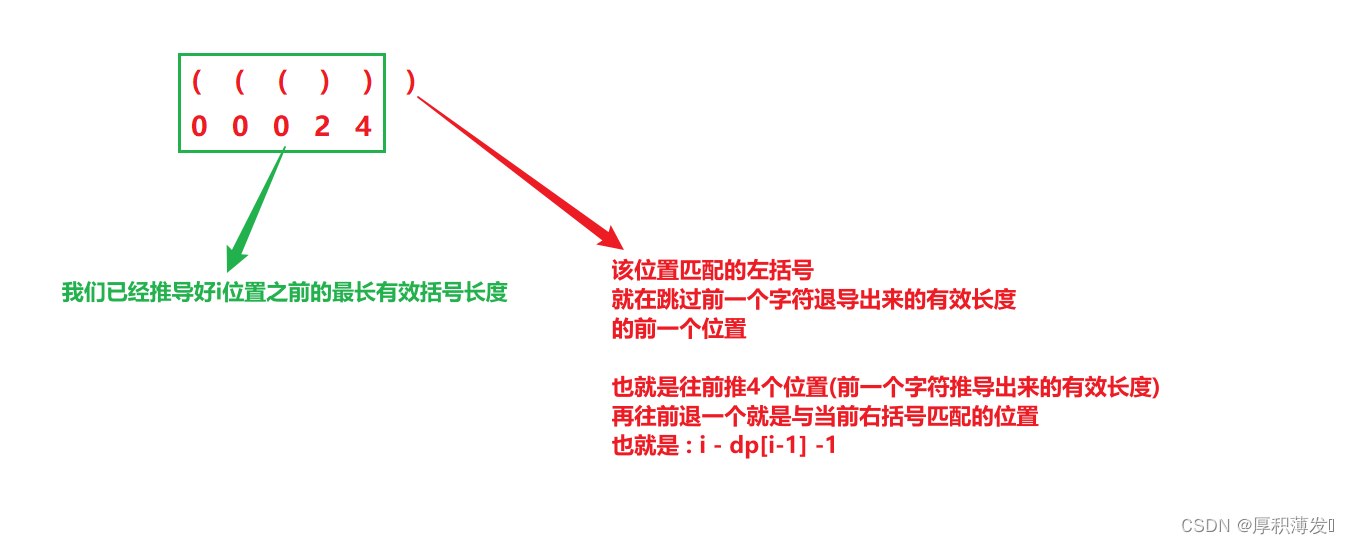
• 当我们找到了与与当前右括号匹配的左括号的位置,答案就是 dp[i-1] + 2,难道这就是答案么 ?
• 

 综上 最长有效括号长度状态转移方程为 :  dp[i] = dp[i-1] + 2 + ((pre-1)>=0 ? dp[pre-1] :0);

dp[i-1] + 2 是指当前右括号找到前面匹配的左括号所以是s[i-1]匹配的有效长度再加上2就是当前最长有效括号长度

dp[pre-1] : 前面可能还有合法的括号,我们也要把它加上 --> dp[pre-1]-->前提是pre合法

class Solution {
    public int longestValidParentheses(String s) {
        if(s==null || s.length() <2) {
            return 0;
        }
        int n = s.length();
        //dp : 以s[i]为结尾的字符串,往左最远能推多远使得是最长的有效括号
        int[] dp = new int[n];
        int res = 0;
        int pre = 0;//记录与当前右括号匹配的左括号的位置
        for(int i =1;i<n;++i) {
            //如果当前是左括号则,往左不可能找到匹配的dp[i]= 0;
            if(s.charAt(i) == ')') {
                //如果当前是右括号
                // (  (  (  )  )  )
                // 0  1  2  3  4  5
                // 0  0  0  2  4  5 - dp[i-1](4) - 1 = 0
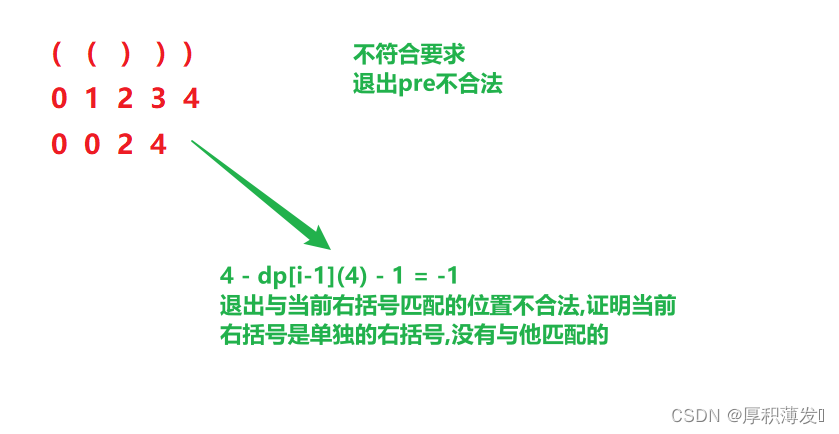
                pre = i - dp[i-1] -1;//记录与当前右括号匹配的左括号的位置
                // 不能匹配 : pre<0
                // (  (  )  )  )
                // 0  1  2  3  4 
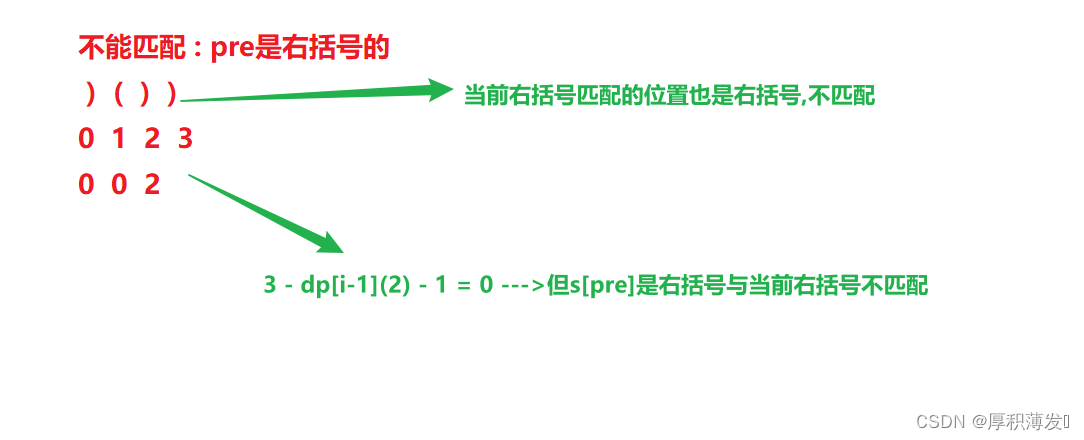
                // 0  0  2  4  4 - dp[i-1](4) - 1 = -1-->当前括号是单独的右括号
                //不能匹配 : pre是右括号的
                // )  (  )  ) 
                // 0  1  2  3
                // 0  0  2  3 - dp[i-1](2) - 1 = 0 --->但s[pre]是右括号与当前右括号不匹配
                if(pre >=0 && s.charAt(pre) == '(') {
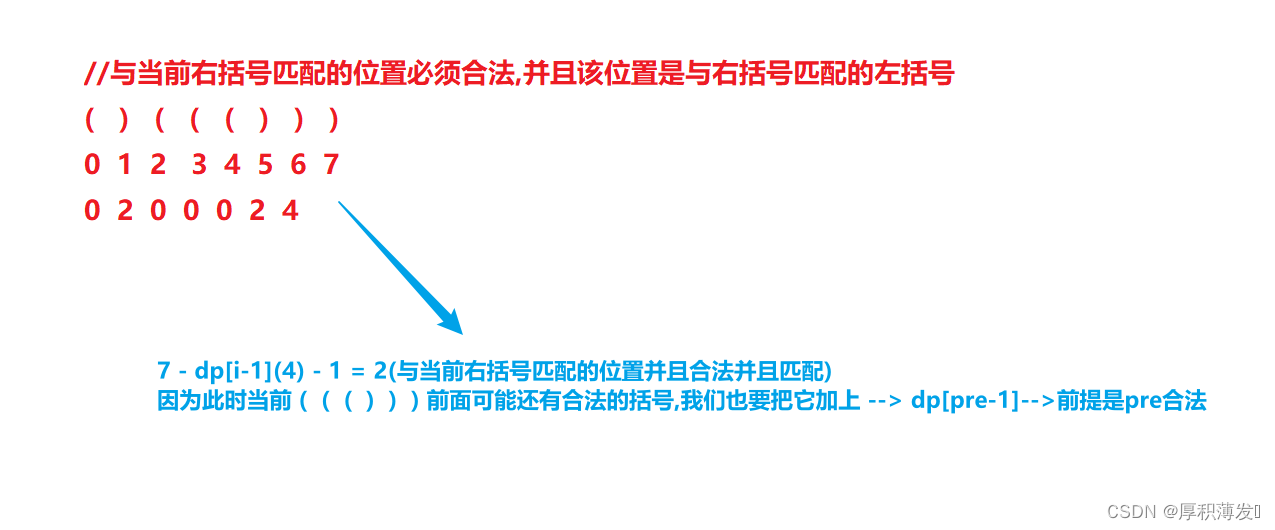
                    //与当前右括号匹配的位置必须合法,并且该位置是与右括号匹配的左括号
                    // (  )  (  (  (  )  )  )
                    // 0  1  2  3  4  5  6  7
                    // 0  2  0  0  0  2  4  7 - dp[i-1](4) - 1 = 2(与当前右括号匹配的位置并且合法并且匹配)
                    // 因为此时当前 (  (  (  )  )  ) 前面可能还有合法的括号,我们也要把它加上 --> dp[pre-1]-->前提是pre合法
                    //dp[i-1] + 2 是指当前右括号找到前面匹配的左括号所以是s[i-1]匹配的有效长度再加上2就是当前最长有效括号长度
                    //dp[pre-1] : 前面可能还有合法的括号,我们也要把它加上 --> dp[pre-1]-->前提是pre合法
                    dp[i] = dp[i-1] + 2 + ((pre-1)>=0 ? dp[pre-1] :0);
                }
            }
            res = Math.max(dp[i],res);
        }
        return res;
    }
}