单调栈的应用

可以用来快速找出左右第一个比$a_i$大或小的数及其下标

830. 单调栈 - AcWing题库

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N =  100010;

int n;
int stk[N],tt;

int main()
{
    
    cin>>n;
    
    for (int i = 0; i < n; i ++ )// 输出左边第一个比他小的数。 
    {
        int x;
        cin >> x;
        while(tt && stk[tt] >= x) tt--;// 栈是非空的，且栈顶元素大于x, 栈顶弹出。
        if(tt) cout << stk[tt] << ' ';
        else
        cout<<-1 <<' ';
        stk[++tt] = x;
    }
   
    return 0;
}

# 读取数组
n = int(input())
nums = list(map(int, input().split()))

# 单调栈
deq = []

# 开始处理数据
for i in range(len(nums)):

    # 从单调栈中弹出不满足升序的数
    while deq and deq[-1] >= nums[i]:
        deq.pop()

    # 此时要么栈空(没有最小),否则栈顶元素就是最近的最小元素
    if len(deq) != 0:
        print(deq[-1], end = " ") 
    else:
        print(-1, end = " ")

    # 将当前数据加入单调栈中(当前数据一定能够保证单调栈升序)
    deq.append(nums[i])

P5788 【模板】单调栈 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
using namespace std;
const int N = 3e6+10;

int f[N],a[N];// f 答案， a是原始数组， 
stack<int> s;//s是单调栈。
int n,tt;

int main()
{
    scanf("%d", &n);
    
    for (int i = 1; i <= n; i ++ )scanf("%d", &a[i]);
    for (int i = n; i >= 1; i -- )// 输出右边第一大于a【i】 的下标
    {
        while(!s.empty() && a[s.top()] <= a[i]) s.pop();// 如果栈不为空， 且栈顶元素小于a[i], 则弹出
        f[i] = s.empty()? 0 : s.top();
        s.push(i);
    }
    for (int i = 1; i <= n; i ++ )printf("%d ",f[i]);
    return 0;
}

84. 柱状图中最大的矩形 - 力扣（LeetCode） (leetcode-cn.com)

思路一

Code

class Solution {
public:
    int largestRectangleArea(vector<int>& h) {
        stack<int> stk;
        int n = h.size();
        if(n == 1) return h[0];
        int ans = 0;
        int left[n], right[n];
        // 左边第一个比h[i]小的下标letf[i]中；右边第一个比h[i]小的下标right[i]中；
        for(int i = 0; i < n; i++)
        {
            while(!stk.empty() && h[stk.top()] >= h[i])stk.pop();
            if(stk.empty())left[i] = -1;
            else left[i] = stk.top();   
            stk.push(i);
        } 
        stk = stack<int>(); // 清空stk；
        for(int i = n-1; i >= 0 ;  i--)
        {
            while(!stk.empty() && h[stk.top()]>=h[i]) stk.pop();
            if(stk.empty()) right[i] = n;
            else right[i] = stk.top();    
            stk.push(i);
        }

        for(int i = 0 ; i<n; i++)
        {
            ans = max(ans, h[i]*(right[i]-left[i]-1));
        }
        return ans;
    }
};

思路二

Code

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        heights.push_back(-1);
        //加入哨兵值，便于原先heights中的最后位置的值弹出
        //因为需要比最后一个值小的值，才能把最后一个值卡在
        //中间计算面积
        stack<int>  stacks;
        stacks.push(-1);
        //栈压入哨兵值，便于heights打头的数组进行操作
        //压入-1为方便计算打头位置的面积
        int   maxs = 0;
        for(int  i=0;i<heights.size();i++)
        {
            while(stacks.top() != -1&&heights[stacks.top()] > heights[i])
            //栈里面后面比前面大的时候才压入，相当于顺序压入，当
            //当前值比栈顶的值小的时候，相当于两个比栈顶小的值把
            //栈顶位置的数卡在中间，比如5，6，2，栈顶数为6
            //此时可以计算栈顶6围成的矩形面积
            {
                int  nums = stacks.top();
                stacks.pop();
                maxs = max(maxs,heights[nums]*(i-stacks.top()-1));
                //面积计算公式为当前下标值*(左右两边的坐标减去1)
            }
            stacks.push(i);
            //栈前面都为比当前值小的时候，无法将栈顶值卡在中间了
            //此时压入当前坐标
        }
        return  maxs;
    }
};

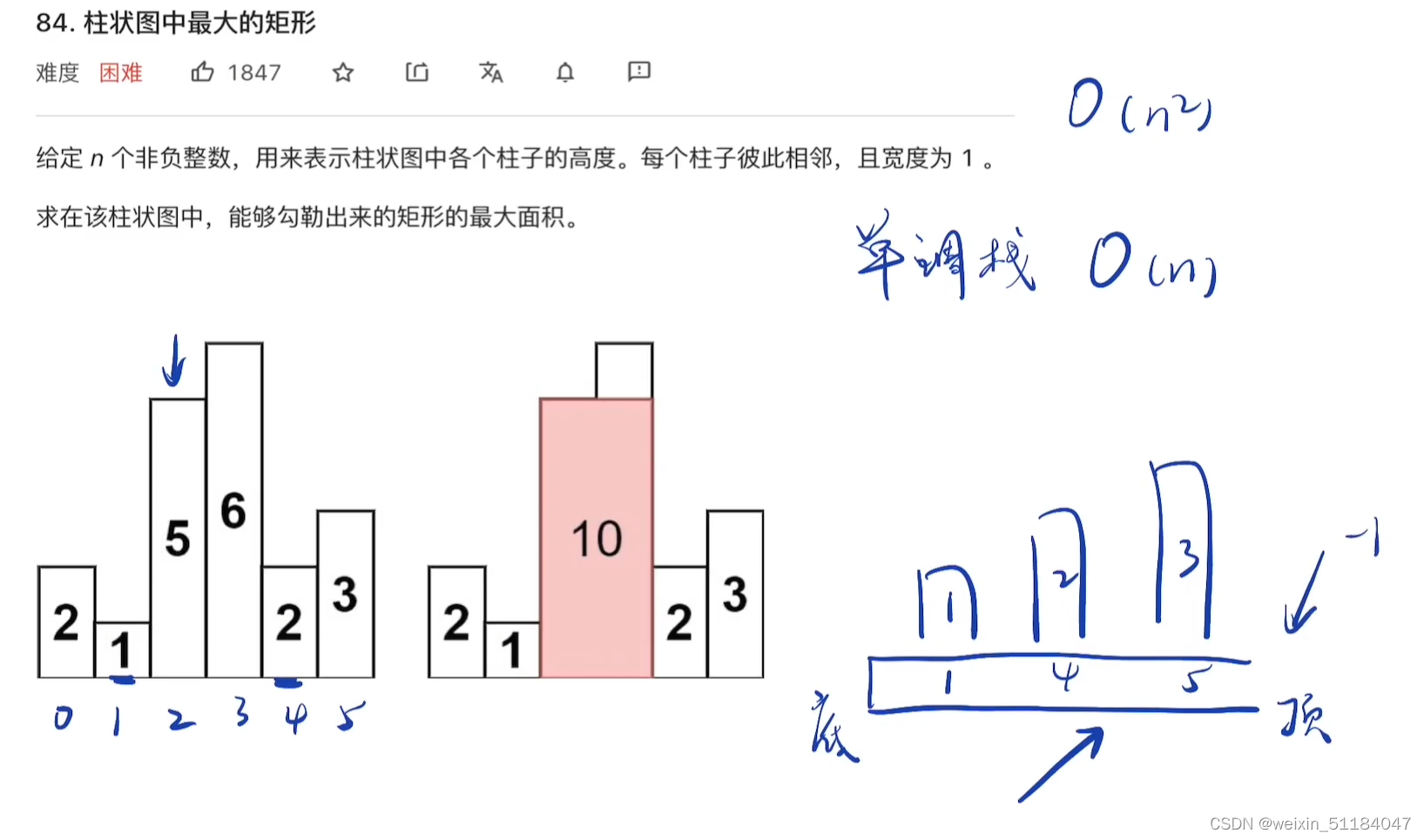
优化思路2

class Solution {
public:
    int largestRectangleArea(vector<int>& h) {
        stack<int> stk;
        h.push_back(-1); // 为了能让栈清空。 在数组后面放一个-1.
        int n = h.size();
        int ans = 0;
        for(int i = 0; i <n; i++)
        {
            while(stk.size() && h[i]<h[stk.top()]) 
            {
                int idx = stk.top();
                stk.pop(); 
                int left = stk.empty()? -1 : stk.top();// 比h[idx]小的左边的第一数的下标。 
                ans = max(ans, (i- left - 1 )* h[idx]);
            }
            stk.push(i);
        }
        return ans;
        
    }
};

1575. 盛水最多的容器 - AcWing题库

双指针算法

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

int a[100100];

int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%d", &a[i]);
    }
    int ans = 0,l = 1,r = n;
   
    while(l<r)
    {
        ans = max(ans,(r-l)*min(a[r],a[l]));
        if(a[l]<a[r]) l++;
        else r--;
    }
    cout << ans;
    return 0;
}

1574. 接雨水 - AcWing题库

双指针算法

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 1e5+10;
int pre_max[N], suf_max[N], h[N],n;

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%d", &h[i]);
        pre_max[i] = max(pre_max[i-1], h[i]);
    }
    
    for (int i = n; i >= 0; i -- )
    {
        suf_max[i]= max(suf_max[i+1],h[i]);
    }
    int ans =0;
    for (int i = 1; i <= n; i ++ )
    {
        ans += min(pre_max[i],suf_max[i]) - h[i];
    }
    cout << ans;
    
    return 0;
}