前言：

1.嵌套调用函数

2.链式访问

3.函数的声明与定义

4.*递归

5.递归与非递归

❤博主CSDN:啊苏要学习

▶专栏分类：C语言◀

C语言的学习，是为我们今后学习其它语言打好基础，C生万物！

开始我们的C语言之旅吧！✈

前言：

在第一篇的基础上，我们接着学习函数相关的知识。虽然都是基础知识，但干货满满，读来没有新的知识收获，也有复习的奇效。

1.嵌套调用函数

在C语言中，调用函数是非常常见的。我们需要使用函数来解决问题，自然就需要把函数给调出来使用。那么什么是嵌套调用呢？我们看下面的代码：

#include <stdio.h>


void put_word(int n)
{
    if (11 == n)
        printf("I miss you!\n");
    if (13 == n)
        printf("I want to say\n");
}
void put_line()
{
    int a = 0;
    int i = 0;
    printf("Hello long time no see!\n");
    for (i = 0; i < 2; i++)
    {
        if (i != 1)
        {
            printf("你可以输入两次\n");
        }
        printf("请输入你要听的字符数(13，11)>:");
        scanf("%d", &a);
        put_word(a);
    }

}
int main()
{
    put_line();
    return 0;
}

这段代码的逻辑是：先在main函数里调用put_line函数；进入到put_line函数里面再调用了put_word函数；这里是多层调用，A调用B，B调用C来完成"我想你"这段有趣的输出。这种就是函数的嵌套调用。

函数的嵌套调用是必要的，比如在生成汽车的时候，原材料从哪里来，各种原材料加工厂是原材料变成相应的部件，最后组装在一起变成汽车。在计算机中，每个函数就是一个部件，最后有机组合(嵌套调用)在一起，完成程序任务。

补充:

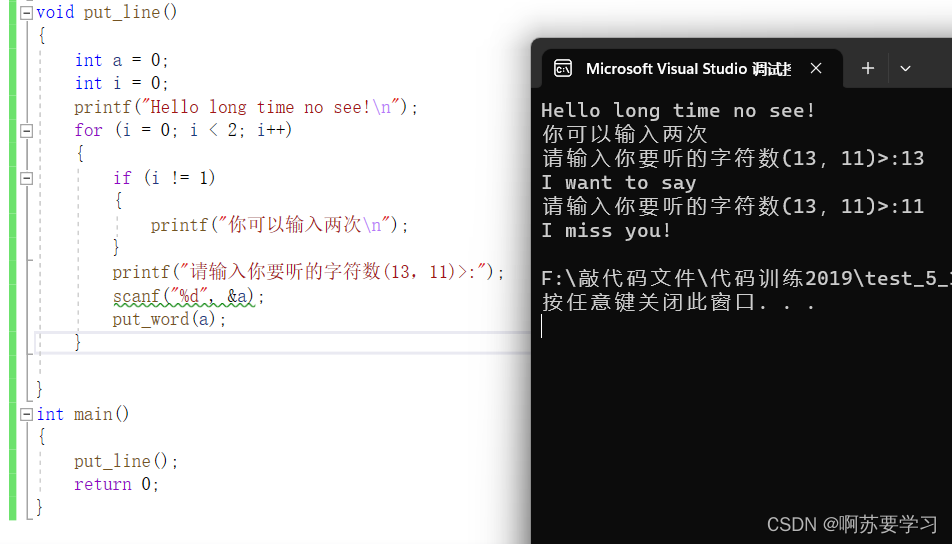
相信大家看完这段代码后，印象会更深刻一点~

2.链式访问

链式访问是将函数的返回值作为一个函数的参数使用。

#include <stdio.h>
#include <string.h>

int main()
{
    int len = strlen("abcdef");
    printf("%d\n", len);
    printf("%d\n", strlen("abcdef"));
    return 0;
}

printf函数参数为strlen("abcdef")利用的就是函数的链式访问，strlen返回字符串的长度，这个长度作为printf函数的参数被打印出来。

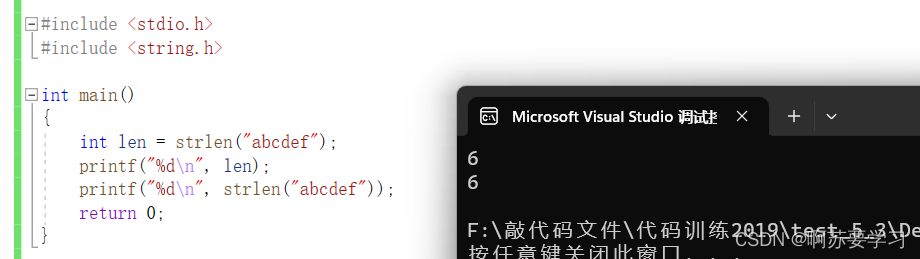
它的效果和使用整型len接收strlen返回的长度，并打印len是一样的。

我们接下来看这样一段代码，感受函数的链式调用：

#include <stdio.h>

int main()
{
    printf("%d", printf("%d", printf("%d", 43)));
    return 0;
}

这段代码将打印什么呢？首先最外层的printf要打印一个整型值，它要看里层printf函数的返回值是多少；里层函数要打印一个整型值，它要看最里层printf函数的返回值是多少；这个时候，从最外层的printf函数打印，层层往里像一条链一样串起来。

现在已经分析到最里层的printf函数了，它打印了43这个整型，但我们不知道printf函数打印完后，返回什么东西，这时候我们得上网站查一查：cplusplus.com

具体的使用方法可以快速阅读一下上一篇函数知识讲解如何学习库函数：链接

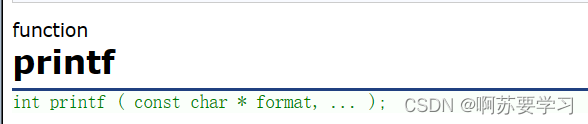
得知printf函数的返回值是成功读取到字符的个数；那么最里层printf函数成功读取到43这两个字符，返回值是2；上面的代码就变成了printf("%d", printf("%d", 2));这样子了。接着就是里层打印2，成功读取的字符个数是1，返回值为1，变成printf("%d", 1);。

最终在屏幕上显示的就是：

3.函数的声明与定义

函数的使用必须遵循先声明后使用的原则。

#include <stdio.h>

int Add(int, int);//声明Add函数
int main()
{
    int a = 10;
    int b = 20;
    printf("%d\n", Add(a, b));
    return 0;
}

int Add(int x, int y)//定义函数
{
    return x + y;
}

声明函数的时候，需要指出它的返回类型、函数名、函数的参数类型，由于声明是一条语句，不要漏了最后的分号。

补充：函数声明参数的时候，可以只写类型，而不用写名字。我们不必写int Add(int x, int y);。

由于程序的执行流程是从上往下执行的，程序入口是main函数，所以将定义放在函数使用之前，就可以不用声明。

#include <stdio.h>

int Add(int x, int y)//定义函数
{
    return x + y;
}

int main()
{
    int a = 10;
    int b = 20;
    printf("%d\n", Add(a, b));//已经知道Add是什么样的函数了
    return 0;
}

这是一种特殊的声明，定义声明。主旨思想就是：编译器需要知道你使用的函数是什么，要么定义在我使用之前，要么你告诉我这个函数是什么。

4.*递归

函数自己调用自己叫做递归；递归往往能将一个大量重复的计算用简洁少量的代码写出来，递归的本质是大事化小。我们先来看一个代码：

#include <stdio.h>

//打印12345的每一位数
void print(int n)
{
    if(n > 9)
    {
        print(n/10);//打印1234的每一位数
    }
    printf("%d ", n%10);//打印5
    
}

//打印1234的每一位数
//void printf(int n)
//{
//   if(n > 9)
//    {
//        print(n/10);//打印123的每一位数
//    }
//    printf("%d ", n%10);//打印4
//}
//...
//...
//打印1的每一位数
//void printf(int n)
//{
//      if(n > 9)
//      {
//          print(n/10);
//      }
//      printf("%d ", n%10);//1
//}

int main()
{
    int n = 0;
    scanf("%d", &n);//12345
    //将n的每一位打印出来
    print(n);
    return 0;
}

想求数字12345的每一位，可以使用取模取商交替使用的方法求。12345%10 = 5；得到数字5。12345/10得到数字1234；再将1234%10 = 4；得到数字4。1234/10得到数字123........。

打印12345的每一位数，我们定义一个print函数用来求之。利用大事化小的本质，可以这样思考：使用print函数打印1234的每一位+打印数字5，再将（打印数字1234的每一位）分解成，打印123每一位+打印数字4.......。

这个比较难理解，再过一会下面有图解，保证清晰易懂~。

从这个思考里面我们可以得出：每次打印最后一位是需要打印数字每一位的最后一位，也就是说当我需要打印数字12345的每一位的时候，我需要打印5，然后在打印数字1234的每一位的时候，我需要打印4。以此类推，直到当我在打印数字1的时候，我把最后一位1打印出来，已经没有数字了，程序停止。

注意的要点是：递归需要有限制，没有限制条件或限制条件不恰当都会导致栈溢出。

在调用函数的时候，函数需要在栈上开辟空间，这个过程叫做压栈，如果递归一直持续下去没有完结，栈上的空间都被占满了，没有栈空间程序就自动挂掉，并给警告说栈溢出。

所以使用递归的时候，有两个注意点：

进行递归是有限制条件的，不是可以任何情况都可以递归下去。
每进行一次递归调用，都会使递归条件越来越接近结束条件。

在求数字的每一位的时候，进行递归的条件是大于9，也就是要有两位数才进行递归，如果只有一位数，那直接取余打印出来就OK了。每次递归n的值都会少一位，所以这个递归不会出现很大的问题。最重要的一点来了：用画图法来解释刚刚这道代码题，保证能理解透彻。

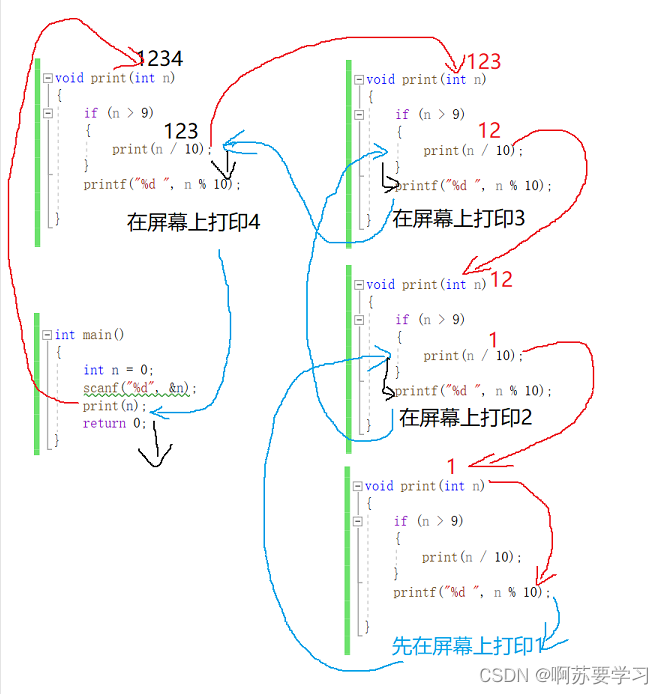
一层一层往下递推下去，限制条件限制继续往下递归的时候，开始往回退，一层一层处理，结束。

5.递归与非递归

一般能用递归解决的问题，都可以使用循环解决，因为递归实际上也相当于是在重复做一件事，只不过递归不像循环一样一点都不变，但仍可以使用循环代替。是使用循环还是递归呢？我们需要结合具体情况。

求斐波那契数列的第n的数：

#include <stdio.h>

//递归实现
int Fib(int n)
{
    if(n <= 2)
        return 1;
    else
        return Fib(n-2)+Fib(n-1)；
}
int main()
{
    int n = 0;
    scanf("%d", &n);
    int ret = Fib(n);
    printf("%d\n", ret);
}

斐波那契数列的规律是：1 1 2 3 5 8 13 21 34 55.......、从第三各个数开始，每个数都是前两个数的和。递归的实现思路是：如果求的是第一，第二个斐波那契数列，就返回1；如果不是就返回求n-1和n-2的斐波那契数列值。这样一直递归求下去直到n<=2时到达限制条件，不再递归下去了，开始回溯。

假如我们求的是第五十个斐波那契数列，那么由代码可知，我们会求第48斐波那契数列值和第49斐波那契数列值；48再求46和47的，49在求47和48的；这样每次递归下去，求的数值都翻一倍，重复计算很多，效率非常低下。我们可以用一个计数器，看看求40的斐波那契额数列值时，Fib（3）被重复计算了多少次！

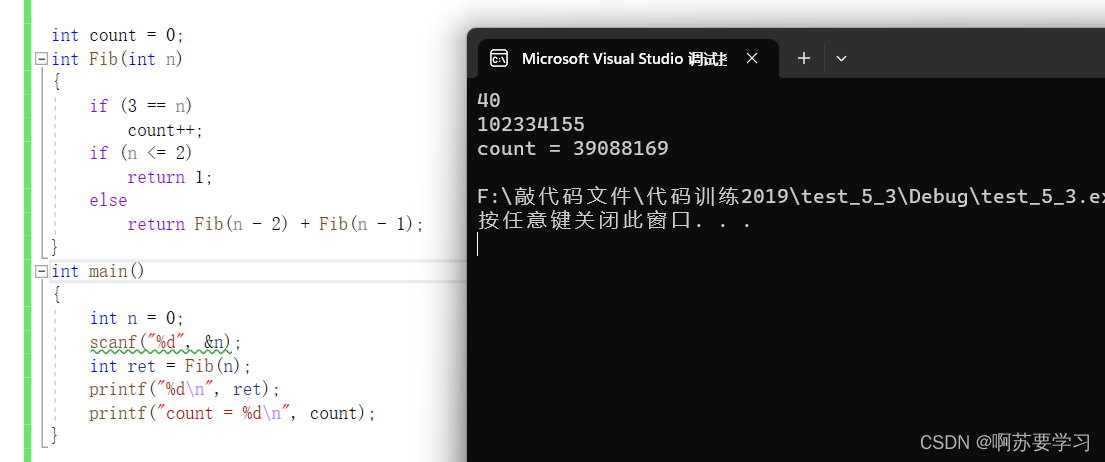
被重复计算了3千9百多万次！！！这时候用递归来求是不可以取的。我们看循环求解斐波那契额数列。

#include <stdio.h>


int Fib(int n)
{
    int a = 1;
    int b = 1;
    int c = 1;
    while (n >= 3)
    {
        c = a + b;
        a = b;
        b = c;
        n--;
    }
    return c;
}

int main()
{
    int n = 0;
    scanf("%d", &n);
    int ret = Fib(n);
    printf("%d\n", ret);
    return 0;
}

循环求解斐波那契数列就是，1 1 2 3 5 8.....、a代表Fib(n-2)、b代表Fib(n-1)，每次循环都把Fib(n-2)和Fib(n-1)的和赋给cFib(n)，然后整体将a、b整体向右移。当n=3时，这个循环操作一次，n=4时，循环操作两次，也就是两次将a、b的和赋值给c，符合要求斐波那契额数列的求法。

这个算法可以很快的算出n = 50时的斐波那契数列值。这时我们会选择用循环解决这个问题。

总结：什么时候使用递归呢？如果递归的实现比较简单，而且不需要耗费太多时间，我们就可以选择递归。即使递归写起来比较方便，但耗时太久了，我们反而会选择，代码篇幅较长的循环来解决。

文已至此，函数的内容就讲完啦~，感谢观看，咱们下篇见。