人工智能 回归问题

1943 年，心理学家沃伦·麦卡洛克
(Warren McCulloch)和数理逻辑学家沃尔特·皮茨(Walter Pitts)通过对生物神经元的研究，
提出了模拟生物神经元机制的人工神经网络的数学模型 ，这一成果被美国神经学家弗
兰克·罗森布拉特(Frank Rosenblatt)进一步发展成感知机(Perceptron)模型 ，这也是现代
深度学习的基石。

典型生物神经元结构：

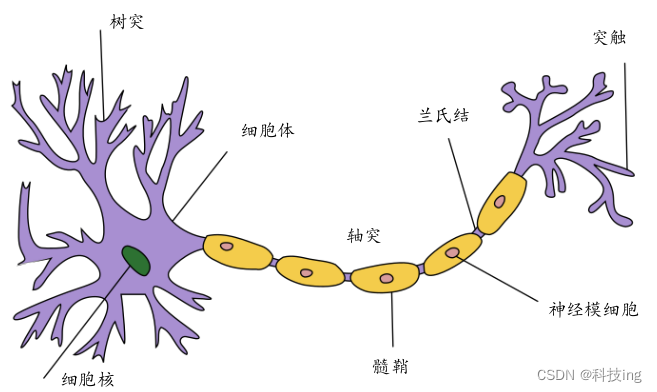
我们把生物神经元(Neuron)的模型抽象为数学结构：

神经元输
入向量𝒙 = [𝑥 1 , 𝑥 2 , 𝑥 3 , … , 𝑥 𝑛 ] T ，经过函数映射：𝑓 𝜃 : 𝒙 → 𝑦后得到输出𝑦，其中𝜃为函数𝑓自
身的参数。考虑一种简化的情况，即线性变换：𝑓(𝒙) = 𝒘 T 𝒙 + 𝑏，展开为标量形式：
𝑓(𝒙) = 𝑤 1 𝑥 1 + 𝑤 2 𝑥 2 + 𝑤 3 𝑥 3 + ⋯ + 𝑤 𝑛 𝑥 𝑛 + 𝑏

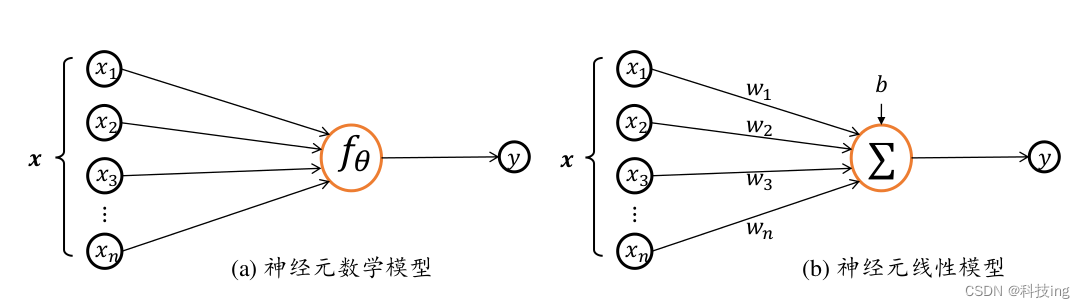
神经元数学模型可进一步简化为：
𝑦 = 𝑤𝑥 + 𝑏 公式(1)

训练目的就是给定训练数据 (x,y) 的集合，推导合适的 w b 的过程，使得 误差最小
假设误差为 e

神经元模型数学表达式：

𝑦 = 𝑤𝑥 + 𝑏 + e 公式(2)

误差函数

均方误差(Mean Squared Error，简称MSE）公式(3):

$$MSE=\frac{1}{n}\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$

其中 $${\hat{y}}_i$$ 是真实值
其中$$y_i$$ 是模型输出

优化方法

梯度下降算法(Gradient Descent)

是神经网络训练中最常用的优化算法，配合强大的图形处理芯片 GPU(Graphics Processing Unit)的并行加速能力，非常适合优化海量数
据的神经网络模型

• 我们为了求最小误差 MSE 关于 模型参数 w b 的梯度(偏导数)

改下公式(3)如下：

$$L=\frac{1}{n}\sum _{i=0}^n\left(w\ast x^i+b-y^i\right)$$

需要优化的模型参数是𝑤和𝑏，因此我们按照

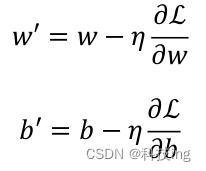
方式循环更新参数，

下面Epoch 是循环迭代计算的次数，MSE 已经越来越小，对于给定的条件 MSE<阈值，可以认为误差MSE符合要求，模型训练达到要求

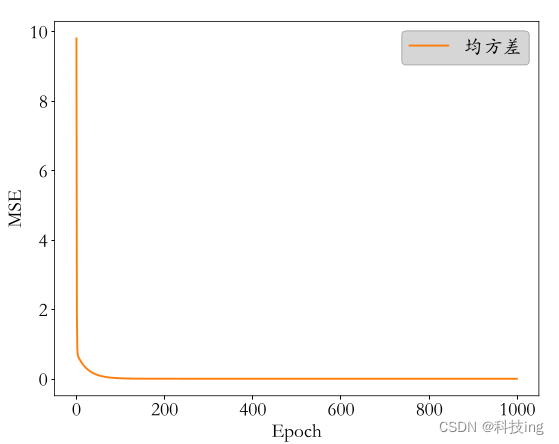
回归(Regression)

首先假设𝑛个输入的生物神经元的数学模型为线性模型之后，只采样𝑛 + 1个数据点就可以估计线性模型的参数𝒘和𝑏。引入观测误差后，通过
梯度下降算法，我们可以采样多组数据点循环优化得到𝒘和𝑏的数值解。

给定数据集𝔻，我们需要从𝔻中学习到数据的真实模型，从而预测未见过的样本的输出值。在假定模型的类型后，学习过程就变成了搜索模型参数的问题，比如我们假设神经元为线性模型，那么训练过程即为搜索线性模型的𝒘和𝑏参数的过程。训练完成后，利用学到的模型，对于任意的新输入𝒙，我们就可以使用学习模型输出值作为真实值的近似。从这个角度来看，它就是一个连续值的预测问题。

在现实生活中，比如股价的走势预测、天气温度湿度预测、年龄预测、交通流量预测。对于预测值是连续的实数范围，或者属于某一段连续的实数区间，我们把这种问题称为回归(Regression)问题。
如果使用线性模型去逼近真实模型，那么我们把这一类方法叫做线性回归(Linear Regression，简称 LR)