70. 爬楼梯
和377. 组合总和 Ⅳ (opens new window)基本就是一道题了。本题代码不长，题目也很普通，但稍稍一进阶就可以考察完全背包
class Solution {
public:
int climbStairs(int n) {
vector<int> nums = {1,2};
vector<int> dp(n+1,0);
dp[0] = 1;
for(int j = 0; j <=n; j++){
for(int i = 0; i < nums.size(); i++){
if(j >= nums[i]) dp[j] += dp[j - nums[i]];
}
}
return dp[n];
}
};
322. 零钱兑换
动态规划五部曲
1、确定dp[j]的含义
dp[j] 凑成 j 的最少硬币的个数
2、确定递推公式
比如想凑成3，
如果手里有1，那么最小个数就是dp[2]+1
如果手里有2，那么最小个数就是dp[1]+1
如果手里有3，那么最小个数就是dp[0]+1
dp[j] = min（dp[j] , dp[j-nums[i]] + 1）
3、确定初始值
dp[0] = 0
其余值应给 INT_MAX。
最终dp[j] == INT_MAX 就返回-1
4、确定遍历顺序
首先这是个完全背包，背包容量从小到大遍历。其次，{5，5，1} 和{1，5，1}的组合大小都是3，所以两层for循环无所谓遍历顺序。
5、验证
coins = [1, 2, 5], amount = 11
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount+1,INT_MAX);
dp[0] = 0;
for(int j = 1; j <= amount; ++j){
for(int i = 0; i < coins.size(); ++i){
if(j >= coins[i] && dp[j - coins[i]] != INT_MAX) dp[j] = min(dp[j],dp[j - coins[i]] + 1);
}
}
return dp[amount] == INT_MAX ? -1 : dp[amount];
}
};
279. 完全平方数
1、dp[j] : 构成 j 的完全平方数的最小数量
2、dp[j] = min( dp[j] , dp[j - i * i ] + 1)
3、初始化
1 <= n <= 104，所以dp[0]无意义
dp[1] = 1, 其余值给INT_MAX
4、完全背包，求个数所以不用管两个for的内外
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n+1,INT_MAX);
dp[0] = 0;
dp[1] = 1;
for(int i = 1; i <= n ; ++i){
for(int j = i*i; j <= n; ++j){
if(dp[j-i*i] != INT_MAX) dp[j] = min(dp[j], dp[j - i*i] + 1);
}
}
return dp[n] ;
}
};
139. 单词拆分
本题与回溯中：分割回文子串的思路是一样的，通过分割字符串，得到单词，再去单词列表中寻找该单词是否存在。
回溯写法：
其中的memory数组，与之前组合问题中的去重数组作用一致。本题中通过在对应的位置设置false，来标记该字母后的字符串没有可分割的方法。例如：
cat sand og，在index = 7的地方设置false（og），
cats and og，当再一次分割到index = 7的时候，就不再进入for循环判断og有无合适的分割方法，而是直接通过memory[7] = false 返回false。
时间复杂度还是O(2n)，但是比没有memory数组的情况好很多。
namespace jj22 {
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
vector<bool> memory(s.size(), 1); // -1 表示初始化状态
return backtracking(s, wordSet, 0,memory);
}
bool backtracking(string s,unordered_set<string>& wordSet,int startIndex, vector<bool>& memory) {
if (startIndex >= s.size())return true;
if (!memory[startIndex]) return memory[startIndex];
for (int i = startIndex; i < s.size(); ++i) {
string word = s.substr(startIndex, i - startIndex + 1);
if (wordSet.find(word) != wordSet.end() && backtracking(s, wordSet, i + 1,memory)) {
return true;
}
}
memory[startIndex] = false; // 记录以startIndex开始的子串是不可以被拆分的
return false;
}
};
void test() {
string s = "catsandog";
vector<string> wordDict = { "cats", "dog", "sand", "and", "cat" };
Solution ss;
bool temp = ss.wordBreak(s, wordDict);
int a = 10;
}
}
背包解法：
首先，本题的物品就是各个单词，背包容量是字符串长度。由于物品可以重复拿取，所以是完全背包问题。
五部曲：
1、dp数组的含义
dp[j] : 长度为j 的字符串能否被单词列表里的单词组成
2、递推公式
当 i < j 时，如果dp[i] = true(即 dp[i] 长度为 i 的字符串能否被单词列表里的单词组成)，
并且 i+1 到 j 组成的单词在列表中能找到，则dp[j] = true
3、初始化
dp[0] = true
其余为false
例如：
string s = "catsandog";
vector<string> wordDict = { "cats", "dog", "sand", "and", "cat" };
dp[2] , j = 2, i = 0时，0-2的cat可以被找到，并且依赖于dp[0]，所以dp[0] 必须为true
4、遍历顺序
构成字符串的单词顺序是唯一的，所以是求排列问题，{1，5}和{5，1}是两种不同的答案。
所以外层遍历背包，内层遍历物品。
5、举例推导dp[i]
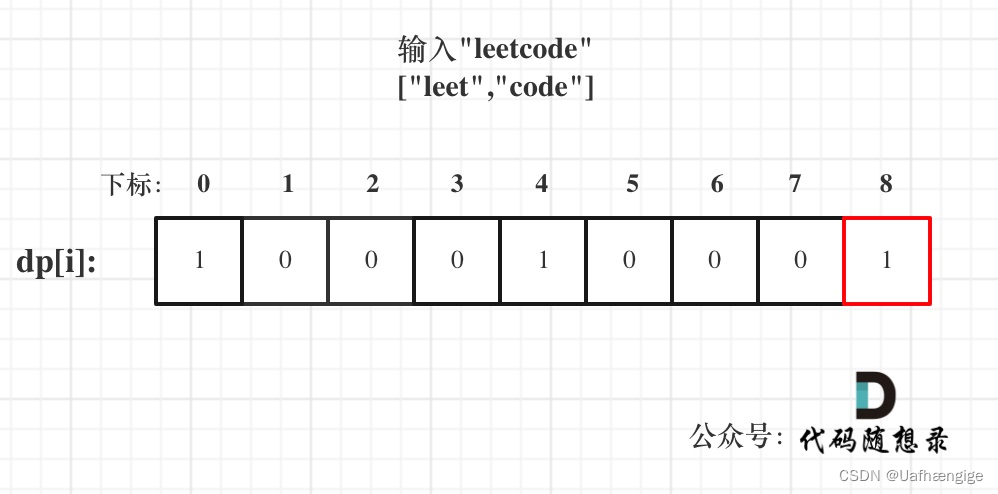自己写的：内层遍历直接就是单词列表
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
vector<bool> dp(s.size() + 1, 0);
dp[0] = true;
for (int j = 0; j <= s.size(); ++j) {
for (int i = 0; i < wordDict.size(); ++i) {
string temp = wordDict[i];
if (j >= temp.size() && dp[j - temp.size()] == true && s.substr(j - temp.size(), temp.size()) == temp) dp[j] = true;
}
}
return dp[s.size()];
}
};
卡哥写的：内层是在从0开始遍历字符串，到 j 。看i-j组成的单词能否被找到
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
vector<bool> dp(s.size() + 1, false);
dp[0] = true;
for (int i = 1; i <= s.size(); i++) { // 遍历背包
for (int j = 0; j < i; j++) { // 遍历物品
string word = s.substr(j, i - j); //substr(起始位置，截取的个数)
if (wordSet.find(word) != wordSet.end() && dp[j]) {
dp[i] = true;
}
}
}
return dp[s.size()];
}
};
多重背包理论基础
每件物品最多有Mi件可用，把Mi件摊开，其实就是一个01背包问题了。
例如：
背包最大重量为10。
物品为：
重量 价值 数量
物品0 1 15 2
物品1 3 20 3
物品2 4 30 2
问背包能背的物品最大价值是多少？
和如下情况有区别么？
重量 价值 数量
物品0 1 15 1
物品0 1 15 1
物品1 3 20 1
物品1 3 20 1
物品1 3 20 1
物品2 4 30 1
物品2 4 30 1
毫无区别，这就转成了一个01背包问题了，且每个物品只用一次。
void test_multi_pack() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
vector<int> nums = {2, 3, 2};
int bagWeight = 10;
for (int i = 0; i < nums.size(); i++) {
while (nums[i] > 1) { // nums[i]保留到1，把其他物品都展开
weight.push_back(weight[i]);
value.push_back(value[i]);
nums[i]--;
}
}
vector<int> dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
for (int j = 0; j <= bagWeight; j++) {
cout << dp[j] << " ";
}
cout << endl;
}
cout << dp[bagWeight] << endl;
}
![[stable-diffusion-art] 指北-3 inpainting](https://img-blog.csdnimg.cn/img_convert/f34c6429f8c09adae90e1bdfb4cd75cf.png)
