大家好,我是带我去滑雪!
本期为大家介绍决策树算法,它一种基学习器,广泛应用于集成学习,用于大幅度提高模型的预测准确率。决策树在分区域时,会考虑特征向量对响应变量的影响,且每次仅使用一个分裂变量,这使得决策树很容易应用于高维空间,且不受噪声变量的影响。这是因为如果特征向量包含噪声变量(对响应变量无作用的变量),那么该特征向量将不会被选为分裂变量,故不影响决策树的建模。在某种意义上,决策树的分区预测更具智慧,可视为自适应邻近法。如果将决策树用于分类问题,则称为分类决策树,如果将决策树用于回归问题,则称为回归决策树。下面介绍两个python案例,练习实操。
目录
1、分类决策树案例
(1)导入相关模块与数据
(2)数据清洗与划分训练集、测试集
(3)构建决策树
(4)考察成本复杂性参数与叶节点总不纯度的关系
(5)通过10折交叉验证选择最优的超参数ccp_alpha值,并拟合模型
(6)计算每个变量重要性并进行可视化
(7)使用测试集进行预测,并计算混淆矩阵
(8)计算预测准确率与灵敏度、kappa指标
(9)以0.1作为临界值重新进行预测,计算混淆矩阵与预测准确率、灵敏度
2、回归决策树案例
(1)导入数据与相应模块
(2)划分训练集和测试集,构建决策树模型,并绘制决策树
(3)考察成本复杂性超参数与叶节点总均方误差的关系
(4)通过10折交叉验证选择最优超参数alpha值,并以此构建决策树模型,绘制决策树
(5)计算各变量的重要性值,并进行可视化
(6)使用测试集进行预测,画出预测值与实际值的散点图
1、分类决策树案例
使用葡萄牙银行市场营销的数据集bank-additional.csv来进行分类决策树操作,该数据集的特征变量包括客户的年龄(age)、职业类型(job)、婚姻状况(marital)、受教育程度(education)、是否信用违约(default)、是否有房贷(housing)、是否有个人贷款(loan)、工作单位人数(nr.employed)、消费者信心指数(cons.conf.indx)等共计20个,响应变量y为二分类变量,表示在接到银行的直销电话后,客户是否会购买银行定期存款产品。
(1)导入相关模块与数据
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold, StratifiedKFold
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeRegressor,export_text
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.metrics import cohen_kappa_score
bank = pd.read_csv(r"E:\工作\硕士\博客\博客28-分类决策树与回归决策树\bank-additional.csv", sep=';')
bank.shape#考察数据框维度
pd.options.display.max_columns = 30 #增大pandas数据框的最大显示列数
bank输出结果:
age job marital education default housing loan contact month day_of_week duration campaign pdays previous poutcome emp.var.rate cons.price.idx cons.conf.idx euribor3m nr.employed y 0 30 blue-collar married basic.9y no yes no cellular may fri 487 2 999 0 nonexistent -1.8 92.893 -46.2 1.313 5099.1 no 1 39 services single high.school no no no telephone may fri 346 4 999 0 nonexistent 1.1 93.994 -36.4 4.855 5191.0 no 2 25 services married high.school no yes no telephone jun wed 227 1 999 0 nonexistent 1.4 94.465 -41.8 4.962 5228.1 no 3 38 services married basic.9y no unknown unknown telephone jun fri 17 3 999 0 nonexistent 1.4 94.465 -41.8 4.959 5228.1 no 4 47 admin. married university.degree no yes no cellular nov mon 58 1 999 0 nonexistent -0.1 93.200 -42.0 4.191 5195.8 no ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 4114 30 admin. married basic.6y no yes yes cellular jul thu 53 1 999 0 nonexistent 1.4 93.918 -42.7 4.958 5228.1 no 4115 39 admin. married high.school no yes no telephone jul fri 219 1 999 0 nonexistent 1.4 93.918 -42.7 4.959 5228.1 no 4116 27 student single high.school no no no cellular may mon 64 2 999 1 failure -1.8 92.893 -46.2 1.354 5099.1 no 4117 58 admin. married high.school no no no cellular aug fri 528 1 999 0 nonexistent 1.4 93.444 -36.1 4.966 5228.1 no 4118 34 management single high.school no yes no cellular nov wed 175 1 999 0 nonexistent -0.1 93.200 -42.0 4.120 5195.8 no 4119 rows × 21 columns
(2)数据清洗与划分训练集、测试集
bank = bank.drop('duration', axis=1)#使用drop()方法去除无效变量duration
X_raw = bank.iloc[:, :-1]#取出所有的特征变量,不含最后一列的响应变量
X = pd.get_dummies(X_raw)#对所有的特征变量中分类变量变为数值型的虚拟变量
X.head(2)#考察数据矩阵x的前两个观测值输出结果:
age campaign pdays previous emp.var.rate cons.price.idx cons.conf.idx euribor3m nr.employed job_admin. job_blue-collar job_entrepreneur job_housemaid job_management job_retired ... month_jul month_jun month_mar month_may month_nov month_oct month_sep day_of_week_fri day_of_week_mon day_of_week_thu day_of_week_tue day_of_week_wed poutcome_failure poutcome_nonexistent poutcome_success 0 30 2 999 0 -1.8 92.893 -46.2 1.313 5099.1 0 1 0 0 0 0 ... 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 39 4 999 0 1.1 93.994 -36.4 4.855 5191.0 0 0 0 0 0 0 ... 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 2 rows × 62 columns
y = bank.iloc[:, -1]#取出响应变量并赋值为y
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=1000, random_state=1)#将随机保留1000个观测值作为测试集,剩余用于训练集
(3)构建决策树
model = DecisionTreeClassifier(max_depth=2, random_state=123)#使用sklearnDecisionTreeClassifier类构造决策树
model.fit(X_train, y_train)#拟合决策树
model.score(X_test, y_test)#模型评价输出结果:
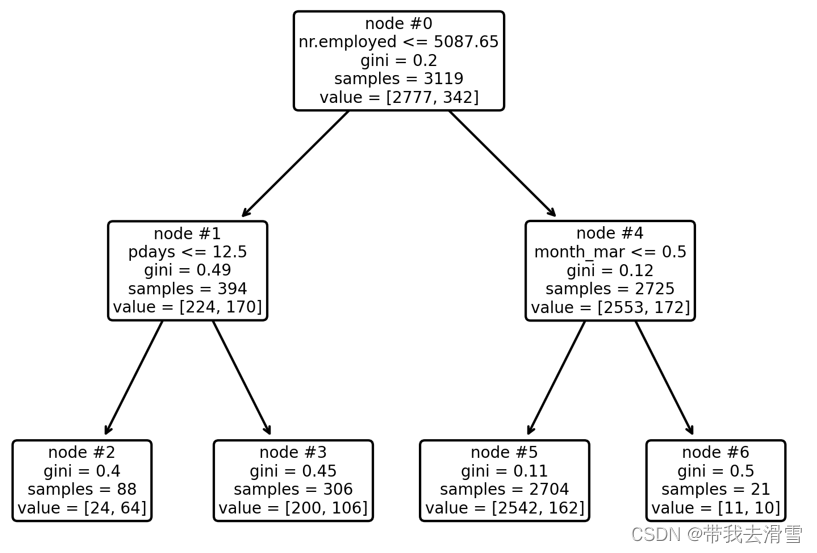
0.904plot_tree(model, feature_names=X.columns, node_ids=True, rounded=True, precision=2)#画出决策树
plt.savefig("squares0.png",
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
orientation ='landscape')输出结果:
结果显示,测试集的预测准确率达到90.4%。
(4)考察成本复杂性参数与叶节点总不纯度的关系
model = DecisionTreeClassifier(random_state=123)
path = model.cost_complexity_pruning_path(X_train, y_train)#得到一系列ccp_alpha值与相应叶节点总不纯度
plt.plot(path.ccp_alphas, path.impurities, marker='o', drawstyle='steps-post',color='pink')#画图展示二者之间的关系
plt.xlabel('alpha (cost-complexity parameter)')
plt.ylabel('Total Leaf Impurities')
plt.title('Total Leaf Impurities vs alpha for Training Set')
plt.savefig("squares1.png",
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
orientation ='landscape')输出结果:
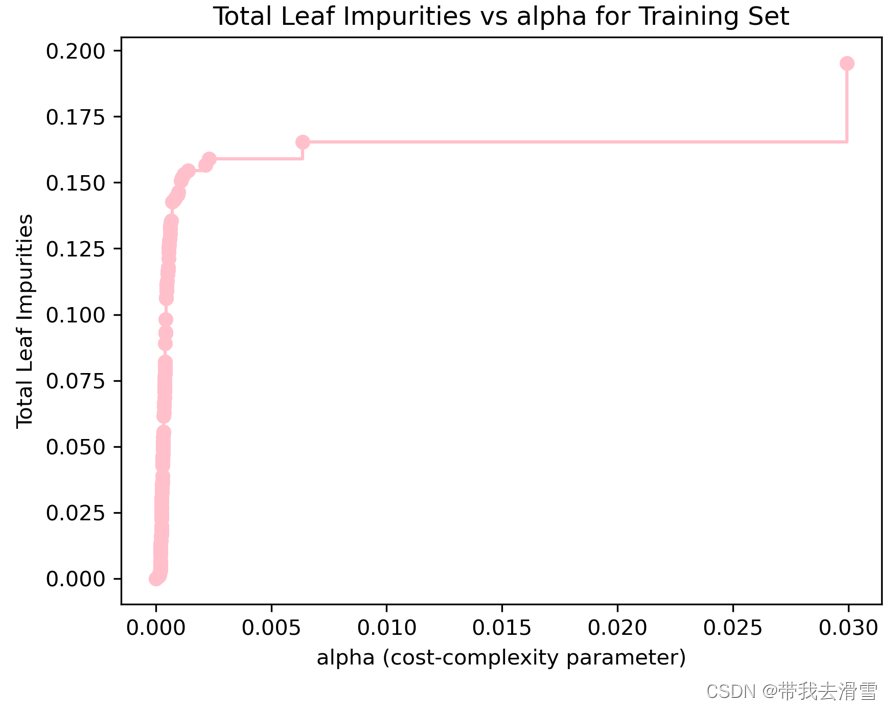
max(path.ccp_alphas), max(path.impurities)#寻找最大的ccp_alphas值与最大叶节点总不纯度值
输出结果:
(0.029949526543893212, 0.19525458100457016)
通过上图可以发现,当成本复杂性参数alpha为0时,并不惩罚决策树规模,导致每个观测值本身就为一个叶节点,总的叶节点的不纯度为0。当alpha上升时,对于决策树的惩罚力度增加,故叶节点总不纯度随之上升。当alpha的值约为0.02995时,决策树仅剩下树桩,叶节点总不纯度达到最大约为0.19525。
(5)通过10折交叉验证选择最优的超参数ccp_alpha值,并拟合模型
param_grid = {'ccp_alpha': path.ccp_alphas}#建立网格化
kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=1)#10折交叉验证选择最优超参数
model = GridSearchCV(DecisionTreeClassifier(random_state=123), param_grid, cv=kfold)
model.fit(X_train, y_train)
model.best_params_#获取最优超参数
model = model.best_estimator_#将模型重新定义为最优模型
model.score(X_test, y_test)#使用最优模型,计算测试集准确率
plot_tree(model, feature_names=X.columns, node_ids=True, impurity=True, proportion=True, rounded=True, precision=2)#proportion=True表示显示观测值的比重
plt.savefig("squares2.png",
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
orientation ='landscape')输出结果:
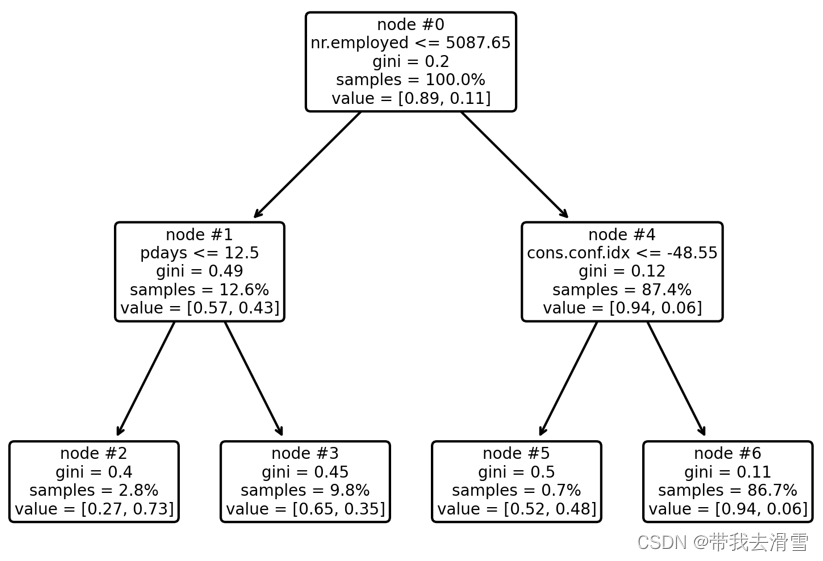
最优决策树解读:最优决策树只有4个终节点。其中根节点(node#0)拥有100%的样本数据,其中有购买意愿的有11%,没有购买意愿的为89%;从根节点出发,满足工作单位人数小于5088人的观测值进入左边的节点(node#1),反之进入右边的节点(node#4)。
节点node#1包含12.6%的样本数据,其中无购买意愿的比例为57%,而有购买意愿的比例为43%,从 节点node#1出发,满足条件自上次营销致电未过12.5天的观测值进入终结点node#2,反之进入node#3。在终节点node#2中有购买意愿的比例为73%,这意味着给当工作单位人数小于5088人且自上次营销致电未过12.5天的客户致电时,其购买存款理财产品的可能性最大。而node#3与node#5中有购买意愿的客户占比分别为35%、48%,也可以是致电的潜在客户人群。
(6)计算每个变量重要性并进行可视化
model.feature_importances_#计算每个变量的重要性值
sorted_index = model.feature_importances_.argsort()
plt.barh(range(X_train.shape[1]), model.feature_importances_[sorted_index])
plt.yticks(np.arange(X_train.shape[1]), X_train.columns[sorted_index])
plt.xlabel('Feature Importance')
plt.ylabel('Feature')
plt.title('Decision Tree')
plt.tight_layout()
plt.savefig("squares3.png",
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
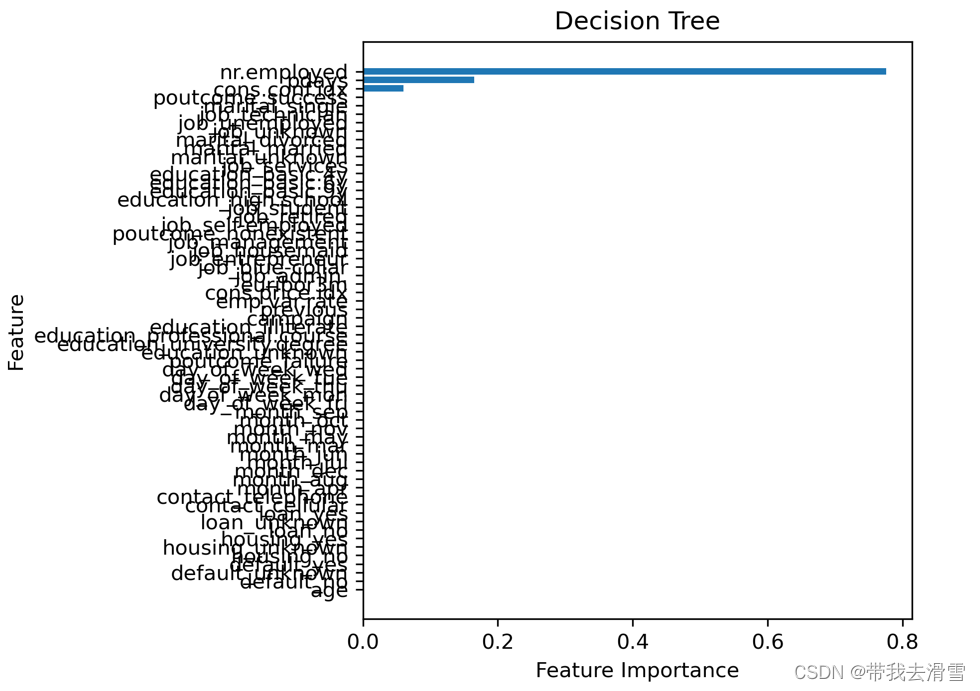
orientation ='landscape')输出结果:
结果显示,只有三个变量的重要性值不为0,其他变量的重要性值均为0,这是因为在分裂决策树时,没有用到这些变量。
(7)使用测试集进行预测,并计算混淆矩阵
pred = model.predict(X_test)#使用测试集进行预测
table = pd.crosstab(y_test, pred, rownames=['Actual'], colnames=['Predicted'])#展示混淆矩阵
table输出结果:
Predicted no yes Actual no 880 11 yes 85 24
(8)计算预测准确率与灵敏度、kappa指标
table = np.array(table)
Accuracy = (table[0, 0] + table[1, 1]) / np.sum(table)#计算预测准确率
Accuracy
输出结果:0.904Sensitivity = table[1, 1] / (table[1, 0] + table[1, 1])#计算灵敏度
Sensitivity输出结果:
0.22018348623853212cohen_kappa_score(y_test, pred)#计算kappa值
输出结果:
0.2960328518002493
结果显示虽然预测准确率达到90.4%,但决策树算法的灵敏度只有22%,即只能成功识别22%有购买意愿的客户。科恩的kappa指标值约为0.296,介于0.2至0.4区间,说明预测值与实际值的一致性一般。
(9)以0.1作为临界值重新进行预测,计算混淆矩阵与预测准确率、灵敏度
prob = model.predict_proba(X_test)%计算测试集中每位个体有购买意愿的概率
prob
model.classes_#确认第1列与第2列的类别,第1列为无购买意愿的,第2列为有购买意愿的
prob_yes = prob[:, 1]
pred_new = (prob_yes >= 0.1)#以0.1作为临界值
pred_new
table = pd.crosstab(y_test, pred_new, rownames=['Actual'], colnames=['Predicted'])
table
table = np.array(table)
Accuracy = (table[0, 0] + table[1, 1]) / np.sum(table)
Accuracy输出结果:
0.88 Sensitivity = table[1, 1] / (table[1, 0] + table[1, 1]) Sensitivity输出结果:
0.5412844036697247
结果显示,以0.1作为预测临界值,虽然预测准确率略有下降,但灵敏度却升高至54.1%。
2、回归决策树案例
使用波士顿房价数据集boston_housing_data.csv,该数据集有城镇人均犯罪率(CRIM)、住宅用地所占比例(ZN)、城镇中非住宅用地所占比例(INDUS)等共计13个特征变量,响应变量为社区房价中位数(MEDV)。
(1)导入数据与相应模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold, StratifiedKFold
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeRegressor,export_text
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.metrics import cohen_kappa_score
Boston=pd.read_csv(r"E:\工作\硕士\博客\博客28-分类决策树与回归决策树\boston_housing_data.csv")
Boston输出结果:
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PIRATIO B LSTAT MEDV 0 0.00632 18.0 2.31 0.0 0.538 6.575 65.2 4.0900 1 296.0 15.3 396.90 4.98 24.0 1 0.02731 0.0 7.07 0.0 0.469 6.421 78.9 4.9671 2 242.0 17.8 396.90 9.14 21.6 2 0.02729 0.0 7.07 0.0 0.469 7.185 61.1 4.9671 2 242.0 17.8 392.83 4.03 34.7 3 0.03237 0.0 2.18 0.0 0.458 6.998 45.8 6.0622 3 222.0 18.7 394.63 2.94 33.4 4 0.06905 0.0 2.18 0.0 0.458 7.147 54.2 6.0622 3 222.0 18.7 396.90 5.33 36.2 ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 501 0.06263 0.0 11.93 0.0 0.573 6.593 69.1 2.4786 1 273.0 21.0 391.99 9.67 22.4 502 0.04527 0.0 11.93 0.0 0.573 6.120 76.7 2.2875 1 273.0 21.0 396.90 9.08 20.6 503 0.06076 0.0 11.93 0.0 0.573 6.976 91.0 2.1675 1 273.0 21.0 396.90 5.64 23.9 504 0.10959 0.0 11.93 0.0 0.573 6.794 89.3 2.3889 1 273.0 21.0 393.45 6.48 22.0 505 0.04741 0.0 11.93 0.0 0.573 6.030 80.8 2.5050 1 273.0 21.0 396.90 7.88 11.9 506 rows × 14 columns
(2)划分训练集和测试集,构建决策树模型,并绘制决策树
data= Boston.iloc[:, :-1]#取出所有的特征变量,不含最后一列的响应变量
target=Boston.iloc[:, -1]#取出响应变量并赋值为target
Boston.feature_names=list(data.columns)#定义特征变量名称,方便后续绘制决策树
Boston.feature_names
X_train, X_test, y_train, y_test = train_test_split(data,target, test_size=0.3, random_state=0)#划分测试集和训练集
model = DecisionTreeRegressor(max_depth=2, random_state=123)#构建决策树
model.fit(X_train, y_train)#模型拟合
model.score(X_test, y_test)#求模型得分
print(export_text(model,feature_names=list(Boston.feature_names)))#输出决策树
plot_tree(model, feature_names=Boston.feature_names, node_ids=True, rounded=True, precision=2)#绘制决策树
plt.tight_layout()#将终节点在决策树中分开
plt.savefig("squares4.png",
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
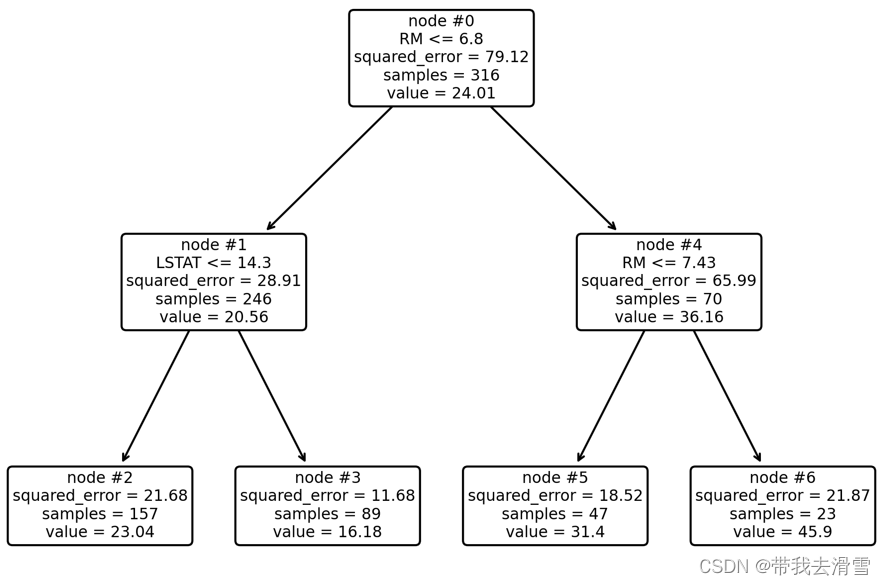
orientation ='landscape')输出结果:
(3)考察成本复杂性超参数与叶节点总均方误差的关系
model = DecisionTreeRegressor(random_state=123)
path = model.cost_complexity_pruning_path(X_train, y_train)
plt.plot(path.ccp_alphas, path.impurities, marker='o', drawstyle='steps-post',color='pink')
plt.xlabel('alpha (cost-complexity parameter)')
plt.ylabel('Total Leaf MSE')
plt.title('Total Leaf MSE vs alpha for Training Set')
plt.savefig("squares5.png",
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
orientation ='landscape')
max(path.ccp_alphas), max(path.impurities)输出结果:
(41.99790024501699, 79.12414356673514)
(4)通过10折交叉验证选择最优超参数alpha值,并以此构建决策树模型,绘制决策树
param_grid = {'ccp_alpha': path.ccp_alphas}
kfold = KFold(n_splits=10, shuffle=True, random_state=1)
model = GridSearchCV(DecisionTreeRegressor(random_state=123), param_grid, cv=kfold)
model.fit(X_train, y_train)
model.best_params_
model = model.best_estimator_
model.score(X_test,y_test)
plot_tree(model, feature_names=Boston.feature_names, node_ids=True, rounded=True, precision=2)
plt.tight_layout()
plt.savefig("squares6.png",
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
orientation ='landscape')输出结果:
(5)计算各变量的重要性值,并进行可视化
model.feature_importances_
sorted_index = model.feature_importances_.argsort()
X = pd.DataFrame(data, columns=Boston.feature_names)
plt.barh(range(X.shape[1]), model.feature_importances_[sorted_index],color='pink',edgecolor='red')
plt.yticks(np.arange(X.shape[1]), X.columns[sorted_index])
plt.xlabel('Feature Importance')
plt.ylabel('Feature')
plt.title('Decision Tree')
plt.tight_layout()
plt.savefig("squares7.png",
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
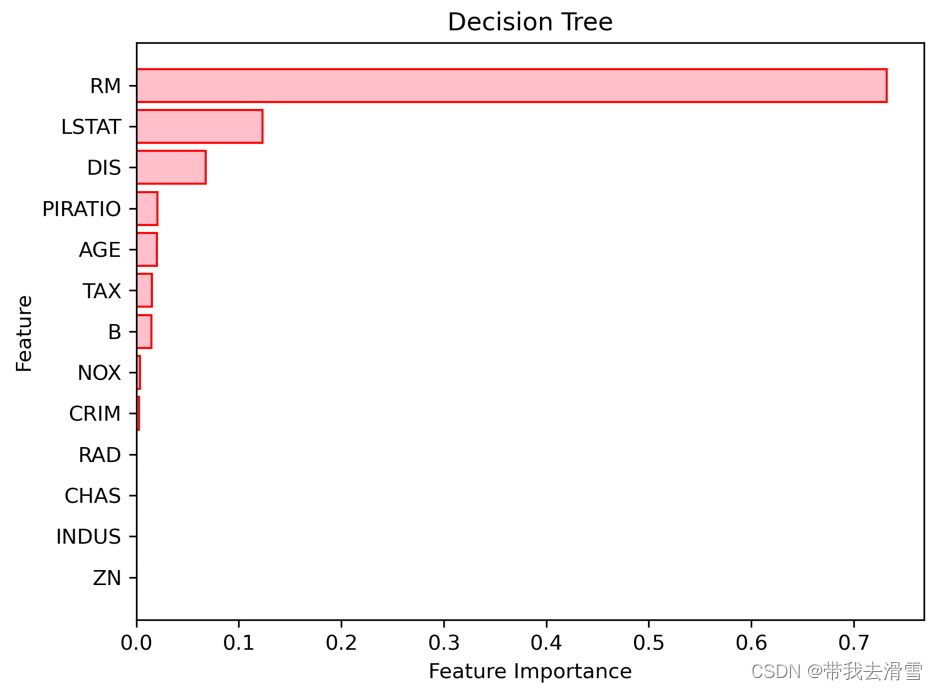
orientation ='landscape')输出结果:
可以发现,变量房间数(RM)最为重要,其次是低端人口比重(LSTAT),再次为犯罪率(CRIM),最后是离就业中心距离(DIS)与反映社区的生师比(PTRATIO)。
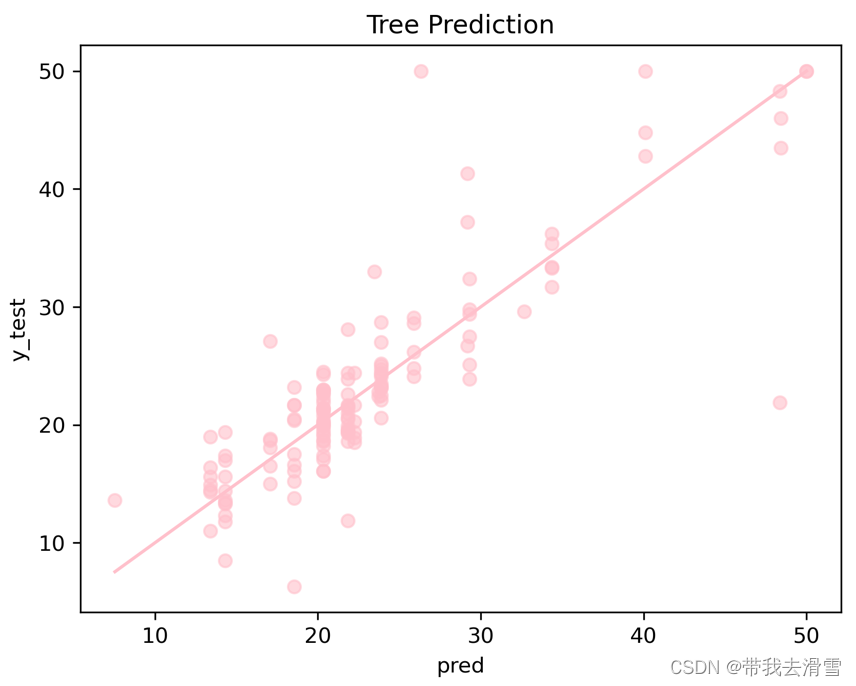
(6)使用测试集进行预测,画出预测值与实际值的散点图
pred = model.predict(X_test)
plt.scatter(pred, y_test, alpha=0.6,color='pink')
w = np.linspace(min(pred), max(pred), 100)
plt.plot(w, w,color='pink')
plt.xlabel('pred')
plt.ylabel('y_test')
plt.title('Tree Prediction')
plt.savefig("squares8.png",
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
orientation ='landscape')输出结果:
需要数据集的家人们可以去百度网盘(永久有效)获取:
链接:https://pan.baidu.com/s/173deLlgLYUz789M3KHYw-Q?pwd=0ly6
提取码:2138
更多优质内容持续发布中,请移步主页查看。
点赞+关注,下次不迷路!