🍑 算法题解专栏

---

🍑 [NOIP2000 提高组] 方格取数

题目描述

设有 $N\times N$ 的方格图 $(N\le 9)$，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字 $0$。如下图所示（见样例）:

A
 0  0  0  0  0  0  0  0
 0  0 13  0  0  6  0  0
 0  0  0  0  7  0  0  0
 0  0  0 14  0  0  0  0
 0 21  0  0  0  4  0  0
 0  0 15  0  0  0  0  0
 0 14  0  0  0  0  0  0
 0  0  0  0  0  0  0  0
                         B

某人从图的左上角的 $A$ 点出发，可以向下行走，也可以向右走，直到到达右下角的 $B$ 点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 $0$）。
此人从 $A$ 点到 $B$ 点共走两次，试找出 $2$ 条这样的路径，使得取得的数之和为最大。

输入格式

输入的第一行为一个整数 $N$（表示 $N\times N$ 的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的 $0$ 表示输入结束。

输出格式

只需输出一个整数，表示 $2$ 条路径上取得的最大的和。

样例 #1

样例输入 #1

8
2 3 13
2 6  6
3 5  7
4 4 14
5 2 21
5 6  4
6 3 15
7 2 14
0 0  0

样例输出 #1

67

👨‍🏫 大佬题解
👨‍🏫 局部最优 非 全局最优
👨‍🏫 个人最优 非 全体最优

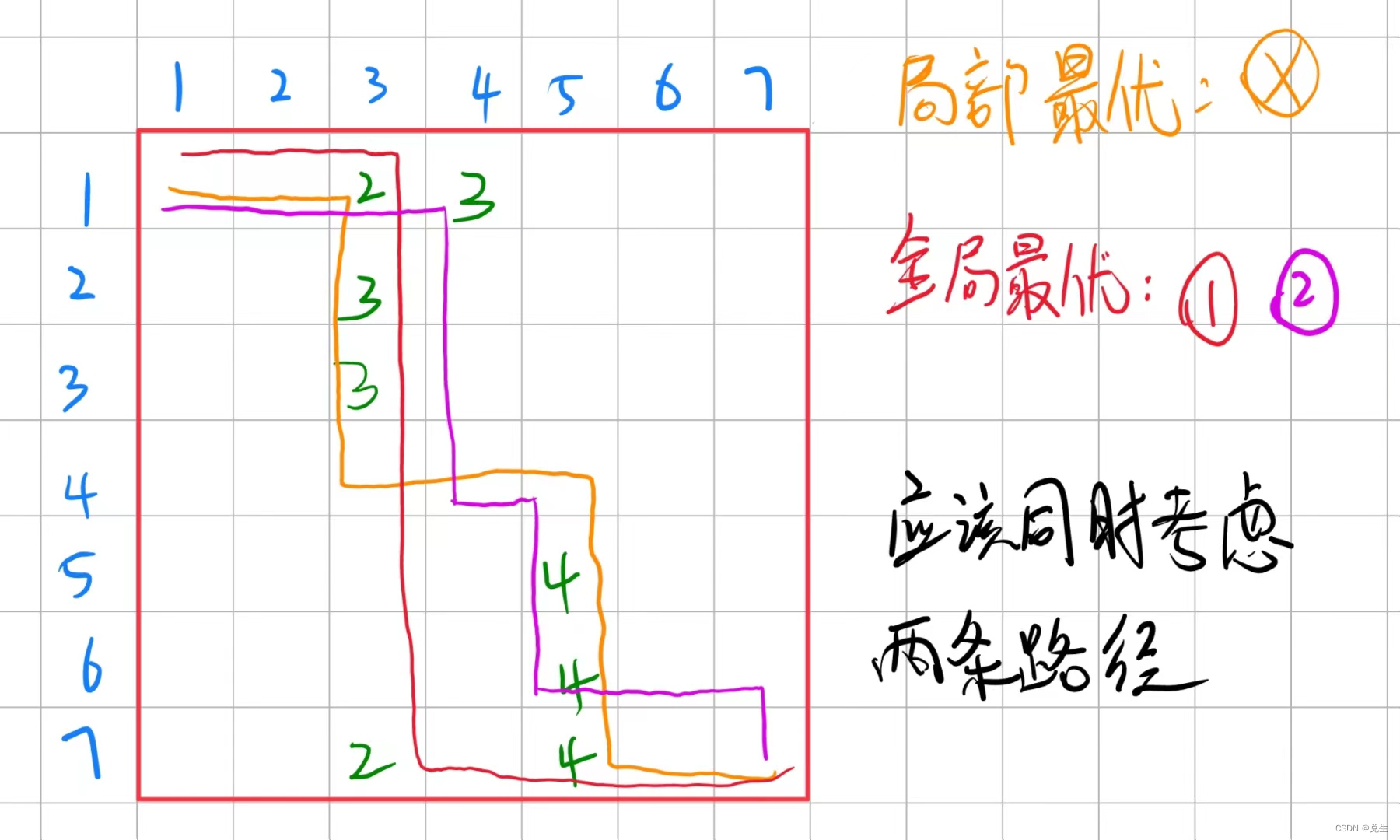
🍑 k 表示移动了多少路程（非位移），保证 两个路径 同时计算

import java.util.Scanner;

public class Main
{
	static int N = 11;
	static int[][] w = new int[N][N];
	static int[][][] f = new int[2 * N][N][N];

	public static void main(String[] args)
	{
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int a, b, c;
		while (sc.hasNext())
		{
			a = sc.nextInt();
			b = sc.nextInt();
			c = sc.nextInt();
			if (a == 0 && b == 0 && c == 0)
				break;
			w[a][b] = c;
		}

		for (int k = 2; k <= 2 * n; k++)//枚举路程
			for (int i1 = 1; i1 <= n; i1++)//枚举路径1的行
				for (int i2 = 1; i2 <= n; i2++)//枚举路径2的行
				{
					//
					int j1 = k - i1;
					int j2 = k - i2;
					if (j1 < 1 || j1 > n || j2 < 1 || j2 > n)
						continue;

					int t = w[i1][j1];
					if (i1 != i2)
						t += w[i2][j2];
//					两条路径都是从上边转移过来
					f[k][i1][i2] = Math.max(f[k][i1][i2], f[k - 1][i1 - 1][i2 - 1] + t);
//					1上  2左
					f[k][i1][i2] = Math.max(f[k][i1][i2], f[k - 1][i1 - 1][i2] + t);
//					1 左 2上
					f[k][i1][i2] = Math.max(f[k][i1][i2], f[k - 1][i1][i2 - 1] + t);
//					1 左 2左
					f[k][i1][i2] = Math.max(f[k][i1][i2], f[k - 1][i1][i2] + t);

				}
		System.out.println(f[2 * n][n][n]);
	}
}