1. 题目介绍（Decode Ways）

A message containing letters from A-Z can be encoded into numbers using the following mapping:

【Translate】： 包含从A到z的字母的消息可以使用以下映射编码为数字

‘A’ -> “1”
‘B’ -> “2”
…
‘Z’ -> “26”

To decode an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, “11106” can be mapped into:

【Translate】： 要解码已编码的信息，必须将所有数字分组，然后使用上述映射的相反方法(可能有多种方法)映射回字母。例如，“11106”可以映射为

“AAJF” with the grouping (1 1 10 6)
“KJF” with the grouping (11 10 6)

Note that the grouping (1 11 06) is invalid because “06” cannot be mapped into ‘F’ since “6” is different from “06”.

【Translate】： 注意分组(1 11 06)是无效的，因为“06”不能映射到“F”，因为“6”与“06”不同。

Given a string s containing only digits, return the number of ways to decode it.

【Translate】： 给定一个只包含数字的字符串s，返回解码方法的数量。

The test cases are generated so that the answer fits in a 32-bit integer.

【测试用例】：

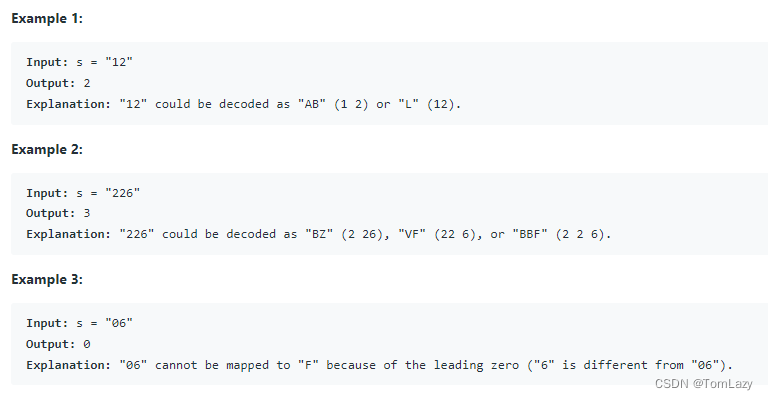
testcase

【条件约束】：

Constraints

2. 题解

以下原题解均来自于 yu6 的 Evolve from recursion to dp.

2.1 递归

递归O (2ⁿ)，一个字符可以单独解码，也可以与下一个字符配对解码。

class Solution {
	public int numDecodings(String s) {
        return s.length()==0?0:numDecodings(0,s);      
    }
    private int numDecodings(int p, String s) {
        int n=s.length();
        if(p==n) return 1;
        if(s.charAt(p)=='0') return 0;
        int res=numDecodings(p+1,s);
        if(p<n-1&&(s.charAt(p)=='1'||s.charAt(p)=='2'&&s.charAt(p+1)<'7')) 
			res+=numDecodings(p+2,s);
        return res;
    }
}

act1

2.2 递归+记忆数组

时间复杂度：O(n).

class Solution {
	public int numDecodings(String s) {
        int n=s.length();
        Integer[] mem=new Integer[n];
        return s.length()==0?0:numDecodings(0,s,mem);      
    }
    private int numDecodings(int p, String s, Integer[] mem) {
        int n=s.length();
        if(p==n) return 1;
        if(s.charAt(p)=='0') return 0;
        if(mem[p]!=null) return mem[p];
        int res=numDecodings(p+1,s,mem);
        if(p<n-1&&(s.charAt(p)=='1'||s.charAt(p)=='2'&&s.charAt(p+1)<'7')) 
			res+=numDecodings(p+2,s,mem);
        return mem[p]=res;
    }
}

act2

2.3 动态规划

O(n)的时间和空间.

class Solution {
	public int numDecodings(String s) {
        int n=s.length();
        int[] dp=new int[n+1];
        dp[n]=1;
        for(int i=n-1;i>=0;i--)
            if(s.charAt(i)!='0') {
                dp[i]=dp[i+1];
                if(i<n-1&&(s.charAt(i)=='1'||s.charAt(i)=='2'&&s.charAt(i+1)<'7')) 
					dp[i]+=dp[i+2];
            }
        return dp[0];   
    }
}

act3

2.4 常数空间下的动态规划

class Solution {
	public int numDecodings(String s) {
        int dp1=1, dp2=0, n=s.length();
        for(int i=n-1;i>=0;i--) {
            int dp=s.charAt(i)=='0'?0:dp1;
            if(i<n-1&&(s.charAt(i)=='1'||s.charAt(i)=='2'&&s.charAt(i+1)<'7'))
                dp+=dp2;
            dp2=dp1;
            dp1=dp;
        }
        return dp1;
    }
}