121. 买卖股票的最佳时机

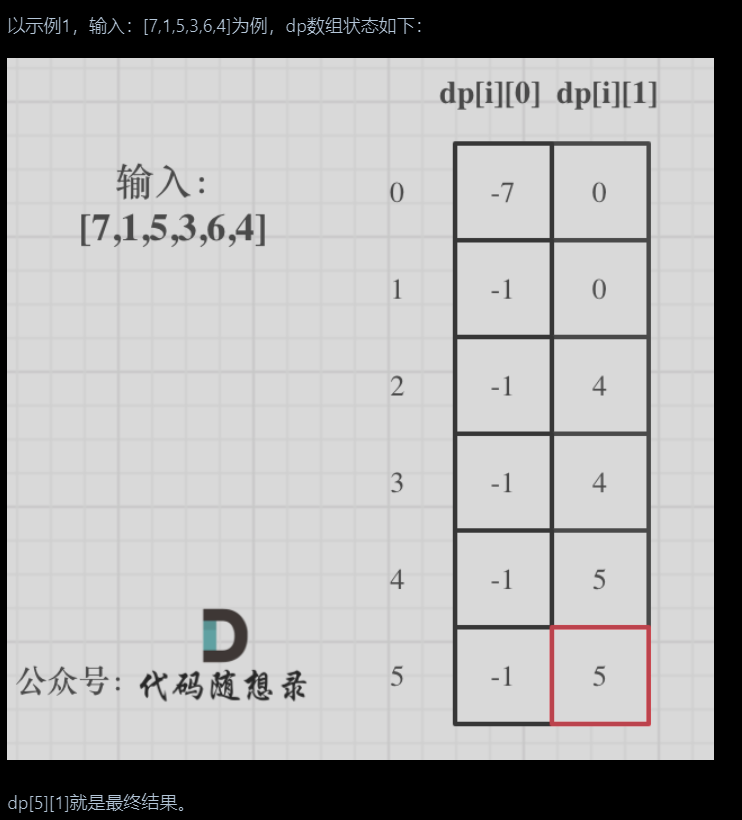
为什么定义dp数组为二维数组？
dp数组定义，dp(i)[0] 表示第i天持有股票所得最多现金，dp(i)[1]表示第i天不持有股票的状态（未必当前卖出）
这样定义可以表示所有状态，否则dp[i]表示买入，那还要定义第i天卖出，和剩下两种状态持有和不持有

• 题目链接：代码随想录

• 解题思路：
  ①dp数组,dp(i)[0]表示第i天持有股票的最大现金，dp(i)[1]表示第i天不持有股票的最大现金
  ②递推公式

  ​ 1.第i天持有股票，可能第i天没买，最大现金为前一天持有股票的最大状态；有可能第i天买了，而且一定是第一次买，所以为-price[i]
  ​ 2.第i天不持有股票**，可能是第i - 1天就不持有状态顺延；也有可能是正好这一天卖出股票，所以总现金为前一天持有状态 + 今天卖出状态
  ​ ③初始化：
  ​ 因为要用到i - 1状态，所以要有第0个元素
  ​ ④遍历顺序：从前向后，因为后状态依赖前状态

• 推导过程

  

public int maxProfit(int[] prices) {
    //dp数组
    //dp[i][0]表示第i天持有股票的最大现金，dp[i][0]表示第i天不持有股票的最大现金
    int[][] dp = new int[prices.length][2];
    //初始化
    //因为i - 1所以，要有第0个元素
    dp[0][0] = -prices[0];
    dp[0][1] = 0;
    //遍历
    for (int i = 1; i < prices.length; i++) {
        //第i天持有股票，可能第i天没买，最大现金为前一天持有股票的最大状态；有可能第i天买了，而且一定是第一次买，所以为-price[i]
        dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);
        //第i天不持有股票，可能是第i - 1天就不持有状态顺延；也有可能是正好这一天卖出股票，所以总现金为前一天持有状态 + 今天卖出状态
        dp[i][1] = Math.max(dp[i - 1][1],dp[i - 1][0] + prices[i]);
    }
    //一定是第i天不持有股票现金多,不持有一定现金更多
    return dp[prices.length - 1][1];
}

122.买卖股票的最佳时机II

本题和上一题唯一的区别在于：
当第i天持有并且第i天买入的情况，不再是单纯的-了，而是要算上前一天不持有的状态，因为可以买卖多次
而第i天不持有的情况和之前状态一样

• 题目链接：代码随想录

public int maxProfit(int[] prices) {
    //dp数组
    int[][] dp = new int[prices.length][2];
    //初始化
    dp[0][0] = -prices[0];
    dp[0][1] = 0;
    //遍历
    for (int i = 1; i < prices.length; i++) {
        //第i天持有股票，当第i天买入的时候，不再是单纯的-了，而是要算上前一天不持有的状态，因为可以买卖多次
        dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
        //第i天不持有股票，状态和只能买卖一次的状态一样
        dp[i][1] = Math.max(dp[i - 1][1],dp[i - 1][0] + prices[i]);
    }
    //一定是第i天不持有股票现金多,不持有一定现金更多
    return dp[prices.length - 1][1];
}