“五一”小长假来了趟上海,在倒数第二天终于有时间做了一会儿题目,A了之后过来写一篇题解
【问题描述】
农民约翰雇一个专业摄影师给他的部分牛拍照。由于约翰的牛有好多品种,他喜欢他的照片包含每个品种的至少一头牛。
约翰的牛都站在一条沿线的不同地方, 每一头牛由一个整数位置 X_i以及整数品种编号 ID_i表示。
约翰想拍一张照片,这照片由沿线的奶牛的连续范围组成。照片的成本与规模相当,这就意味着,在一系列照片中的最大和最小 X 坐标的差距决定了照片的成本。
请帮助约翰计算最小的照片成本,这些照片中有每个不同的品种的至少一头牛,没有两头牛愿意站在同一个地点的。
【输入格式】
第 1 行:牛的数量 N;
第 2..1+N 行:每行包含 2 个以空格分隔的正整数 X_i 和 ID_i;意义如题目描述;
【输出格式】
输出共一行,包含每个不同品种 ID 的照片的最低成本。
输入 #1
6
25 7
26 1
15 1
22 3
20 1
30 1 输出 #1
4 --------------------------------------------------------------------------------------------------------------------------------
这题是我在学完单调队列、单调栈之后教练留的题目,但是我根本没用这两种(自己都觉得神奇)
题目说了每个牛有自己的位置和品种,想要照一张照片,照片必须涵盖所有品种的奶牛至少一头,然后照片长度还需要最短
也就是说:每个品种的奶牛都要尽量缩减数量
首先先把这些奶牛按照坐标升序排序,不然会很乱
题目中提示你:最大和最小 X 坐标的差距决定了照片的成本
只需要计算出最小的坐标和最大的坐标即可
算法整体大框架:
用两个变量表示现在的最小最大的坐标,分别命名为head,tail
因为我们要尽量减少每一种奶牛的数量,所以head和tail位置一定要是目前数量为1的牛,而head 和tail之间的🐮就管不了了
(macbook都没个像样的自带画图软件只能将就了
栗子🌰:
位置:1 2 3 5 8 10
品种:5 5 2 2 3 3
head tail初始head为1,tail为n
首先,head位置和旁边都是5,既然要保留最少的个数,就把head++,吞掉第一个
目前,5品种的🐮只剩这一只了,不能再删了
来看tail这边,他旁边的和他是一个品种,只能无情把这个🐮删掉了,tail--
整个过程就是这样的,就是前后一直缩减,直到head和tail位置品种的🐮都是一个为止
把这些抽象成代码就很简单了:
注意⚠️:先缩减head和先缩减tail的结果也许是不一样的,所以得计算两次,最后取最小值
# include <iostream>
# include <cstdio>
# include <deque>
# include <algorithm>
# include <map>
using namespace std;
# define int long long
int n,head,tail;
struct node{
int x,d;
}a[60005];
bool cmp(node a,node b){
return a.x<b.x;
}
map <int,int> v;
map <int ,int> v1;
signed main(){
scanf("%lld",&n);
for (int i=1;i<=n;i++){
scanf("%lld%lld",&a[i].x,&a[i].d);
v[a[i].d]++;
v1[a[i].d]++;
}
sort(a+1,a+1+n,cmp);
head=1,tail=n;
int first=0,second=0;
while(v[a[tail].d]!=1){
v[a[tail].d]-=1;
tail--;
}
while(v[a[head].d]!=1){
v[a[head].d]-=1;
head++;
}
first=a[tail].x-a[head].x;
head=1,tail=n;
while(v1[a[head].d]!=1){
v1[a[head].d]--;
head++;
}
while(v1[a[tail].d]!=1){
v1[a[tail].d]--;
tail--;
}
second=a[tail].x-a[head].x;
printf("%lld",min(first,second));
return 0;
}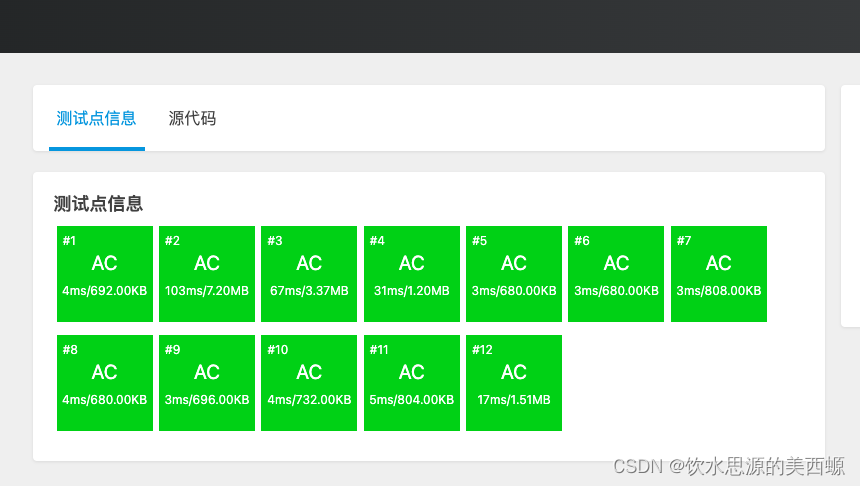
一道提高+的题就AC掉力,没用单调队列和单调栈也能完美解决
今天的讲解就到这里,下次再见!
(完结撒花!🎉
![[MAUI]模仿iOS应用多任务切换卡片滑动的交互实现](https://img-blog.csdnimg.cn/6fca7de1f85646dc894e72f43390f317.gif)





![[网络原理] HTTP协议](https://img-blog.csdnimg.cn/0165697193564bd7ae9aefb62d133e0a.png)