大部分人在学习编程时接触的第一个算法应该就是递归了,递归的思想其实很好理解,就是将一个问题拆分为若干个与本身相似的子问题,通过不断调用自身来求解。
但很多新手在实际操作中却很难正确使用到递归,有时面对问题还会有种无从下手的感觉,在此,我总结了一些解决递归问题的方法和思路,希望对你能有所帮助。
1.什么是递归
递归简单来说就是在运行过程中不断调用自己,直到碰到终止条件,返回结果的过程。
递归可以看作两个过程,分别是递和归。递就是原问题把要计算的结果传给子问题;归则是子问题求出结果后,把结果层层返回原问题的过程。
下面设一个需要经过三次递归的问题,为大家详细看一下递归的过程:
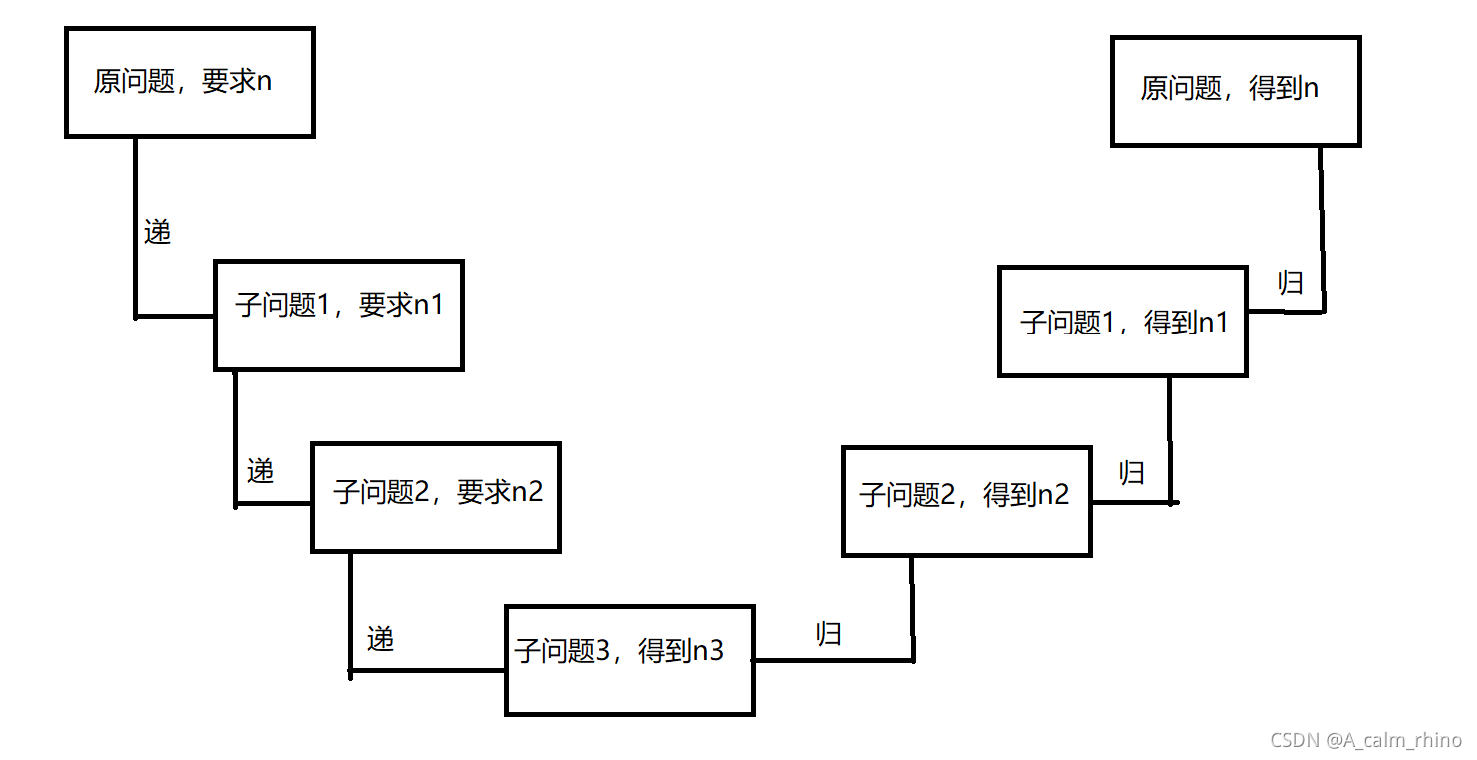
当然,现实中我们遇到递归问题是不会按照图中一样一步一步想下来,主要还是要掌握递归的思想,找到每个问题中的规律。
2.什么时候使用递归
递归算法无外乎就是以下三点:
1.大问题可以拆分为若干小问题
2.原问题与子问题除数据规模不同,求解思路完全相同
3.存在递归终止条件
而在实际面对递归问题时,我们还需要考虑第四点:当不满足终止条件时,要如何缩小函数值并让其进入下一层循环中
3.递归的实际运用(阶层计算)
了解了大概的思路,现在就要开始实战了。下面我们来看一道经典例题:
求N的阶层。
首先按照思路分析是否可以使用递归算法:
- N!可以拆分为(N-1)!*N
- (N-1)!与N!只有数字规模不同,求解思路相同
- 当N=1时,结果为1,递归终止
满足条件,可以递归:
public static int Factorial(int num)
{
if(num==1)
{
return num;
}
return num*Factorial(num-1);
}
而最后的return,便是第四步,缩小参数num的值,让递归进入下一层。
一般来说,第四步往往是最难的,需要弄清该如何缩小范围,如何操作返回的数值,这一步只能通过不断地练习提高了(当然如果你知道问题的数学规律也是可以试出来的)。
4.其它递归例题:
一:顺序打印,当输入一个整数时,按顺序依次打印每一位的值
该题可以理解为不断拆分整数的最大位,并将它们一一打印。与求阶层不同的是,该题的递归是在终止条件里进行的。
令num不断除10,最后只剩下最高位时并打印。
而在输出时%10,是因为当最高位打印返回后,继续打印的数不一定是个位数,%10只保留个位。
public static void PrintNumber(int num)
{
if (num>10)
{
PrintNumber(num/10);
}
System.out.print(num%10+",");
}
二:斐波那契数列:有一个数列:1、1、2、3、5、8、13、21、34…,求该数列的第 n 项的值是多少。
有了以上两个例子,这样的递归问题就很好解决了。
首先我们观察斐波那契数列的规律是N=(N-1)+(N-2),要保证返回值不为0,所以有两个终止条件。
public static int Fibonacci(int num)
{
if (num==1||num==2)
{
return 1;
}
return Fibonacci(num-1)+Fibonacci(num-2);
}
之后让我们再来看看递归的应用问题,与数学问题相比,在做应用题前需要先将题转换为数学问题,找到规律后再进行代码编写。
三 :汉诺塔(Tower of Hanoi)源于印度传说中一个古老的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
汉诺塔问题算是递归算法的经典例题了,很多初学者的入门题就是它。
在刚看到汉诺塔的时候,相信很多人都是一头雾水,不知道如何下手。其实面对应用题的时候,先建立它的模型,弄清题意后,再寻找其中的数学规律,解题思路便会清晰不少。
1.首先,题目的意思就是一个柱子A上有64的按大小顺序放置的圆片,要全部移动到另一根柱子C上,每次只能移动一个,可以借助柱子B,且小的不能在大的下面。求最少的移动次数。
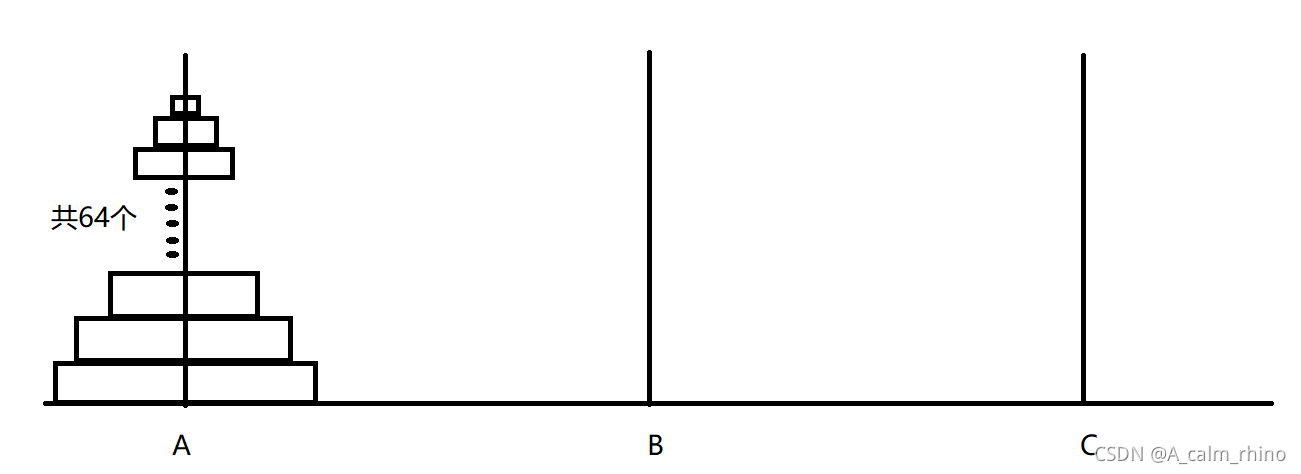
2.然后,寻找其中的数学规律(数学归纳法)。
先让所有圆片从上到下按1到N排序。
当N=1时,只需从A->C,移动1次。
当N=2时,先让1号从A->B,再让2号从A->C,最后让1号从B->C,移动3次。
当N=3时,可以理解为先让1、2号从A->B,再让3号从A->C,最后让1、2号从B->C。因为由N=2可以得知,移动两片需要3次,而A->B,B->C共进行了两次,所以共有6次,再加上3号A->C的过程,要移动7次。
同理,当N=4时,共要移动2×7(N=3的移动次数)+1=15次。
…
所以,当N=N时,要移动2×(N-1)的移动次数+1次
(其实也可以看做2的N次方-1)
至此,得到了该题的规律,代码便好些多了。
public static int TowerOfHanoi(int num)
{
if (num==1)
{
return 1;
}
return TowerOfHanoi(num-1)*2+1;
}
四:青蛙跳台阶问题:一只青蛙一次可以跳1级或2级台阶,求该青蛙跳N级的台阶总共有多少种跳法。
有了汉诺塔的经验,这道题做起来就很顺利了
先分析题意,再总结数学规律(本题题意简单,就直接开始数学归纳了)
当N=1,1种跳法。
当N=2,2种跳法。
当N=3,青蛙第一次跳的时候,它只有两种选择:跳1级,剩两级台阶,即N=2,有2种跳法;跳2级,剩一级台阶,即N=1,1种跳法。 所以,N3的跳法=N2+N1。
所以,N4=N3+N2
…
其实现在你一定会发现,青蛙跳台阶问题和斐波那契额数列的数学规律是一样的,分析清楚之后,代码也就写出来了:
public static int FrogJumpSteps(int num)
{
if (num==1)
{
return 1;
}
if (num==2)
{
return 2;
}
return FrogJumpSteps(num-1)+FrogJumpSteps(num-2);
}
5.总结
到此,基本把递归算法的基础为大家讲了一遍。当然,我说的只是最基础的部分,递归算法在之后还有很多变式,如:如何避免重复运算,如何自下而上操作等等。
最后,祝大家在编程的道路上越走越远。
大鹏一日同风起,扶摇直上九万里。