全部代码
全部代码在github acwing 上
正在更新
https://github.com/stolendance/acwing
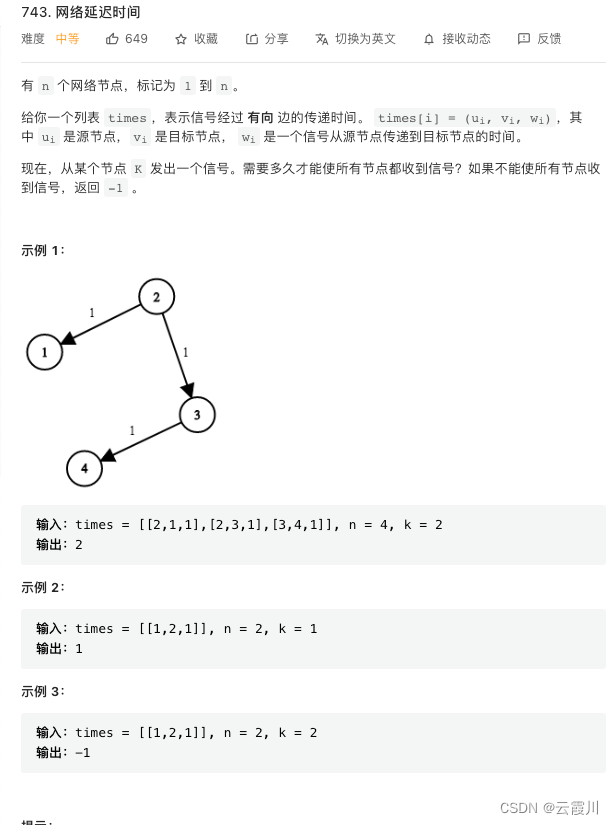
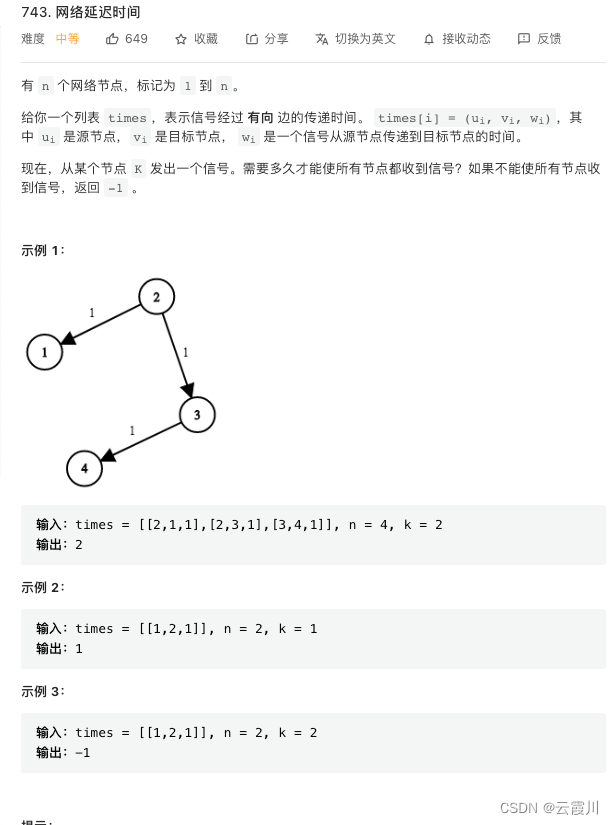
图论
欢迎大家star与fork
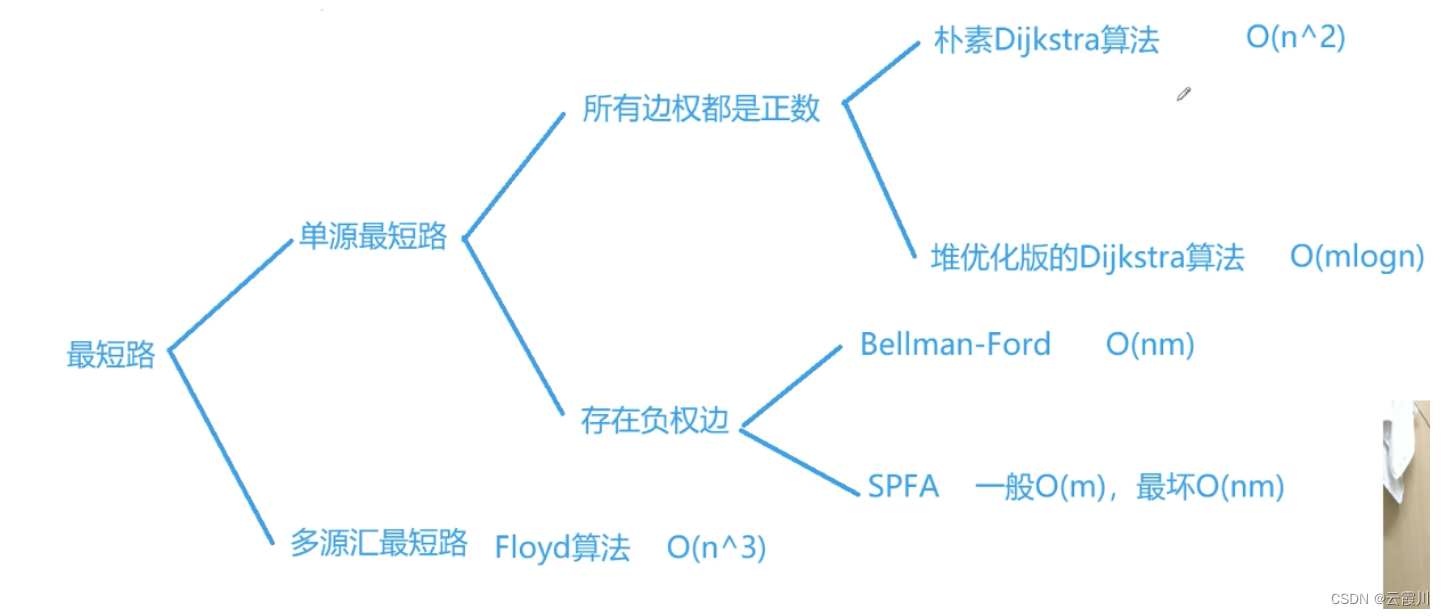
单源最短路问题 先用spfa算法 不行再换其他的
spfa-超级万能 说不定比dijsktra还快
dis[] 代表第k到某一点的最短距离
queue 代表刚被更新的点 它有可能更新其他路径 所以检查它的出边
isin代表该点是否在queue中
队列放入起点 <-k
while(队列不为空)
取出队头
遍历所有t的出边 t-w>b
如果dis[b]>dis[t]+w[t,b],更新,如果b不在队列中,加入b
typedef long long ll;
typedef pair<ll,ll> pll;
struct Edge
{
int next;
int val;
Edge(int next_,int val_):next(next_),val(val_){;}
};
class Solution {
public:
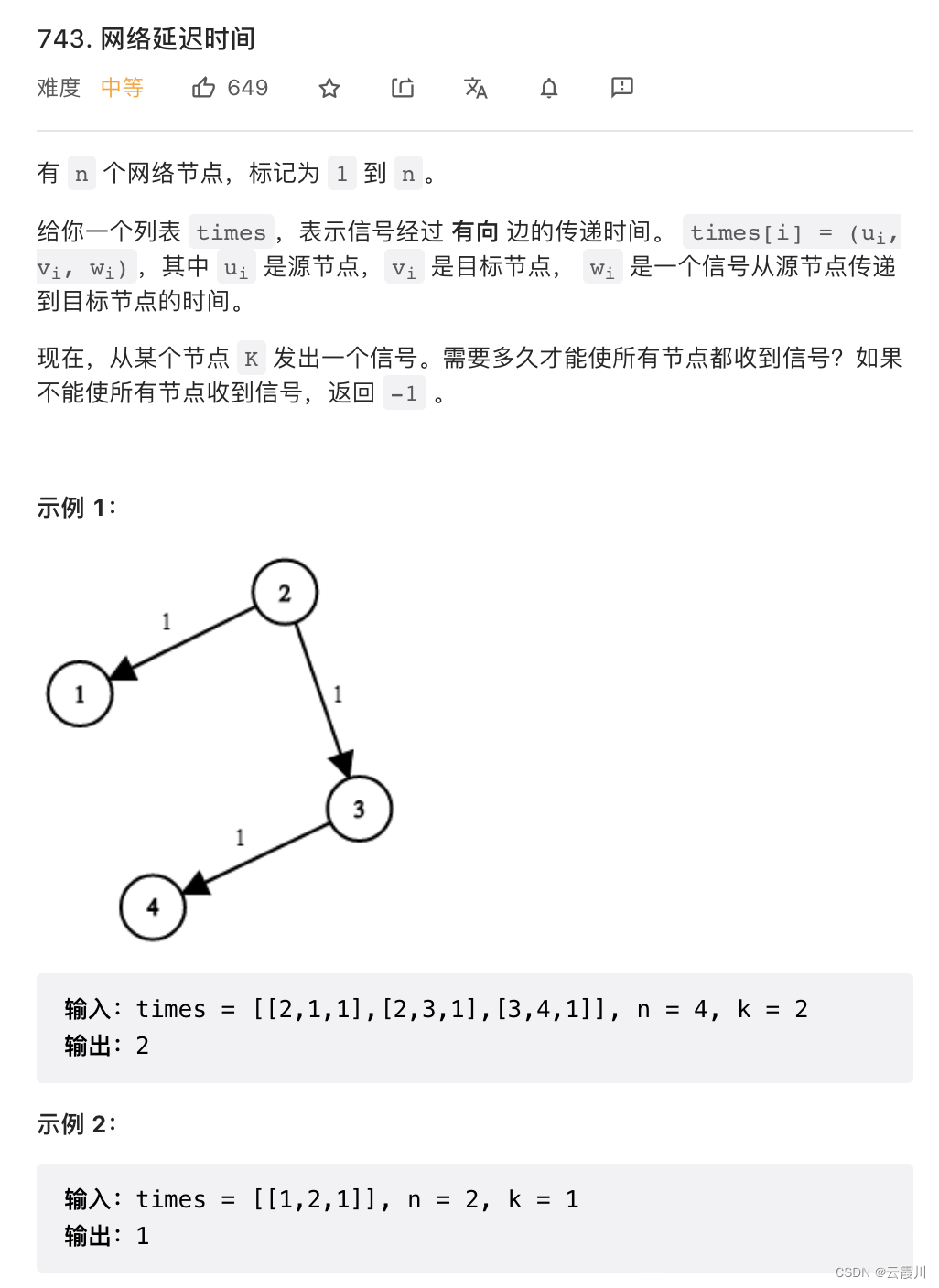
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
vector<vector<Edge> > graph(n+1);
for(auto item:times)
{
int a=item[0];
int b=item[1];
int c=item[2];
graph[a].push_back(Edge(b,c));
}
vector<ll> dis(graph.size(),INT_MAX);
vector<int> isin(graph.size(),0);
queue<int> ls;
ls.push(k);
dis[k]=0;
isin[k]=1;
while(ls.size())
{
int t=ls.front();
ls.pop();
isin[t]=0;
for(int i=0;i<graph[t].size();i++)
{
// k->t->id
int distance=graph[t][i].val;
int id=graph[t][i].next;
if(dis[t]+distance<dis[id]){
dis[id]=dis[t]+distance;
if(isin[id]==0)
{
ls.push(id);
isin[id]=1;
}
}
}
}
int rs= *max_element(dis.begin()+1,dis.end());
if(rs==INT_MAX) return -1;
else return rs;
}
};
朴素版dijsktra -单源最短路-所有边权重都是正数 基于 稠密图(邻接矩阵)
s:当前已经确定最短路径距离的点
-
dis[0 ]=0 dis[i]=+OO 只有起点被确定到了
-
for(i 1 …n)
t《- 不在s中的距离最近的点
s〈-t
用t更新其他点的距离(看下)
dij实现的时候是通过 将距离设置成无穷大 来表达 不可达
dij 由于边很多, 稠密图 所以用邻接矩阵存即可
dij 需要找n个点 所以外层是一个for循环x
总结下来:
1. 把未加入的最近的加进来
2. 标记加入
3. 根据加入的点更新距离
#include<iostream>
#include<vector>
using namespace std;
#define INA INT_MAX
//https://leetcode.cn/problems/network-delay-time/
int networkDelayTime(vector<vector<int> >& times, int N, int k) {
// 因为点的坐标是从1开始 , 所以开N+1个
// 直接在graph上更新 方便很多
// graph要采用long long INT_MAX+某个数 不会变成负数
vector<vector<long long> > graph(N+1,vector<long long>(N+1,INT_MAX));
for(int i=1;i<=N;i++) graph[i][i]=0;
for(auto e:times) graph[e[0]][e[1]]=e[2];
vector<int> vis(graph.size(),0);
vis[k]=1;
// 只要找下除了起点的接下来的点
for(int i=1;i<graph.size()-1;i++)
{
int minid=0,minx=INA;
// 在没有使用过的检查最短的距离
for(int j=1;j<graph.size();j++)
{
if(vis[j]==0&&graph[k][j]<minx)
{
minid=j;
minx=graph[k][j];
}
}
vis[minid]=1;
// 更新
// 根据这个点更新其他所有距离
for(int j=1;j<graph.size();j++)
{
graph[k][j]=min(graph[k][j],graph[k][minid]+ graph[minid][j]);
}
}
int ans=0;
for(int i=1;i< graph.size();i++)
{
if(graph[k][i]==INT_MAX) return -1;
ans=max(ans, (int)graph[k][i]);
}
return ans;
}
int main()
{
vector<vector<int> > times={{2,1,1},{2,3,1},{3,4,1}};
int rs=networkDelayTime(times,4,2);
cout<<rs<<endl;
}
dijstra 稀疏图(邻接表) -我更喜欢的方式!!!
求点k到其他点的距离
与上面不同的情况是, 采用邻接表+最小堆
最小堆 的格式是(点k到该点的距离,该点的id)
dis[] 存储的是点k到达每个点的最短距离
st[] 存储的是否能确定点k到达每个点的距离
while(队列不为空)
{
队列弹出一个
如果该点确定了最短距离,就不管它 if(st[]) continue
把弹出的这个点加入最短距离
根据这个点进行扩展,遍历这个点指向其他点的边
如果比div小,则更新距离
加入队列中
}

typedef long long ll;
typedef pair<ll,ll> pll;
struct Edge
{
int next;
int val;
Edge(int next_,int val_):next(next_),val(val_){;}
};
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
vector<vector<Edge> > graph(n+1);
for(auto item:times)
{
int a=item[0];
int b=item[1];
int c=item[2];
graph[a].push_back(Edge(b,c));
}
vector<ll> dis(graph.size(),INT_MAX);
vector<int> st(graph.size(),0);
priority_queue<pll,vector<pll>,greater<pll> > ls;
ls.push(pll(0,k));
dis[k]=0;
while(ls.size())
{
auto item=ls.top();
ls.pop();
ll distance=item.first;
int id=item.second;
// 保证未加入
if(st[id]) continue;
// 加入
st[id]=1;
// 扩展更新
for(int i=0;i<graph[id].size();i++)
{
// k->id->id2
// distance distance2
int id2=graph[id][i].next;
int distance2=graph[id][i].val;
if(distance+distance2<dis[id2])
{
dis[id2]=distance+distance2;
// 加入队列
ls.push(pll(dis[id2],id2));
}
}
}
int rs=(int)*max_element(dis.begin()+1,dis.end());
if(rs==INT_MAX) return -1;
else return rs;
}
};