Problem - E - Codeforces

有人给Ivan一个奇怪的生日礼物,这是一只刺猬 - 一个连通的无向图,其中一个顶点的度至少为3(我们称其为中心),而所有其他顶点的度数均为1。Ivan认为刺猬太无聊了,决定自己制造k-多刺猬。
我们将k-多刺猬定义如下:
1-多刺猬是刺猬:它有一个度至少为3的顶点和一些度为1的顶点。 对于所有k≥2,k-多刺猬是(k-1)-多刺猬,在每个度数为1的顶点v上进行以下更改:令u为它唯一的邻居;删除顶点v,创建一个以顶点w为中心的新刺猬,并用一条边连接顶点u和w。新的刺猬可以彼此不同,也可以与初始礼物不同。 因此,k-多刺猬是一棵树。Ivan制作了k-多刺猬,但他不确定是否没有犯任何错误。这就是为什么他要求你检查他的树是否确实是k-多刺猬。
输入: 第一行包含两个整数n和k(1≤n≤105,1≤k≤109)——顶点数和刺猬参数。
接下来的n-1行,每行包含两个整数u和v(1≤u,v≤n;u≠v)——相连的边的顶点索引。
保证给定的图是一棵树。
输出: 如果给定的图是k-多刺猬,则打印"Yes"(不带引号),否则打印"No"(不带引号)。
Examples
input
Copy
14 2 1 4 2 4 3 4 4 13 10 5 11 5 12 5 14 5 5 13 6 7 8 6 13 6 9 6
output
Copy
Yes
input
Copy
3 1 1 3 2 3
output
Copy
No
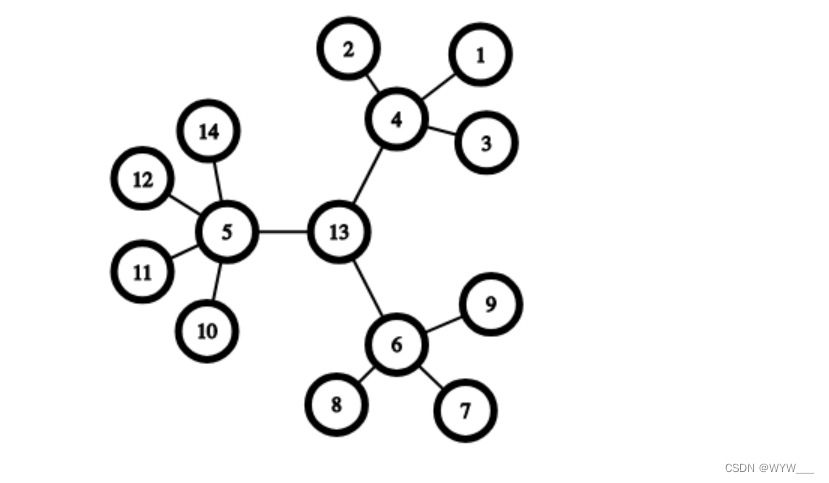
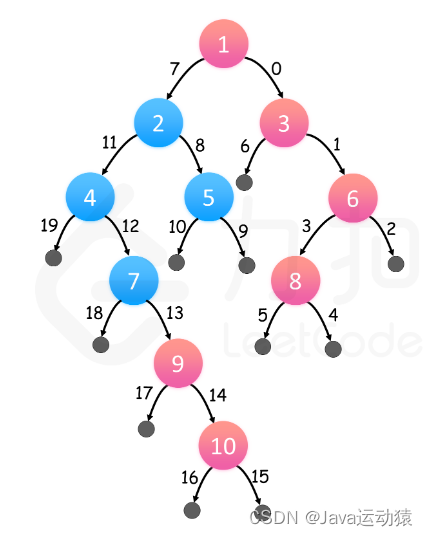
第一个例子中的2-Multihedgehog如下所示:
它的中心顶点是13。上一步创建的hedgehogs(刺猬)为:[4(中心),1,2,3],[6(中心),7,8,9],[5(中心),10,11,12,13]。
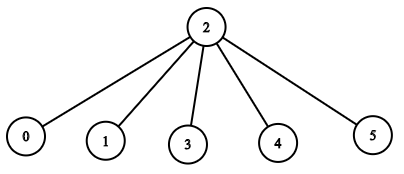
第二个例子中的树不是hedgehog,因为中心节点的度数应至少为3。
题解:
根据题意,我们构建的树,前k层都是度数 >= 3的节点,第k + 1层是度数为1的叶子节点
那我们首先找出来,这棵树是否有root节点,如果有的话,从root节点开始遍历,看每个叶子节点是否都属于k + 1层,并且非叶子节点的点,是否都有三个及以上分支
关键是确定一棵多叉树的root节点(多叉树的root节点并不等于树的重心,附上代码,第一次学)
#include <cstdio>
#include <cstring>
#include <algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
#define int long long
typedef pair<int,int> PII;
int mod = 1e9 + 7;
vector<int> p[100050];
int n,k;
int du[100050];
int vis[100050];
int root = -1;
int flag = 1,deep = -1;
void dfs(int x,int fa,int dep)
{
if(du[x] == 1)
{
if(deep == -1)
{
deep = dep;
}
else if(deep != dep)
{
flag = 0;
}
return ;
}
int cnt = 0;
for(auto ne:p[x])
{
if(fa == ne)
continue;
cnt++;
dfs(ne,x,dep + 1);
}
if(cnt < 3)
flag = 0;
}
void solve()
{
cin >> n >> k;
for(int i = 1;i < n;i++)
{
int x,y;
cin >> x >> y;
p[x].push_back(y);
p[y].push_back(x);
du[x]++;
du[y]++;
}
queue<int> q[2];
int f = 0;
for(int i = 1;i <= n;i++)
{
if(du[i] == 1)
{
vis[i] = 1;
q[f].push(i);
}
}
while(1)
{
while(q[f].size())
{
int t = q[f].front();
q[f].pop();
for(auto ne:p[t])
{
if(vis[ne])
continue;
vis[ne] = 1;
q[!f].push(ne);
}
}
f = !f;
if(q[f].size() <= 1)
{
if(q[f].size() == 1)
{
root = q[f].front();
}
else
{
root = - 1;
}
break;
}
}
if(root == -1)
{
cout <<"No";
return ;
}
dfs(root,0,0);
if(flag&&deep == k)
{
cout <<"Yes";
}
else
{
cout <<"No";
}
}
signed main()
{
// ios::sync_with_stdio(0 );
// cin.tie(0);cout.tie(0);
int t = 1;
// cin >> t;
while(t--)
{
solve();
}
}