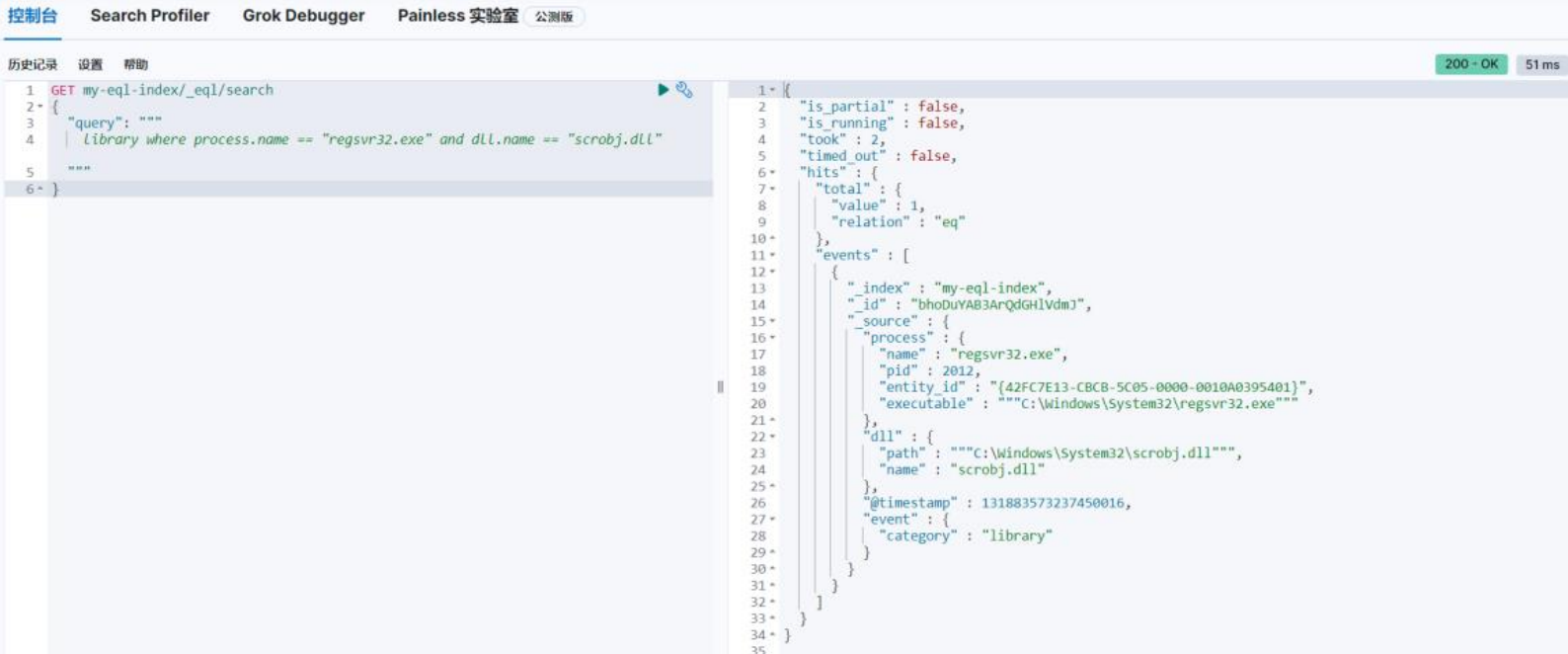
一,定义
- 对于满足以下条件的公平二人游戏,均可以用sg函数(暴搜)获得答案
- 人数2人
- 两人交替进行合法操作,无法进行者LOSE
- 对 于游戏的任意一种可能的局面,合法的操作集合只取决于这个局面的本身,而与操作者无关
- 这种游戏存在必胜点(N-Position,一定存在至少一种走法到达必败点)与必败点(P-position,不存在一种走法可以前往必胜点,处于这个位置的人必输),必败点sg值为0.
- 我们把一个点可以到达的点算入这个点的集合,那么这个集合的mex(mex函数,表示最小的不属于这个集合的非负整数,比如mex{0,1,3,4}=2,mex{1,2,3}=0.那么一个点的sg值可以成是sg(x)=mex(x)
二,sg函数打表模板
const int N = 2e5 + 10;
int dp[N],f[N];//存储sg值,f[i]存储的是i情况的状态
int n;
int sg(int x)
{
if(x<0/*x状态不合法情况*/)return dp[x]=0;//必败点
if(~dp[x])return dp[x];//已经记忆化过直接返回
set<int>mex;
for(int i=0; i<=n; ++i)
{
mex.insert(x-f[i]);//x到达i状态
}
int ans=0;
while(mex.count(ans))ans++;
return dp[x]=ans;//记忆化
}
void mysolve()
{
memset(dp,-1,sizeof(dp));
}例题一:E-小d的博弈_牛客小白月赛70 (nowcoder.com)
思路:
sg他真的没什么思路,暴搜就对了
打出来的表,挺直观的
//请按任意键继续. . .
//0 0 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
//0 0 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
//1 1 0 0 0 0 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
//1 1 0 0 0 0 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
//1 1 0 0 0 0 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
//1 1 0 0 0 0 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
//2 2 3 3 3 3 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
//2 2 3 3 3 3 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
//2 2 3 3 3 3 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
//2 2 3 3 3 3 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
//2 2 3 3 3 3 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
//2 2 3 3 3 3 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
//2 2 3 3 3 3 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
//2 2 3 3 3 3 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
//3 3 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0即不断除(1<<i++),如果除i次数相同,必败。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"
#define int long long
#define endll endl<<endl
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<long long, long long> pll;
//---------------------------------------------------------------------------------------------------------------------//
//---------------------------------------------------------------------------------------------------------------------//
//double 型memset最大127,最小128
const int INF = 0x3f3f3f3f; //int型的INF
const ll llINF = 0x3f3f3f3f3f3f3f3f;//ll型的llINF
const int N = 510;
int dp[N];
int sg(int x)
{
if(x<=0)return 0;
if(~dp[x])return dp[x];
set<int>s;
for(int i=x/2+1; i<x; ++i)s.insert(sg(x-i));
int ans=0;
while(s.count(ans))ans++;
return dp[x]=ans;
}
void mysolve()
{
//sg打表
// memset(dp,-1,sizeof(dp));
// for(int i=1; i<=30; ++i)for(int j=1; j<=30; ++j)
// {
// cout<<(sg(i)^sg(j))<<" ";
// if(j==30)cout<<endl;
// }
int x,y;
cin>>x>>y;
int l=1;
while(1)
{
x-=(1ll<<l);
y-=(1ll<<l);
if(x<=0&&y<=0)
{
cout<<"Bob"<<endl;
return;
}
else if((x>0&&y<=0)||(y>0&&x<=0))
{
cout<<"Alice"<<endl;
return;
}
l++;
}
}
int32_t main()
{
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
ll t=1;
cin >> t;
while (t--)
{
mysolve();
}
system("pause");
return 0;
}
Problem - E - Codeforces
思路:
- 容易看出可以看成是每个环的异或和,我们只需要讨论一个环的不同长度len的sg值即可
- 发现环切一次就变成链了(笑),所以我们实际只需要计算一条链不同长度的sg值即可。而一个环的长度为len的sg值,就是他第一次切后的所有可能链的sg值的集合的mex,即
- 那怎么求一条链的sg值等价于,显然一条链又可以分成两条,这两条的sg值异或和状态就是这条链可以到达的一个sg值状态。那么这条链的sg值就是
打表出来就很容易观察出每个环长度的sg值
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"
#define int long long
const int N = 2e5 + 10;
int n,l,r;
vector<int>edge[N];
bool vis[N];
int dp[N],cnt;
int sg(int x)
{
if(x<=0)return 0;
if(~dp[x])return dp[x];
set<int>s;
for(int i=l; i<=r; ++i)for(int j=0; j<=x-i; ++j)s.insert(sg(j)^sg(x-i-j));//链x的sg值对于他切掉i长度后剩余的两部分j与x-i-j的sg异或和
int ans=0;
while(s.count(ans))ans++;
return dp[x]=ans;
}
void dfs(int u)//dfs搜索一个环的节点数,即长度
{
cnt++;
vis[u]=1;
for(auto v:edge[u])if(!vis[v])dfs(v);
}
void mysolve()
{
//sg打表
// cin>>l>>r;
// memset(dp,-1,sizeof(dp));
// for(int i=1; i<=50; ++i)//求长度为i的环的sg值
// {
// set<int>s;
// for(int j=l; j<=min(r,i); ++j)s.insert(sg(i-j));//即环切掉i长度的所有sg值的mex函数
// int ans=0;
// while(s.count(ans))ans++;
// cout<<ans<<endl;
// }
cin>>n>>l>>r;
for(int i=1; i<=n; ++i)
{
if(i<l||i>(l+r-1))dp[i]=0;//打表出来的sg值规律
else dp[i]=i/l;
}
int x,y;
for(int i=1; i<=n; ++i)cin>>x>>y,edge[x].push_back(y),edge[y].push_back(x);
int ans=0;
for(int i=1; i<=n; ++i)
if(!vis[i])cnt=0,dfs(i),ans^=dp[cnt];//答案就是所有环的异或和
if(ans!=0)cout<<"Alice"<<endl;
else cout<<"Bob"<<endl;
}
int32_t main()
{
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
ll t=1;
//cin >> t;
while (t--)
{
mysolve();
}
system("pause");
return 0;
}