本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

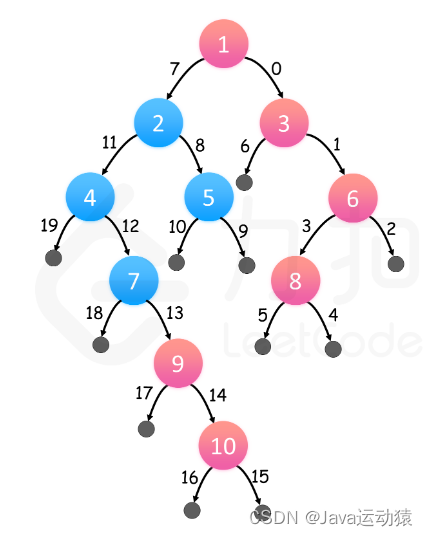
公司里有 n 名员工，每个员工的 ID 都是独一无二的，编号从 0 到 n - 1。公司的总负责人通过 headID 进行标识。

在 manager 数组中，每个员工都有一个直属负责人，其中 manager[i] 是第 i 名员工的直属负责人。对于总负责人，manager[headID] = -1。题目保证从属关系可以用树结构显示。

公司总负责人想要向公司所有员工通告一条紧急消息。他将会首先通知他的直属下属们，然后由这些下属通知他们的下属，直到所有的员工都得知这条紧急消息。

第 i 名员工需要 informTime[i] 分钟来通知它的所有直属下属（也就是说在 informTime[i] 分钟后，他的所有直属下属都可以开始传播这一消息）。

返回通知所有员工这一紧急消息所需要的 分钟数 。

示例 1：

输入：n = 1, headID = 0, manager = [-1], informTime = [0]
输出：0
解释：公司总负责人是该公司的唯一一名员工。

示例 2：

输入：n = 6, headID = 2, manager = [2,2,-1,2,2,2], informTime = [0,0,1,0,0,0]
输出：1
解释：id = 2 的员工是公司的总负责人，也是其他所有员工的直属负责人，他需要 1 分钟来通知所有员工。
上图显示了公司员工的树结构。

提示：

• 1 <= n <= 10^5
• 0 <= headID < n
• manager.length == n
• 0 <= manager[i] < n
• manager[headID] == -1
• informTime.length == n
• 0 <= informTime[i] <= 1000
• 如果员工 i 没有下属，informTime[i] == 0 。
• 题目 保证 所有员工都可以收到通知。

---

解法1 递归+自顶向下

和104. 二叉树的最大深度相似，只用把递归中的 $1$ 替换成 $\text{informTime}[x]$ ，即把 $informTime[x]$ 看做树中子树结点到儿子结点的边长。但相比二叉树，一般树需要先通过 $\text{manager}$ 数组把每个点的儿子预处理出来，存储在 $g$ 数组中。然后在递归中遍历当前节点的儿子，向下递归。

递归一般来说，有如下两种写法。有返回值的写法（自顶向下+归来时累加）：

class Solution {
	public int numOfMinutes(int n, int headID, int[] manager, int[] informTime) {
		List<Integer> g[] = new ArrayList[n];
		Arrays.setAll(g, e -> new ArrayList<>());
		for (int i = 0; i < n; ++i)
			if (manager[i] >= 0) g[manager[i]].add(i); // 建树
		return dfs(g, informTime, headID); // 从根结点headID递归，有返回值
	}
	private int dfs(List<Integer>[] g, int[] informTime, int x) {
		int maxPathSum = 0;
		for (int y : g[x]) // 遍历x的儿子y(如果没有就不会进入循环)
			maxPathSum = Math.max(maxPathSum, dfs(g, informTime, y));
		return maxPathSum + informTime[x];  // 和104题代码中return max(lDepth, rDepth) + 1;是一个意思
	}
}

传参写法（自顶向下+递去时累加）：

class Solution {
    public int numOfMinutes(int n, int headID, int[] manager, int[] informTime) {
	    List<Integer> g[] = new ArrayList[n];
	    Arrays.setAll(g, e -> new ArrayList<>());
        for (int i = 0; i < n; ++i)
            if (manager[i] >= 0)
                g[manager[i]].add(i); // 建树
        dfs(g, informTime, headID, 0); // 从根结点headID递归
        return ans;
    }
    private int ans;
    private void dfs(List<Integer>[] g, int[] informTime, int x, int pathSum) {
	    pathSum += informTime[x]; // 累加递归路径上的informTime[x]
	    ans = Math.max(ans, pathSum); // 更新答案的最大值
	    for (int y : g[x]) // 遍历x的儿子y（如果没有儿子就不会进入循环）
		    dfs(g, informTime, y, pathSum); // 继续递归
    }
}

复杂度分析：

• 时间复杂度：$\mathcal{O}(n)$ 。每个节点都恰好访问一次。
• 空间复杂度：$\mathcal{O}(n)$ 。最坏情况下，树退化成一条链，递归需要 $\mathcal{O}(n)$ 的栈空间。

---

解法二 自底向上

由于 $\text{manager}$ 数组中保存了每个节点的父节点，无需建树，直接顺着父节点，一路向上，同时累加路径上的 $\text{informTime}[x]$ 。

如果暴力枚举每个点、分别自底向上，取所有累加值中的最大值作为答案，时间复杂度是 $\mathcal{O}(n^2)$ 。如何优化？不难发现，使用 记忆化搜索 这一思想，把从 $x$ 向上得到的累加值记录到一个 $memo\text{memo}$ 数组中，如果下次再递归到 $x$ ，就直接返回 $memo$ 数组中保存的累加值（Python 可以用 @cache 装饰器）。

class Solution {
    public int numOfMinutes(int n, int headID, int[] manager, int[] informTime) {
	    var memo = new int[n];
	    Arrays.fill(memo, -1); // -1表示还没有计算过
	    int ans = 0;
	    for (int i = 0; i < n; ++i)
		    ans = Math.max(ans, dfs(manager, informTime, memo, i));
		return ans;
    }
    private int dfs(int[] manager, int[] informTime, int[] memo, int x) {
		if (manager[x] < 0) return informTime[x]; // 是根
		if (memo[x] >= 0) return memo[x]; // 之前计算过了
		return memo[x] = dfs(manager, informTime, memo, manager[x]) + informTime[x]; 
    }
}

我们可以空间优化——把计算结果直接保存到 $\text{informTime}$ 中。如何判断之前是否计算过呢？利用 $\text{manager}$ 数组，如果 $x$ 计算过，就把 $\text{manager}[x]$ 置为 $-1$ 。

class Solution {
public:
    int numOfMinutes(int n, int headID, vector<int> &manager, vector<int> &informTime) {
	    int ans = 0;
	    function<int(int)> dfs = [&](int x) -> int {
		    if (manager[x] >= 0) {
			    informTime[x] += dfs(manager[x]);
			    manager[x] = -1; // 标记x计算过
		    }
		    return informTime[x];
	    };
	    for (int i = 0; i < n; ++i) ans = max(ans, dfs(i)); 
        return ans;
    }
};

进一步地，把上面的代码改成两次迭代：

• 第一次迭代，仅累加，不更新，计算从当前节点 $i$ 往上的 $informTime$ 的累加值 $s$ 。
• 第二次迭代，更新从当前节点 $i$ 向上的每个未被计算的节点值的对应累加值。在向上移动之前，从 $s$ 中减去当前节点的 $informTime$ 值，同时设置当前节点的 $manager$ 值为 $-1$ 。

如果你学过并查集，可以试试利用这个技巧，写出 $find$ 函数的非递归版本。

class Solution {
public:
    int numOfMinutes(int n, int headID, vector<int> &manager, vector<int> &informTime) {
        int ans = 0;
        for (int i = 0; i < n; ++i) {
	        if (manager[i] < 0) continue;
	        // 计算从i向上的累加值
	        int s = 0, x = i;
	        for (; manager[x] >= 0; x = manager[x])
		        s += informTime[x];
		    // 此时x要么是headID,要么是一个计算过的结点
		    s += informTime[x];
		    ans = max(ans, s);
		    // 记录从i向上的每个未被计算的节点值的对应累加值
		    for (int x = i; manager[x] >= 0; ) {
			    int t = informTime[x];
			    informTime[x] = s;
			    s -= t;
			    int m = manager[x];
			    manager[x] = -1; // 标记已被访问
			    x = m; // 继续向上
		    }
        } 
        return ans;
    }
};

复杂度分析：

• 时间复杂度：$\mathcal{O}(n)$ 。没有建图，实际运行速度比方法一要快一些。
• 空间复杂度：$\mathcal{O}(1)$ 。仅用到若干额外变量。