全部代码

全部代码在github acwing 上
正在更新
https://github.com/stolendance/acwing
图论
欢迎star与fork

树与图的存储

无论是树 还是无向图
都可以看成有向图

有向图可以采用邻接矩阵与邻接表进行存储

邻接矩阵

邻接矩阵 采用矩阵存储,graph[i][j] 代表i到j边的权重
若之间没有边,则为INT_MAX
graph 设置成long long 以防 INT_MAX+l 变成负数
边的序号统一从1开始

typedef long long ll;
vector<vector<ll> > graph(n+1,vector<ll>(n+1,INT_MAX));
// 自己到自己为0
for(int i=1;i<n+1;i++) graph[i][i]=0;

邻接表

邻接表 每个点 用一个单链表 存储它的出边

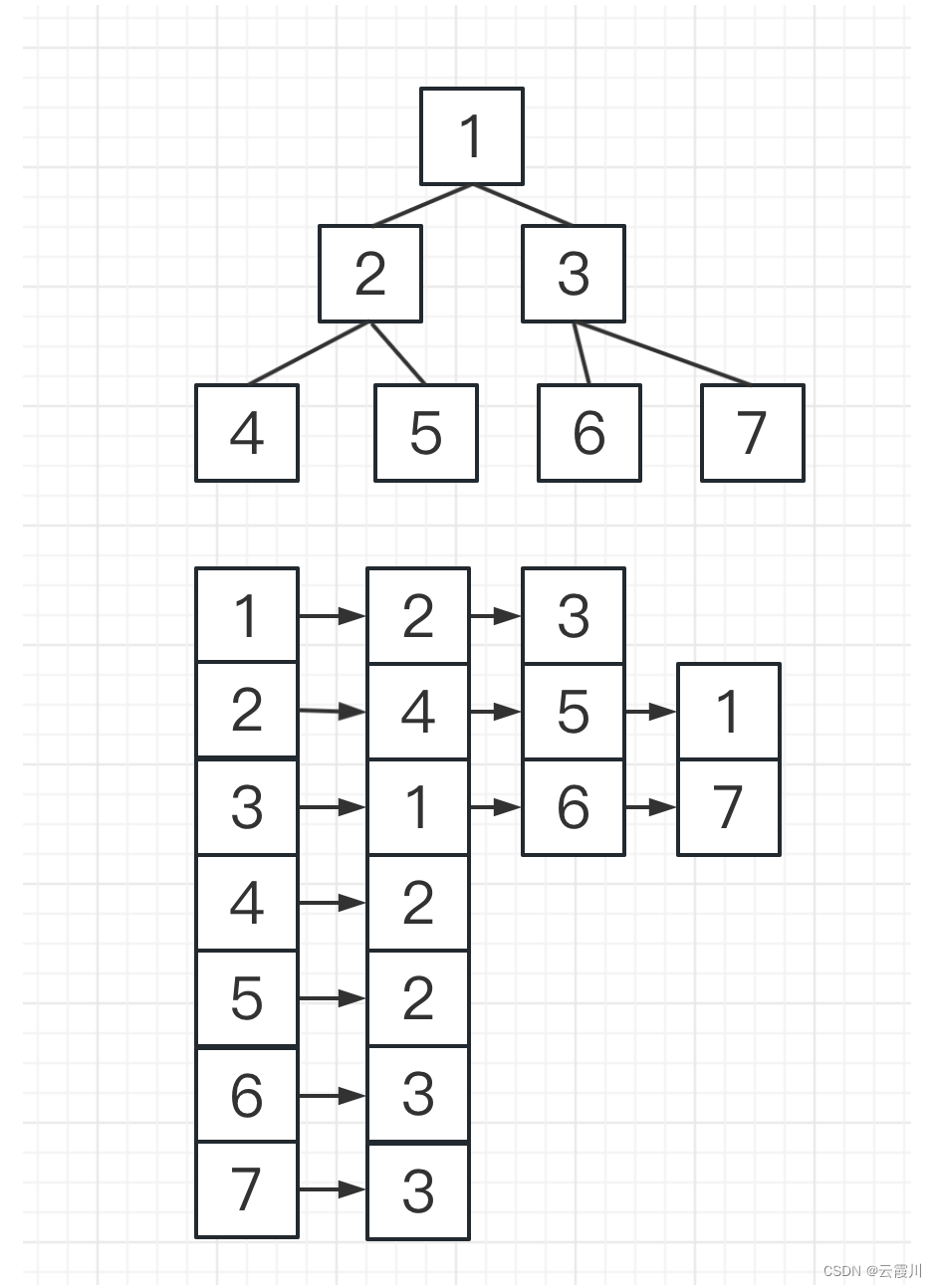
个人喜欢使用vector实现邻接表

struct Edge
{
	int next;
	int val;
	Edge(int next_,int val_):next(next_),val(val_){;}
}
vector<vector<Edge> > vec(N+1); 

加入一个边。从2指向5 权重为8
vec[2].push_back(Node(5,8));

邻接表上的深度遍历

用一个vis 数组 表示该点是否被访问过

#include<iostream>
#include<vector>
using namespace std;
struct Edge
{
    int next;
    int val;
    Edge(int next_,int val_):next(next_),val(val_){;}
};

void dfs(vector<int> &vis,vector<vector<Edge> > &vec,int u)
{
    vis[u]=1;
    for(int i=0;i<vec[u].size();i++)
    {
        if(vis[u]==0) dfs(vis,vec,vec[u][i].next);
    }
}
int main()
{
    int N=10;// 10个节点
    vector<vector<Edge> > vec(N);

    // 加入一条 5->2 的边,权重为8
    vec[5].push_back(Edge(2,8));
    vector<int> vis(N);// 代表该点是否访问过
    dfs(vis,vec,0);

}

邻接表的广度遍历

使用一个队列 依次把一个点的队列加入
按顺序访问

#include<iostream>
#include<vector>
#include<map>
#include<queue>
using namespace std;
// https://www.acwing.com/problem/content/849/
struct Edge
{
    int next;
    int value;
    Edge(int next_,int value_):next(next_),value(value_){;}
};
void bfs(vector<vector<Edge> > &graph,vector<int> &vis)
{
    queue<int> ls;
    ls.push(1);
    vis[1]=1;
    while(ls.size()!=0)
    {
        int t=ls.front();
        ls.pop();
        cout<<t<<endl;
        for(int i=0;i<graph[t].size();i++)
        {
            if(vis[graph[t][i].next]==0)
            {
                ls.push(graph[t][i].next);
                vis[graph[t][i].next]=1;
            }
        }
    }
}

int main()
{
    int n=0,m=0;
    cin>>n>>m;
    vector<vector<Edge> > graph(n+1);
    vector<int> vis(n+1);
    for(int i=0;i<m;i++)
    {
        int a,b;
        cin>>a>>b;
        graph[a].push_back(Edge(b,1));
    }
    bfs(graph,vis);
}