一、选择排序
1. 原理:
选择排序(Selection Sort)是一种简单直观的排序算法,它的基本思路是将数组按顺序分成已排序部分和未排序部分,然后每次从未排序部分中选择出最小的元素,将其添加到已排序部分的末尾。重复这个过程,直到未排序部分为空,整个数组都已排好序。
2. 代码
def selection_sort(lst):
n = len(lst)
for i in range(n):
min_idx = i
for j in range(i+1, n):
if lst[j] < lst[min_idx]:
min_idx = j
lst[i], lst[min_idx] = lst[min_idx], lst[i]
return lst
arr = [3, 5, 8, 1, 2, 9, 4, 7, 6]
sorted_arr = selection_sort(arr)
print(sorted_arr)
二、冒泡排序
1. 原理:
冒泡排序(Bubble Sort)是一种简单直观的排序算法,它的基本思路是重复地遍历数列,一次比较两个元素,如果它们的顺序错误,就交换位置。每一次遍历都将最大或最小的元素“浮”到了最顶端,因此得名冒泡排序。
2. 代码
def bubble_sort(lst):
n = len(lst)
for i in range(n-1):
for j in range(n-i-1):
if lst[j] > lst[j+1]:
lst[j], lst[j+1] = lst[j+1], lst[j]
return lst
lst = [8, 3, 5, 1, 2, 7, 6, 4]
sorted_lst = bubble_sort(lst)
print(sorted_lst) # 输出 [1, 2, 3, 4, 5, 6, 7, 8]
三、插入排序
1. 原理:
插入排序(Insertion Sort)是一种简单直观的排序算法,它的基本思路是将未排序的元素一个一个插入到已经排序的部分中适当的位置上去。它的实现过程是将一个待排序的列表分成两部分,第一部分为已排序的,第二部分为未排序的,初始状态下第一部分为列表中的第一个元素,而第二部分为除第一个元素外的其他元素。在排序过程中,我们是从未排序部分中取出一个元素,将它插入到已排序部分中去。重复这个过程,直到未排序部分为空,整个列表都已排好序。
2. 代码
def insertion_sort(lst):
n = len(lst)
for i in range(1, n):
key = lst[i]
j = i - 1
while j >= 0 and lst[j] > key:
lst[j+1] = lst[j]
j -= 1
lst[j+1] = key
return lst
lst = [8, 3, 5, 1, 2, 7, 6, 4]
sorted_lst = insertion_sort(lst)
print(sorted_lst) # 输出 [1, 2, 3, 4, 5, 6, 7, 8]
该函数的主要实现过程如下:
- 遍历整个列表,从下标 i=1 开始,逐步将未排序部分添加到已排序部分中
- 选取未排序部分的第一个元素作为 key,将其与已排序部分逐一比较
- 如果 key 小于已排序部分的某一个元素,则将该元素向后移动一位,继续比较
- 如果 key 大于或等于已排序部分的某一个元素,则将 key 插入到该元素后面
四、归并排序
1. 原理:
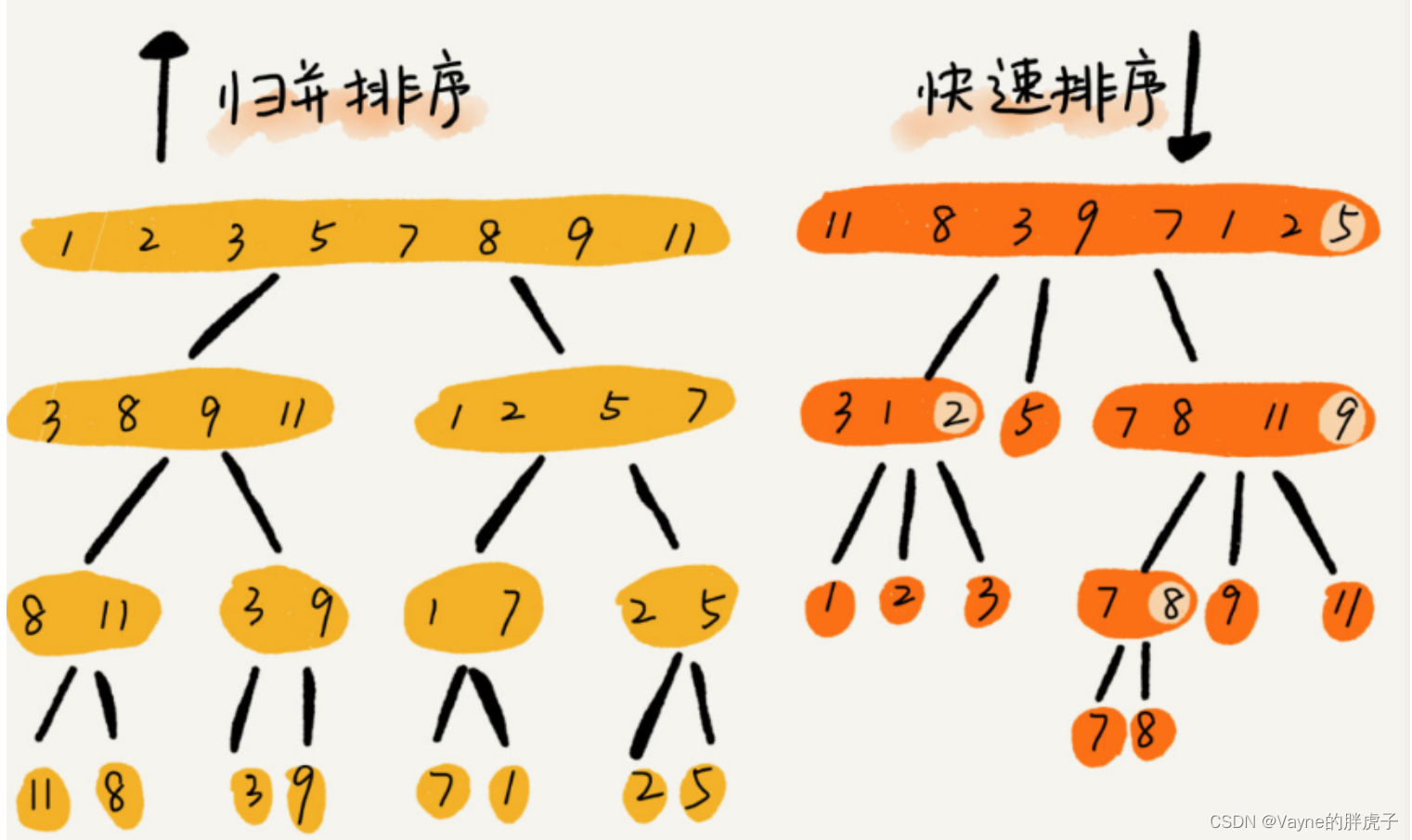
归并排序(Merge Sort)是一种基于分治思想的排序算法,它的基本思路是将数组分成两个等长的部分,分别对这两部分进行递归排序,然后将排好序的两个子数组合并起来。因为归并排序的实现过程中需要开辟额外的空间来存储临时数组,所以归并排序不是基于比较排序的最优算法,但归并排序的时间复杂度通常很优秀,表现稳定。
2. 代码
def merge_sort(arr):
# 递归终止条件,数组长度为 1
if len(arr) == 1:
return arr
# 将数组一分为二,并递归对两个子数组进行排序
mid = len(arr) // 2
left = merge_sort(arr[:mid])
right = merge_sort(arr[mid:])
# 对排好序的子数组进行归并操作
sorted_arr = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
sorted_arr.append(left[i])
i += 1
else:
sorted_arr.append(right[j])
j += 1
sorted_arr += left[i:]
sorted_arr += right[j:]
return sorted_arr
lst = [8, 3, 5, 1, 2, 7, 6, 4]
sorted_lst = merge_sort(lst)
print(sorted_lst) # 输出 [1, 2, 3, 4, 5, 6, 7, 8]
该函数的主要实现过程如下:
- 如果数组长度为 1,直接返回该数组(递归终止条件)
- 将数组一分为二,并递归对左右两个子数组进行排序,最终返回排好序的子数组
- 对排好序的子数组进行归并操作,通过比较两个子数组的首元素,不断将更小的元素添加到一个新的数组中,最终将子数组中剩余的元素也加入到新数组中来
- 返回归并后的新数组
五、快速排序
1. 原理
快速排序是一种基于分治思想的排序算法,它的基本思路是先找到一个基准值(pivot),将数组划分为两部分,使得左半部分的所有元素小于等于基准值,右半部分的所有元素大于基准值。然后对左右两个部分分别递归地进行同样的处理,直到整个数组有序。
2. 代码
def quick_sort(arr):
# 如果数组长度小于等于 1,直接返回
if len(arr) <= 1:
return arr
# 选择第一个元素为基准值,随机选择也是一种优化方法
pivot = arr[0]
# 使用列表推导式获取左侧和右侧子数组
left = [x for x in arr[1:] if x <= pivot]
right = [x for x in arr[1:] if x > pivot]
# 递归调用快速排序,并将左右子数组拼接起来
return quick_sort(left) + [pivot] + quick_sort(right)
lst = [8, 3, 5, 1, 2, 7, 6, 4]
sorted_lst = quick_sort(lst)
print(sorted_lst) # 输出 [1, 2, 3, 4, 5, 6, 7, 8]
该函数的实现并不复杂,思路也比较清晰。主要包含以下步骤:
- 如果数组长度小于等于 1,直接返回该数组
- 选择第一个元素作为基准值,将数组划分为左右两个子数组,分别为左半部分 left 和右半部分 right
- 对左右子数组进行递归调用快速排序,并将将子数组返回值拼接成新数组,注意需要将基准值 pivot 放入中间
六、堆排序
1. 原理
在 heapify() 函数中,函数的参数 n 表示构成二叉树的前 n 个元素,参数 i 表示当前根节点在数组中的位置。该函数的作用是将以 i 为根节点的子树进行堆化,也就是将其变成一个最大堆。在实现过程中,需要不断检查左右子节点和根节点之间的大小关系,并进行必要的交换。
heap_sort() 函数中,先使用叶节点的父节点开始建立一个最大堆,然后对于数组中已经是最大堆的部分,每次提取根节点(最大值),并将其与堆结构末尾的值进行交换。整个排序过程时间复杂度为 O(nlogn)。
2. 代码
def heapify(arr, n, i):
"""
以 i 为根节点,将 arr 中的前 n 个元素构成的二叉树进行堆化
"""
largest = i
left = 2 * i + 1
right = 2 * i + 2
# 寻找最大值节点
if left < n and arr[left] > arr[largest]:
largest = left
if right < n and arr[right] > arr[largest]:
largest = right
# 如果最大值节点不是 i,那么需要进行交换
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
# 递归堆化交换后的子树
heapify(arr, n, largest)
def heap_sort(arr):
n = len(arr)
# 构建最大堆
for i in range(n//2 - 1, -1, -1):
heapify(arr, n, i)
# 逐个取出最大值
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i]
# 对前 i 个元素进行重新构建最大堆
heapify(arr, i, 0)
return arr
lst = [8, 3, 5, 1, 2, 7, 6, 4]
sorted_lst = heap_sort(lst)
print(sorted_lst) # 输出 [1, 2, 3, 4, 5, 6, 7, 8]