【状态机dp之 股票买卖 题型系列 帮你学懂 状态机】股票买卖（1-6道题）

news2024/9/21 2:42:19

股票买卖

        • 股票买卖 1
            • 这道题就是求max {ai−aj|j<i}
        • 股票买卖 2
        • 股票买卖 3
            • 方法一：前后缀拆分dp
            • 怎么想到的？
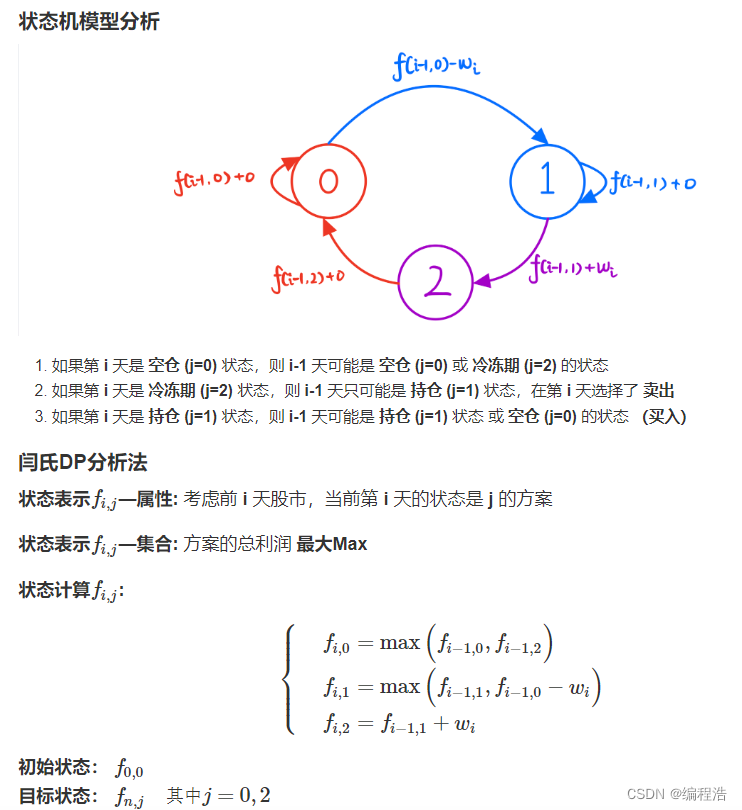
            • 方法二：状态机dp
            • f[0/1][i]表示只考虑前i支股票且手头有/没有股票的最大收益
        • 股票买卖 4
            • 考虑前 i 天的股票，第 i 天的 决策 是 k，且完成的 完整交易数 为 j 的方案
        • 股票买卖 5
        • 股票买卖 6

股票买卖 1

原题链接

这道题就是求max {ai−aj|j<i}
#include<iostream>

using namespace std;

const int N = 1e5+10;

int a[N];
int n;
int mi = 0x3f3f3f3f;
int ans = 0;

int main()
{
    
    cin >> n;
    
    for(int i = 1; i <= n; i++)
    {
        cin >> a[i];
        
        mi = min(a[i],mi);
        
        if(i!=1)
        {
            ans = max(ans,a[i]-mi);
        }
        
    }
    
    cout << ans;
    
    return 0;
}

股票买卖 2

原题链接

#include<iostream>

using namespace std;

const int N = 1e5+10;

int a[N];

int n;

int main()
{
    cin >> n;
    
    int ans = 0;
    
    for(int i = 1; i <= n; i++)
    {
        cin >> a[i];
        if(i!=1)
            ans = ans + max(0,a[i]-a[i-1]);
    }
    
    cout << ans;
    
    return 0;
}

股票买卖 3

方法一：前后缀拆分dp
怎么想到的？

首先我们想的是，先按着第一道题的方法，遍历一边数组，得到买卖一次的最大值，然后再遍历一次，得到买卖第二次的最大值，但是这个是不行的。
原因是，这道题要求我们，第二次买之前，第一次的必须卖出去

所以，我们想到的是开两个dp数组

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;
int arr[N];

int dp[N];
int rdp[N];

int n;

int main()
{
    cin >> n;

    for (int i = 0; i < n; i++) {
        cin >> arr[i];
    }
    int low = 9999999;
    int ans = 0;
    for (int i = 0; i < n; i++) {
        low = min(low, arr[i]);
        ans = max(ans, arr[i] - low);
        dp[i] = ans;
    }

    int high = 0;
    ans = 0;
    for (int i = n - 1; i >= 0; i--) {
        high = max(high, arr[i]);
        ans = max(ans, high - arr[i]);
        rdp[i] = ans;
    }
    ans = 0;
    for (int i = 0; i < n; i++) {
        ans = max(ans,dp[i] + rdp[i]);
    }
    cout << ans << endl;


    return 0;
}
方法二：状态机dp
f[0/1][i]表示只考虑前i支股票且手头有/没有股票的最大收益

在这里插入图片描述

#include<iostream>
#include<cstdio>
#include<cstring>
typedef long long ll;
#define MAXN 200011
ll f[5][MAXN];
int main()
{
    memset(f,0xcf,sizeof f);
    ll n;
    scanf("%lld",&n);
    f[0][0]=0;
    for(ll i=1;i<=n;++i)
    {
        ll x;
        scanf("%lld",&x);
        f[0][i]=f[0][i-1];
        f[1][i]=std::max(f[1][i-1],f[0][i-1]-x);
        f[2][i]=std::max(f[2][i-1],f[1][i-1]+x);
        f[3][i]=std::max(f[3][i-1],f[2][i-1]-x);
        f[4][i]=std::max(f[4][i-1],f[3][i-1]+x);
    }
    printf("%lld",std::max(f[0][n],std::max(f[2][n],f[4][n])));
    return 0;
}

股票买卖 4

在这里插入图片描述

原题链接

考虑前 i 天的股票，第 i 天的 决策 是 k，且完成的 完整交易数 为 j 的方案
#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e5 + 10, M = 110;

int n, k;
int w[N];
int f[N][M][2];

int main()
{
    cin >> n >> k;
    for (int i = 1; i <= n; ++ i) cin >> w[i];

    memset(f, -0x3f, sizeof f);
    f[0][0][0] = 0; //初始状态f[0][0][0]

    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 0; j <= k; ++ j)
        {
            f[i][j][0] = f[i - 1][j][0];
            if (j) f[i][j][0] = max(f[i][j][0], f[i - 1][j - 1][1] + w[i]);
            f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j][0] - w[i]);
        }
    }

    int res = 0;
    for (int j = 0; j <= k; ++ j) res = max(res, f[n][j][0]); //目标状态f[n][j][0]

    cout << res << endl;

    return 0;
}

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e5 + 10, M = 110;

int n, k;
int w[N];
int f[2][M][2];

int main()
{
    cin >> n >> k;
    for (int i = 1; i <= n; ++ i) cin >> w[i];

    memset(f, -0x3f, sizeof f);
    f[0][0][0] = 0; //初始状态f[0][0][0]

    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 0; j <= k; ++ j)
        {
            f[i & 1][j][0] = f[(i - 1) & 1][j][0];
            if (j) f[i & 1][j][0] = max(f[i & 1][j][0], f[(i - 1) & 1][j - 1][1] + w[i]);
            f[i & 1][j][1] = max(f[(i - 1) & 1][j][1], f[(i - 1) & 1][j][0] - w[i]);
        }
    }

    int res = 0;
    for (int j = 0; j <= k; ++ j) res = max(res, f[n & 1][j][0]); //目标状态f[n][j][0]

    cout << res << endl;

    return 0;
}

股票买卖 5

在这里插入图片描述

在这里插入图片描述

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e5 + 10, M = 110;

int n, k;
int w[N];
int f[N][M][2];

int main()
{
    cin >> n >> k;
    for (int i = 1; i <= n; ++ i) cin >> w[i];

    memset(f, -0x3f, sizeof f);
    f[0][0][0] = 0; //初始状态f[0][0][0]

    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 0; j <= k; ++ j)
        {
            f[i][j][0] = f[i - 1][j][0];
            if (j) f[i][j][0] = max(f[i][j][0], f[i - 1][j - 1][1] + w[i]);
            f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j][0] - w[i]);
        }
    }

    int res = 0;
    for (int j = 0; j <= k; ++ j) res = max(res, f[n][j][0]); //目标状态f[n][j][0]

    cout << res << endl;

    return 0;
}

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e5 + 10, M = 110;

int n, k;
int w[N];
int f[2][M][2];

int main()
{
    cin >> n >> k;
    for (int i = 1; i <= n; ++ i) cin >> w[i];

    memset(f, -0x3f, sizeof f);
    f[0][0][0] = 0; //初始状态f[0][0][0]

    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 0; j <= k; ++ j)
        {
            f[i & 1][j][0] = f[(i - 1) & 1][j][0];
            if (j) f[i & 1][j][0] = max(f[i & 1][j][0], f[(i - 1) & 1][j - 1][1] + w[i]);
            f[i & 1][j][1] = max(f[(i - 1) & 1][j][1], f[(i - 1) & 1][j][0] - w[i]);
        }
    }

    int res = 0;
    for (int j = 0; j <= k; ++ j) res = max(res, f[n & 1][j][0]); //目标状态f[n][j][0]

    cout << res << endl;

    return 0;
}

作者：一只野生彩色铅笔
链接：https://www.acwing.com/solution/content/55037/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

股票买卖 6

原题链接
在这里插入图片描述

#include <iostream>

const int N=100010;

int n,f;
int data[N];
int dp[2][N];

int main()
{
    scanf("%d %d\n",&n,&f);
    for(int i=1;i<=n;i++)
        scanf("%d",&data[i]);
    dp[1][1]=-data[1];
    for(int i=2;i<=n;i++)
    {
        dp[0][i]=std::max(dp[0][i-1],data[i]+dp[1][i-1]-f);
        dp[1][i]=std::max(dp[1][i-1],dp[0][i-1]-data[i]);
    }
    std::cout<<dp[0][n];
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/480873.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

深入浅出C++ ——C++11

深入浅出C++ ——C++11

文章目录 一、C11简介二、列表初始化二、声明四、范围for循环五、STL中的变化六、右值引用和移动语义1. 什么是左值&#xff1f;什么是左值引用&#xff1f;2. 左值引用与右值引用比较3. 右值引用使用场景和意义4. 完美转发 新的类功能默认成员函数类成员变量初始化defaultdele…
阅读更多...
在Unity中制作完整的技能系统（介绍篇）

在Unity中制作完整的技能系统（介绍篇）

1. 系统结构介绍 首先我们需要对技能中的部分进行一个划分。通过观察&#xff0c;我们不难发现&#xff0c;在多个技能中经常有一些相同的内容&#xff08;以下的例子均来自于《英雄联盟》&#xff09;&#xff1a; 火男被动的燃烧一定时间持续伤害和提莫的E技能中毒一定时间…
阅读更多...
【@Param注解】| 台面使用——＞底层原理分析

【@Param注解】| 台面使用——＞底层原理分析

🐇 🐇 😄 🐇 🐇 🐇 🐇 😄 🐇 🐇 🐇 🐇 😄 🐇 🐇 🐇 🐇 😄 🐇 🐇 🐇 🐇 😄 目录 🦁 定义🦁 台面使用🦁 底层原理分析🦁 尾声🐇 🐇 😄 🐇 🐇 🐇 🐇 😄 🐇 🐇 🐇 🐇 😄 🐇 🐇 🐇 🐇 😄…
阅读更多...
【Python】什么是爬虫，爬虫实例

【Python】什么是爬虫，爬虫实例

有s表示加密的访问方式 一、初识爬虫 什么是爬虫 网络爬虫&#xff0c;是一种按照一定规则&#xff0c;自动抓取互联网信息的程序或者脚本。由于互联网数据的多样性和资源的有限性&#xff0c;根据用户需求定向抓取相关网页并分析已成为如今主流的爬取策略爬虫可以做什么 你可以…
阅读更多...
【JAVAEE】JAVA数据库连接（JDBC）

【JAVAEE】JAVA数据库连接（JDBC）

1.什么是JDBC&#xff1f; Java数据库连接&#xff0c;&#xff08;Java Database Connectivity&#xff0c;简称JDBC&#xff09;是Java语言中用来规范客户端程序如何来访问数据库的应用程序接口&#xff0c;提供了诸如查询和更新数据库中数据的方法。JDBC也是Sun Microsyste…
阅读更多...
[优雅的面试]MySQL与Redis双写一致性方案

[优雅的面试]MySQL与Redis双写一致性方案

前言 由于缓存的高并发和高性能已经在各种项目中被广泛使用&#xff0c;在读取缓存这方面基本都是一致的&#xff0c;大概都是按照下图的流程进行操作&#xff1a; 但是在更新缓存方面&#xff0c;是更新完数据库再更新缓存还是直接删除缓存呢&#xff1f;又或者是先删除缓存再…
阅读更多...
TypeError: Object of type ‘Decimal‘ is not JSON serializable

TypeError: Object of type ‘Decimal‘ is not JSON serializable

错误 TypeError: Object of type ‘Decimal’ is not JSON serializable 场景 该错误是在Python3中使用Flask的报错&#xff0c;之前代码是运行正常的&#xff0c;时过几年后再次安装部署&#xff0c;确出现问题。 分析 经过分析发现依旧是版本依赖导致的更新问题。最近在…
阅读更多...
JS手写实现Promise.race

JS手写实现Promise.race

Promise.race() 是一个常见的 JavaScript Promise 方法&#xff0c;它接受一个 Promise 数组作为参数&#xff0c;并返回一个新的 Promise 对象。这个新的 Promise 对象在传入的 Promise 数组中&#xff0c;任意一个 Promise 对象状态变为 fulfilled 或者 rejected&#xff0c;…
阅读更多...
57.网页设计图标实战

57.网页设计图标实战

首先我们需要找一个图标库&#xff0c;本次演示采用的是heroicon ● 之后我们根据需求搜索与之想匹配的图标并复制svg代码 ● 之后将我们的代码复制到我们想要放置图标的地方 ● 当然我们需要使用CSS来修饰一下 .features-icon {stroke: #087f5b;width: 32px;height: 3…
阅读更多...
Python——Pyqt5的数据可视化小工具（完整代码）

Python——Pyqt5的数据可视化小工具（完整代码）

前言 作业要求&#xff1a;【都已经打包放网上了&#xff0c;有缘人需要就自取】 一份报告书&#xff08;在全球变暖背景下碳中和对各国的二氧化碳排放量的影响项目报告书&#xff09; 一份代码 作业包&#xff1a;python数据可视化小工具.zip - 蓝奏云 大一的时候&#xff0c;…
阅读更多...
Java 整合常用docker Api

Java 整合常用docker Api

整合环境&#xff1a; 与docker 版本差异不大&#xff0c;基本都可以 API version: 1.26开放docker api &#xff0c;两种方式 /etc/sysconfig/docker &#xff0c;最后一行添加&#xff1b;开放端口&#xff1a;2375 -H tcp://0.0.0.0:2375systemctl status docker 查询 d…
阅读更多...
vsftpd.conf参数配置

vsftpd.conf参数配置

文章目录 初始vsftdp.conf翻译后需修改参数write_enableYES&#xff08;启用任何形式的FTP写入命令&#xff09;userlist_file/etc/vsftpd.user_list、userlist_enableYES、userlist_denyNOlocal_umask022&#xff08;放开权限&#xff09;chroot_local_userYES&#xff08;限定…
阅读更多...
每日学术速递4.29

每日学术速递4.29

CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.LG 1.A Cookbook of Self-Supervised Learning 标题&#xff1a;自监督学习食谱 作者&#xff1a;Randall Balestriero, Mark Ibrahim, Vlad Sobal, Ari Morcos, Shashank Shekhar, Tom…
阅读更多...
学知识变现，看完这些就够了

学知识变现，看完这些就够了

点击查看【18本知识变现电子书】 100个实用知识点 60万字知识变现精华 资深知识变现教练海哥扛鼎之作 2000多位学员实战经验干货总结 从理论到实践&#xff0c;从思维到实操 教你彻底学透如何知识变财富 .......... 全网最全知识变现知识付费电子教程 资深知识变现教练海…
阅读更多...
Linux线程相关函数：线程的创建、属性、回收、退出、取消

Linux线程相关函数：线程的创建、属性、回收、退出、取消

1. 线程号 进程号在系统中唯一&#xff0c;但线程号只在其所属进程环境中有效。 &#xff08;1&#xff09;pthread_self函数 #include<pthread.h>pthread_t pthread_self(void); /* 功能&#xff1a;获取线程号 返回值&#xff1a;调用此函数线程的ID */ pthread_se…
阅读更多...
【Unity-UGUI控件全面解析】| Panel 容器组件详解

【Unity-UGUI控件全面解析】| Panel 容器组件详解

🎬【Unity-UGUI控件全面解析】| Panel 容器组件详解一、组件介绍二、组件属性面板三、代码操作组件💯总结🎬 博客主页：https://xiaoy.blog.csdn.net 🎥 本文由 呆呆敲代码的小Y 原创，首发于 CSDN🙉 🎄 学习专栏推荐：Unity系统学习专栏 🌲 游戏制作专栏推荐：游…
阅读更多...
2007-2020年上市公司数字经济化指标含原始数据和计算代码（do文档）

2007-2020年上市公司数字经济化指标含原始数据和计算代码（do文档）

2007-2020年上市公司数字经济化指标含原始数据和计算代码&#xff08;do文档&#xff09; 1、时间&#xff1a;2007-2020 2、范围&#xff1a;A股上市公司剔除jin rong行业 3、数据说明&#xff1a;包含计算过程和原始数据 4、参考文献&#xff1a;祁怀锦,数字经济对公司治…
阅读更多...
利用C#实现动态替换桌面快捷方式对应的应用程序

利用C#实现动态替换桌面快捷方式对应的应用程序

公司有一个特殊的业务可能会用到这个&#xff0c;至于什么业务就不展开了。本文的内容作为备用方案。 实现思路&#xff1a; 1 获取当前exe程序运行的全路径 2 获取桌面的所有快捷方式 3 遍历快捷方式&#xff0c;获取快捷键方式对应程序的运行路径&#xff0c;并与当前…
阅读更多...
【开发工具】 今天我要教会你安装Office 2021 RTM 专业增强零售版 你开不开心

【开发工具】 今天我要教会你安装Office 2021 RTM 专业增强零售版 你开不开心

&#x1f680; 个人主页 极客小俊 ✍&#x1f3fb; 作者简介&#xff1a;web开发者、设计师、技术分享博主 &#x1f40b; 希望大家多多支持一下, 我们一起进步&#xff01;&#x1f604; &#x1f3c5; 如果文章对你有帮助的话&#xff0c;欢迎评论 &#x1f4ac;点赞&#x1…
阅读更多...
统一请求封装和pytest入门使用

统一请求封装和pytest入门使用

统一请求封装解决的问题 解决多个py文件共享session的问题 统计请求的数据 统一异常处理 统一日志监控 封装 在项目文件中创建一个common文件夹&#xff0c; 用来进行统一接口封装 import requestsclass RequestUtil:# 调用底层的requests.session()方法进行封装sess r…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023